Areas of Sector and Segment of a Circle
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Sectors and Segments
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will explore sectors and segments of circles. A sector is part of a circle enclosed by two radii. Who can tell me what a segment is?

Isn't a segment the area between a chord and the arc?

Exactly! We have minor segments and major segments. The minor segment is smaller than half the circle. Remember: S for Sector and S for Segment, but they are quite different!

What about the angles? Are there specific angles for minor and major?

Great question! The angle of a major sector can be calculated as 360° minus the minor sector angle. Let's imagine a pizza: cut right down the middle gives us a slice!
Calculating Area of a Sector
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's learn how to find the area of a sector. The formula is given by the relation. Can someone tell me what it is?

Is it \(\frac{\theta}{360} \times \pi r^2\)?

Exactly! If \(\theta\) is the angle at the center, we use this formula. Let's break this down: it helps us find out how much of the entire circle we are considering based on the angle.

How do we calculate it practically?

Let’s work through an example together! If the radius is 4 cm and the angle is 30°, we calculate it as \(\frac{30}{360} \times \pi \times 4^2\).
Finding the Area of a Segment
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let’s delve into finding the area of a segment. Does anyone remember how we derived its area?

It’s the area of the sector minus the area of the triangle, right?

Correct! So, if we have a segment with the same radius of 4 cm and angle of 30°, we’ll need to calculate the area of the triangle. What’s the formula for that?

The area of a triangle is \(\frac{1}{2} \times base \times height\).

Well done! The combination of those calculates the area of the segment.
Practical Applications and Problem Solving
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's apply the concepts learned through a real-life example! If a clock's minute hand sweeps through a certain angle, can anyone tell me how we can calculate the area it sweeps?

Could we use the sector area formula with the angle the minute hand covers?

Absolutely! Excellent job! Let’s plug in the values and do the calculation together for, say, a hand of length 14 cm sweeping over 30°.

This is really helping me visualize how these calculations work in real life!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, students learn to differentiate between sectors and segments of circles, understand how to calculate their areas using specific formulas, and apply these concepts through illustrative examples and exercises.
Detailed
Areas of Sector and Segment of a Circle
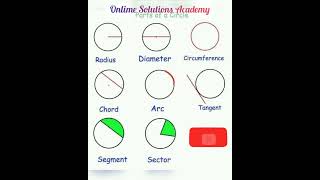
In this section, we analyze the concepts of sectors and segments within circles, which are vital in understanding circular areas. A sector is defined as the portion of a circle enclosed by two radii and the respective arc. Conversely, a segment lies between a chord and the arc corresponding to that chord.
Key Concepts:
- Minor and Major Sectors: The smaller sector formed is called the minor sector, while the larger one is referred to as the major sector. The angle of the major sector is defined as the total circle (360°) minus the angle of the minor sector.
- Calculating the Area of a Sector: The area can be calculated by the formula:
$$\text{Area of sector} = \frac{\theta}{360} \times \pi r^2$$
where \(\theta\) is the angle at the center in degrees and \(r\) is the radius.
- Arc Length: The formula for the arc length is:
$$\text{Length of arc} = \frac{\theta}{360} \times 2\pi r$$
- Segments of a Circle: The area of a segment is derived by subtracting the area of the associated triangle (formed by the radii and the chord) from the area of the sector.
$$\text{Area of segment} = \text{Area of sector} - \text{Area of triangle}$$
Practical Examples and Exercises:
Through examples and exercises, students reinforce their understanding by calculating areas for given sectors and segments under different scenarios, solidifying their grasp on circular areas.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Sectors and Segments
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
You have already come across the terms sector and segment of a circle in your earlier classes. Recall that the portion (or part) of the circular region enclosed by two radii and the corresponding arc is called a sector of the circle and the portion (or part) of the circular region enclosed between a chord and the corresponding arc is called a segment of the circle. Thus, in Fig. 11.1, shaded region OAPB is a sector of the circle with centre O. ∠ AOB is called the angle of the sector. Note that in this figure, unshaded region OAQB is also a sector of the circle. For obvious reasons, OAPB is called the minor sector and OAQB is called the major sector. You can also see that angle of the major sector is 360° – ∠ AOB.
Detailed Explanation
In this chunk, we learn about two important parts of circles: sectors and segments. A sector is like a slice of pizza; it's the area enclosed by two radii (the edges of the slice) and the arc (the crust). A segment is more like a piece of a pizza that is restricted by a straight line (the chord) and the arc above that line. In the context of this definition, 'minor' refers to the smaller part (minor sector/segment) while 'major' refers to the larger part (major sector/segment). Understanding these definitions sets the groundwork for calculating areas.
Examples & Analogies
Think of a birthday cake. If you take a slice (that’s the sector), it consists of the crust and the pieces of the cake (the area between the two radii). If you take a piece that’s above a partition line and below the crust (like some toppings), that’s a segment. It’s helpful to understand these concepts with everyday objects like cakes, pizzas, or even segments of fruit.
Area of a Sector of a Circle
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now with this knowledge, let us try to find some relations (or formulae) to calculate their areas. Let OAPB be a sector of a circle with centre O and radius r (see Fig. 11.3). Let the degree measure of ∠AOB be θ. You know that area of a circle (in fact of a circular region or disc) is πr². In a way, we can consider this circular region to be a sector forming an angle of 360° (i.e., of degree measure 360) at the centre O. Now by applying the Unitary Method, we can arrive at the area of the sector OAPB as follows: When degree measure of the angle at the centre is 360, area of the sector = πr². When the degree measure of the angle at the centre is 1, area of the sector = πr²/360. Therefore, when the degree measure of the angle at the centre is θ, area of the sector = (θ/360) * πr². Thus, we obtain the following relation (or formula) for area of a sector of a circle: Area of the sector of angle θ = (θ/360) * πr².
Detailed Explanation
Here, we derive the formula to calculate the area of a sector of a circle. The full circle has an area of πr², proportional to the angle subtended at the center. To find the area for a sector with an angle θ instead of 360°, we multiply the full area by the fraction of θ/360. This gives us a reliable way to calculate the area of any sector as long as we know the radius and the angle.
Examples & Analogies
Imagine you have a pie that represents a full circle and it can be cut into 360 slices. If you only take one slice (1 degree), it would represent a tiny fraction of the total area. Now, if you take 30 slices (30 degrees), to find out how much area that is, you'd need to calculate the fraction of the total pie that your 30 slices represent. This is exactly how the formula works!
Length of an Arc
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now a natural question arises: Can we find the length of the arc APB corresponding to this sector? Yes. Again, by applying the Unitary Method and taking the whole length of the circle (of angle 360°) as 2πr, we can obtain the required length of the arc APB as (θ/360) * 2πr.
Detailed Explanation
Similar to how we found the area of the sector, we can find the length of the arc relating to a specific angle. The entire circumference of a circle is 2πr, but if we're looking for just a segment of that, we again apply the fraction represented by θ/360 to find the length of the arc for any angle θ.
Examples & Analogies
Think of a circular race track. If the entire length around the track (full circle) is the distance all the way around (2πr), then if you only run 90 degrees (a quarter of the race), the distance you ran is a quarter of the whole length. This same principle applies to calculating arc lengths; you merely multiply the total length by the fraction you've covered.
Area of a Segment of a Circle
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now let us take the case of the area of the segment APB of a circle with centre O and radius r. You can see that: Area of the segment APB = Area of the sector OAPB – Area of ΔOAB = (θ/360) * πr² – Area of ΔOAB. Note: From Fig. 11.3 and Fig. 11.4 respectively, you can observe the Area of the major sector OAQB = πr² – Area of the minor sector OAPB and Area of major segment AQB = πr² – Area of the minor segment APB.
Detailed Explanation
The area of the segment is derived from subtracting the area of the triangle formed by the radii and the chord from the area of the sector. Essentially, it tells us how much area is enclosed between the arc and the chord, highlighting the importance of both components in calculating areas of segments.
Examples & Analogies
Let's use the pizza analogy again. If you have a slice of pizza (the sector) and you remove the triangular part of that slice that formed by the crust and the two cuts (the triangle), what remains is the segment, the part that is delicious but lacks the simple triangle shape. This analogy helps visualize how segments relate to sectors.
Key Concepts
-
Minor and Major Sectors: The smaller sector formed is called the minor sector, while the larger one is referred to as the major sector. The angle of the major sector is defined as the total circle (360°) minus the angle of the minor sector.
-
Calculating the Area of a Sector: The area can be calculated by the formula:
-
$$\text{Area of sector} = \frac{\theta}{360} \times \pi r^2$$
-
where \(\theta\) is the angle at the center in degrees and \(r\) is the radius.
-
Arc Length: The formula for the arc length is:
-
$$\text{Length of arc} = \frac{\theta}{360} \times 2\pi r$$
-
Segments of a Circle: The area of a segment is derived by subtracting the area of the associated triangle (formed by the radii and the chord) from the area of the sector.
-
$$\text{Area of segment} = \text{Area of sector} - \text{Area of triangle}$$
-
Practical Examples and Exercises:
-
Through examples and exercises, students reinforce their understanding by calculating areas for given sectors and segments under different scenarios, solidifying their grasp on circular areas.
Examples & Applications
Example: Find the area of a sector with radius 4 cm and angle 30°: Area = \(\frac{30}{360} \times \pi (4^2) \approx 4.19 cm^2\).
Example: Calculate the area of a segment formed in a circle with radius 21 cm and angle 120°.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
A circle's sector is less dire, It's two radii, that's the fire.
Stories
Imagine a pizza slice (sector) and leftovers (segment). Each angle gives a new piece of pizza!
Memory Tools
S.E.C. - Sectors Enclose Chords.
Acronyms
S.C.A.L.E. - Sector Calculation reduces Arc Length Area Equally.
Flash Cards
Glossary
- Sector
A portion of a circle enclosed by two radii and the corresponding arc.
- Segment
The area enclosed between a chord and the arc corresponding to that chord.
- Minor Sector
The smaller sector formed by a given angle at the center.
- Major Sector
The larger sector formed by subtracting the minor sector from the whole circle.
- Area of a Sector
The amount of space inside a sector, calculated using the formula \(\frac{\theta}{360} \times \pi r^2\).
- Arc Length
The distance along the arc of the sector calculated by \(\frac{\theta}{360} \times 2\pi r\).
- Area of Segment
The area of a segment is the area of the sector minus the area of the triangle formed by the radii.
Reference links
Supplementary resources to enhance your learning experience.
