Summary
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Tangents
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, let's discuss tangents to circles. Can anyone define what a tangent is?

Isn't a tangent a line that touches a circle at one point?

Exactly, Student_1! A tangent intersects the circle at just one point. Now, what can you tell me about the relationship between a tangent and the radius at the point of contact?

I think the tangent is perpendicular to the radius!

Great job! That's an important property. We can remember this with the acronym 'TRP' — Tangent is Perpendicular to the Radius.

So, each point on the circle has one tangent?

Correct! One point, one tangent. Let's summarize: a tangent touches the circle at just one point and is perpendicular to the radius at that point.
Lengths of Tangents
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s talk about the lengths of tangents from an external point. What happens when we draw tangents from a point outside the circle?

Are there two tangents from an external point?

That's right! And what's interesting is that both tangents are of equal length. Can anyone tell me why this is the case?

It must be because they meet the circle at the same angle or something?

Good thought! The triangles formed by the radius and tangents are congruent, so the tangents must be equal. Remember the phrase 'Equal Lengths from the Same Point!' which sums up this property.

So if we know one tangent length, we know the other?

Exactly. This property is really helpful in geometry. Let’s summarize again: From an external point, there are two tangents to a circle, and their lengths are equal.
Practical Applications
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s look at practical applications of tangents to circles. Can anyone think of a real-world scenario where tangents are relevant?

Like when two streets meet at a circular park?

Perfect! The roads can be thought of as tangents to the circular park. What do you think happens at the interaction point?

That point is where both roads touch the park?

Exactly! Similarly, engineers use these principles in designing roadways and circular intersections. Let’s conclude by repeating: Tangents have real-life applications in various fields like engineering and design.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we review the concept of a tangent to a circle, noting that it is perpendicular to the radius at the contact point and that the lengths of tangents from an external point to the circle are equal.
Detailed
Detailed Summary
In this chapter, we focused on the concept of tangents related to circles. A tangent is a line that touches a circle at exactly one point, known as the point of contact. Crucially, a tangent to a circle is perpendicular to the radius that extends to the point of contact. This relationship helps in various geometric constructions and proofs. Additionally, when drawing tangents from an external point to the circle, it is important to understand that the lengths of these tangents are equal. This property is useful for solving problems involving circles and tangents.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Meaning of a Tangent to a Circle
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- The meaning of a tangent to a circle.
Detailed Explanation
A tangent to a circle is defined as a straight line that touches the circle at exactly one point. This means that at the point of contact, the tangent does not cross into the circle but instead touches it gently. This is different from a secant, which intersects the circle at two points.
Examples & Analogies
Think of a basketball resting on the ground. If you were to roll a piece of paper to touch the ball without pushing into it, that paper represents the tangent. The point where the paper touches the ball is similar to the point of contact between a tangent and a circle.
Perpendicularity of Tangents and Radii
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- The tangent to a circle is perpendicular to the radius through the point of contact.
Detailed Explanation
When a tangent touches a circle at a point, the radius drawn to the point of contact forms a right angle (90 degrees) with the tangent line. This means that if you were to measure the angle between the radius and the tangent line, it would always be a right angle.
Examples & Analogies
Imagine a wheel rolling on the ground. The radius of the wheel that reaches the ground vertically meets the road at a right angle, just like how a tangent meets a circle at its point of contact.
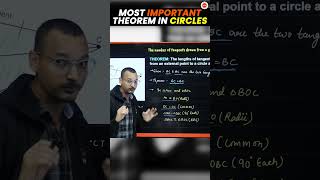
Equality of Tangent Lengths from an External Point
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- The lengths of the two tangents from an external point to a circle are equal.
Detailed Explanation
From any point outside the circle, you can draw two tangents to the circle. The remarkable fact is that these two tangents will always be of equal length. This means if you measure the distance from the external point to each point where the tangents touch the circle, both lengths will be the same.
Examples & Analogies
Consider a flashlight beam hitting a round object like a basketball at two different points. If you stand at a certain distance from the basketball and angle the flashlight toward it, the paths of light from the flashlight to each point where the basketball is touched will be equal in length.
Key Concepts
-
Tangent: A line that touches the circle at one point.
-
Perpendicularity of Tangent and Radius: The tangent is always perpendicular to the radius at the point of contact.
-
Equal Lengths of Tangents: Tangents drawn from an external point to a circle are of equal length.
Examples & Applications
Example: Drawing tangents from a point outside a circle shows that both tangents are of equal length.
Example: Understanding that the tangent at a point is perpendicular to the radius helps in solving geometric problems effectively.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
A line that touches and doesn't stray, a tangent is the way!
Stories
Imagine a circle who has a friend named Tangent that hugs it tight, only touching at one spot while staying out of sight. Together they dance around the center, never crossing but always near.
Memory Tools
TRP – Tangent, Radius, Perpendicular.
Acronyms
TANGENT
'Touching A Normal generally
unless Extending Near Tangentially.'
Flash Cards
Glossary
- Tangent
A line that touches a circle at exactly one point.
- Radius
A line segment from the center of a circle to any point on the circle.
- Point of Contact
The specific point where a tangent intersects a circle.
Reference links
Supplementary resources to enhance your learning experience.
