Solution of a Quadratic Equation by Factorisation
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Roots of Quadratic Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome, class! Today, we will be learning about the roots of quadratic equations. Can anyone remind me what a quadratic equation typically looks like?

Is it ax² + bx + c = 0, where a is not zero?

Exactly! Now, if I plug a number into this equation and it makes the left side equal to zero, what do we call that number?

It's called a root or a solution of the quadratic equation!

Great! So, let's remember, the roots of a quadratic equation are the values that satisfy it. For example, if we consider the equation 2x² - 3x + 1 = 0, and I tell you that x = 1 is a root. What does this mean?

It means that when you replace x with 1, it makes the equation equal to zero.

Correct! That’s crucial for factorization. Let’s recap: roots are the solutions of the equation where the equation equals zero.
Factoring Quadratic Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, who remembers how to factorize a quadratic equation?

We can split the middle term for some quadratics!

Exactly! Let's look at 2x² - 5x + 3 as an example. How would you factor that?

We could express -5x as -2x - 3x. Then it becomes 2x² - 2x - 3x + 3.

Exactly! Now can anyone tell me what we do next after splitting the terms?

We group them and factor each part!

Yes, good job! We group as (2x² - 2x) + (-3x + 3) which factors to give us (2x - 3)(x - 1).

So now we can find our roots by setting each factor to zero. What do we get?

We get x = 1 and x = 1.5 or 3/2!
Application of Quadratic Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we have factored equations, can anyone provide an example of a real-world situation where we might use quadratic equations?

The one about the charity building a prayer hall!

Right! We formed the equation based on area! What was that equation?

It was 2x² + x - 300 = 0, where x was the breadth of the hall.

Perfect. And after we factor that, what do we need to ensure?

We need to make sure that our solutions make sense in the context!

Absolutely! And the roots must be positive since a measurement can't be negative. This ties back to understanding the application of what our equations represent.
Examples of Finding Roots
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's now find the roots of another equation together. Consider 6x² - x - 2 = 0. Student_4, how would you start?

We should first rearrange the equation to factorize it.

Correct! What would you split -x into?

It can be -4x + 3x because -4 * 3 gives us -12.

Nice! What do we do next?

Then we group the terms: 6x² + 4x - 3x - 2.

Excellent! Factor from each group and what do we have?

(3x - 2)(2x + 1)!

Perfect! So now we set both factors to zero and find our solutions. Remember: always verify your roots. Let’s recap today’s lessons on roots and factorization!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, students learn how to find the roots of quadratic equations using factorization, exploring various examples and the mathematical reasoning behind identifying solutions that satisfy the quadratic equation.
Detailed
In Chapter 4.3, students explore the solution of quadratic equations through factorization. A quadratic equation generally takes the form ax² + bx + c = 0, with a non-zero coefficient a. To find roots, students learn that any real number α is a root if substituting it into the equation satisfies it (i.e., it results in zero). The process of factorization is emphasized as a method to break down the quadratic polynomial into simpler linear factors. The section includes illustrative examples, such as finding the roots of the equations 2x² - 5x + 3 = 0 and 6x² - x - 2 = 0, demonstrating the splitting of the middle term and the significance of equating factors to zero to find the solutions. Further emphasis is placed on representing real-world problems as quadratic equations, reinforcing the practical applications of the concepts learned.
Youtube Videos


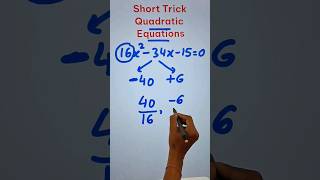







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Roots
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Consider the quadratic equation 2 x² – 3x + 1 = 0. If we replace x by 1 on the LHS of this equation, we get (2 × 1²) – (3 × 1) + 1 = 0 = RHS of the equation. We say that 1 is a root of the quadratic equation 2x² – 3x + 1 = 0. This also means that 1 is a zero of the quadratic polynomial 2 x² – 3x + 1.
Detailed Explanation
In this chunk, we see the concept of roots in a quadratic equation. A root of an equation is a value that makes the equation true. Here, substituting x = 1 into the equation validates that the left-hand side equals the right-hand side (zero). Therefore, 1 is acknowledged as a root. We also establish that finding roots is the same as determining the values where the corresponding quadratic polynomial evaluates to zero.
Examples & Analogies
Imagine you are trying to balance a seesaw. The point where it balances is analogous to the root of an equation; just like a seesaw balances at a specific point, an equation holds true at specific x-values.
Definition of Roots
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In general, a real number α is called a root of the quadratic equation ax² + bx + c = 0, a ≠ 0 if a α² + bα + c = 0. We also say that x = α is a solution of the quadratic equation , or that α satisfies the quadratic equation.
Detailed Explanation
This chunk explains that a number α is identified as a root if substituting it back into the equation results in zero. This illustrates not simply a definition but also indicates the relationship between solutions and roots, emphasizing that roots of quadratics also represent the x-values where the polynomial intersects the x-axis.
Examples & Analogies
Think of it as a treasure map: the solutions to the equation are the coordinates where 'X' marks the spot. Just like finding the treasure at those coordinates makes sense, finding roots provides specific values of x that solve the equation.
Maximum Roots for Quadratics
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Note that the zeroes of the quadratic polynomial ax² + bx + c and the roots of the quadratic equation ax² + bx + c = 0 are the same. You have observed, in Chapter 2, that a quadratic polynomial can have at most two zeroes. So, any quadratic equation can have at most two roots.
Detailed Explanation
Here, we highlight that both the roots and the zeros refer to the same concept in quadratic equations. Since a quadratic polynomial can have a maximum of two distinct zeroes, any corresponding quadratic equation will also yield up to two roots. This establishes a fundamental property of quadratic equations in mathematics.
Examples & Analogies
Imagine a bus route that has two stops before returning to the station. Those stops represent the two roots or zeroes—just as there can only be at most two designated stops on a given route, a quadratic polynomial is limited to two roots.
Factorisation of Quadratic Equations
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
You have learnt in Class IX, how to factorise quadratic polynomials by splitting their middle terms. We shall use this knowledge for finding the roots of a quadratic equation.
Detailed Explanation
In this chunk, we link what students learned in previous classes about factorisation to the current topic. The process of factorisation involves rewriting a quadratic equation as a product of its linear factors. By doing so, it becomes easier to identify the roots of the function. This foundational skill from Class IX is crucial as it allows students to solve quadratic equations effectively.
Examples & Analogies
Imagine you are breaking down a complex puzzle into simpler pieces. Each factor represents a piece of the puzzle. When combined correctly, these pieces resolve the main problem of finding the roots of the equation, much like putting together a puzzle reveals the entire image.
Example of Factorisation Method
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Example 3: Find the roots of the equation 2x² – 5x + 3 = 0, by factorisation. Let us first split the middle term – 5x as -2x – 3x....
Detailed Explanation
This example showcases the factorisation technique. In it, we replace -5x with -2x and -3x, making it easier to combine like terms and factor the quadratic polynomial. By setting the factors equal to zero, we can derive the roots of the equation, clearly demonstrating the utility of factorisation in quadratic equations.
Examples & Analogies
Think of this as dissecting a larger task into smaller, manageable segments. Like cooking a complicated dish by breaking it down into basic steps, factorising makes solving the quadratic simpler.
Solving Further Examples
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Example 4: Find the roots of the quadratic equation 6x² - x - 2 = 0. Solution: We have... (continued)
Detailed Explanation
This chunk provides further examples where the factorisation method is applied. Students will see how different quadratic equations can be factored similarly to find their roots. By following each step methodically, learners can grasp the importance of practice in mastering factorisation.
Examples & Analogies
Just as a mechanic follows a procedure to fix a car engine, students follow procedures in solving quadratic equations. Each step is crucial to achieving the correct outcome, forging a parallel in understanding.
Key Concepts
-
Roots of Quadratic Equations: Values that satisfy the equation.
-
Factorization Method: Splitting the middle term to find roots.
-
Real-world Applications: Quadratic problems represented mathematically.
-
Discriminant: A tool to determine the type of roots.
Examples & Applications
Finding the roots of 2x² - 5x + 3 = 0 by factorization.
Solving 6x² - x - 2 = 0 using the factorization method.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Quadratics are neat, roots we must find, factor them fast, and use your mind!
Stories
Once upon a time, there were two friends called Roots and Factor who went on an adventure to solve equations, unlocking secrets with every factor they found.
Memory Tools
To remember the quadratic formula: 'A-B-C, Over A's two, gives us the roots we pursue!'
Acronyms
R.F.D. - Roots, Factorization, and Discriminant; key concepts in quadratics!
Flash Cards
Glossary
- Quadratic Equation
An equation of the form ax² + bx + c = 0, where a, b, and c are constants, and a is not zero.
- Roots
The values of x that satisfy a quadratic equation, making it equal to zero.
- Factorization
The process of breaking down an expression into simpler products, specifically into linear factors in the case of quadratic equations.
- Zeroes of a Polynomial
The x-values that make the polynomial equal to zero.
- Discriminant
The expression b² - 4ac that determines the nature of the roots of a quadratic equation.
Reference links
Supplementary resources to enhance your learning experience.
