Enrol to start learning
Reading is open to everyone. Enrolling is free, and it is what unlocks the audio lessons, practice tests and progress tracking.
6.2.1. Some interesting patterns
Interactive Audio Lesson
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free account
Today, we will explore how perfect cubes can be expressed as the sum of consecutive odd numbers. Can anyone give me an example of a perfect cube?
Eight! That's 2 cubed.
Correct! Eight can also be expressed as 3 + 5. Let's express some more cubes this way!
So 27 is 7 + 9 + 11, right?
Absolutely! And how about we find the sum of odd numbers needed to reach 10³ now?
I think it's 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19!
That sums up to 1000!
Great job! Summing consecutive odd numbers gives us an excellent insight into cube numbers.
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free account
Now, let’s look at the differences between cubes. For example, what do you think 3³ - 2³ equals?
That is 27 - 8, which equals 19.
Well done! But we can express that as 1 + 2 × 1 × 3! Isn't that fascinating?
So we can see some pattern each time we find the difference?
Exactly! The formula we derive helps visualize these calculations better. Let’s try to calculate more together.
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free accountLastly, let's cover prime factorization. Remember that each prime factor of a cube appears three times. Who can help me confirm these factors?
For example, 8 is 2 × 2 × 2, and that proves it's a cube!
Great job! So if I give you the number 27, how would you break that down?
That's 3 × 3 × 3!
Exactly! Now, let’s check if 64 is a perfect cube using prime factorization.
It is because it's 2 × 2 × 2 × 2 × 2 × 2, which makes it 4 twos or 2³!
Great teamwork, everyone! Prime factorization is a crucial skill.
Overview
Short Summary
This section explores interesting patterns found in the sum of consecutive odd numbers and their relationship to perfect cubes.
Medium Summary
In this section, students learn how consecutive odd numbers can be summed to yield perfect cubes, discover patterns in cube root calculations, and analyze the structure of prime factorizations leading to cube formation. The unique properties of perfect cubes are reinforced through various exercises and examples.
Detailed Summary
Some Interesting Patterns
This section focuses on intriguing patterns related to numbers, particularly regarding the sums of consecutive odd numbers which equate to perfect cubes.
Key Points:
-
Sum of Consecutive Odd Numbers:
- Each perfect cube can be expressed as the sum of an increasing series of consecutive odd numbers. For instance:
- 1 = 1 (1³)
- 3 + 5 = 8 (2³)
- 7 + 9 + 11 = 27 (3³)
- And so forth.
- This pattern prompts exploration into how many consecutive odd numbers sum to other cubes, such as 10³.
- Each perfect cube can be expressed as the sum of an increasing series of consecutive odd numbers. For instance:
-
Patterns in Cube Differences:
- The differences between cubes have unique representations, for instance:
- 2³ - 1³ = 1 + 2 × 1 × 1.
- These differences maintain a consistent structure, suggesting a mathematical relationship valuable for problem-solving and analysis of cubes.
- The differences between cubes have unique representations, for instance:
-
Prime Factorization of Cubes:
- Each prime factor in a number's cube appears three times in its prime factorization, which can be leveraged to determine whether a number is a perfect cube.
- Practical exercises guided by these observations solidify understanding, including establishing whether given numbers are perfect cubes based on their prime factorizations.
Reference YouTube Videos
Audio Book
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free account- Adding consecutive odd numbers
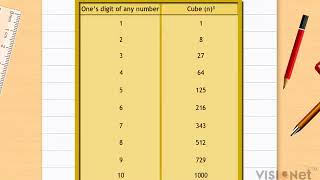
Observe the following pattern of sums of odd numbers.
1 = 1 = 1³
3 + 5 = 8 = 2³
7 + 9 + 11 = 27 = 3³
13 + 15 + 17 + 19 = 64 = 4³
21 + 23 + 25 + 27 + 29 = 125 = 5³
Is it not interesting? How many consecutive odd numbers will be needed to obtain the sum as 10³?
TRY THESE
Express the following numbers as the sum of odd numbers using the above pattern? (a) 63 (b) 83 (c) 73
Detailed Explanation
In this chunk, we explore the relationship between adding consecutive odd numbers and perfect cubes. The cube of a number n (n³) is represented as the sum of the first n consecutive odd numbers. For instance:
- 1 (1³) is obtained from including just the first odd number (1).
- 2³ (8) is the sum of the first two odd numbers (3 + 5).
- Similarly, 3³ (27) arises from adding 7, 9, and 11. This pattern continues until 5³, representing the sum of 21 through 29. The section challenges you to find how many consecutive odd numbers sum up to 10³ (1000), encouraging students to engage with mathematical concepts interactively.
Examples & Analogies
To relate this to a real-life scenario, think of building a structure with blocks. If you add layers of blocks to create a square base, the number of blocks in each layer corresponds to consecutive odd numbers. This method shows how shapes can grow into cubes, similar to how each added layer contributes to completing a larger cube structure.
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountConsider the following pattern.
2³ – 1³ = 1 + 2 × 1 × 3
3³ – 2³ = 1 + 3 × 2 × 3
4³ – 3³ = 1 + 4 × 3 × 3
Using the above pattern, find the value of the following.
(i) 7³ – 6³ (ii) 12³ – 11³ (iii) 20³ – 19³ (iv) 51³ – 50³
Detailed Explanation
This chunk discusses how to find the difference of cubes using a specific pattern. For cubes of succeeding integers, the difference can be expressed in a streamlined equation. For example:
- The difference between 2³ and 1³ is structured as 2³ - 1³ = 1 + 2×1×3 which represents a systematic way to express the result. This pattern shows that the difference of cubes can become more manageable to calculate.
Examples & Analogies
Imagine a stack of boxes. If you take a smaller box away from a larger one, you can visualize the space left in simpler terms. This visualization symbolizes the pattern found within the differences of cubes methodically, making it easier to understand how larger quantities can be broken down.
Key Concepts
Core takeaways and short definitions to help you quickly recall the key ideas from this section.
Perfect Cubes: Numbers formed by multiplying an integer by itself three times.
Sum Patterns: Perfect cubes can be expressed as the sum of consecutive odd numbers.
Prime Factorization: Each prime factor appears three times in a perfect cube.
Examples
Memory Aids
Interactive tools to help you remember key concepts