LINES AND ANGLES
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Lines and Angles
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're diving into lines and angles! Can anyone recall what defines a line in geometry?

A line is straight and extends indefinitely in both directions.

Correct! Now, what about a line segment and a ray?

A line segment has two endpoints, and a ray has one endpoint and extends infinitely in one direction.

Exactly! Let's remember this by thinking of 'ray' like a flashlight beam, starting from a point and shining forward.
Types of Angles
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Angles are formed when two rays meet. Who can name the different types of angles we have?

There are acute, right, obtuse, straight, and reflex angles!

Very good! Let's create a quick mnemonic: 'All Right Owls Sit Relaxed' for Acute, Right, Obtuse, Straight, and Reflex. Can someone explain what an acute angle is?

An acute angle measures less than 90°.

Great! And how about the obtuse angle?

It measures more than 90° but less than 180°.
Adjacent and Complementary Angles
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's delve into adjacent angles. Who can tell me what adjacent angles are?

Adjacent angles share a common vertex and a common arm.

That's right! Remember that adjacent angles can also form linear pairs. What does that mean?

If they form a linear pair, their angles add up to 180°!

Exactly! And how about complementary angles?

They are two angles that sum to 90°.
Intersecting Lines and Angles
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s discuss intersecting lines. When two lines intersect, what can we say about the angles formed?

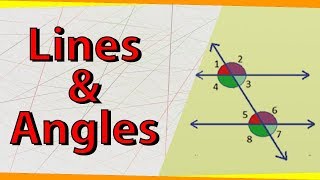
The angles opposite each other are called vertically opposite angles and they are equal.

Correct! Remember the acronym 'V-O-A': Vertically Opposite Angles are always equal. Can anyone give an example?

If two lines intersect to form angles of 40° and 140°, then the opposite angles would also be 40° and 140°.
Parallel Lines and Transversals
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s move to parallel lines. What happens when a transversal crosses two parallel lines?

The corresponding angles are equal!

Exactly! Remember 'C-A-E': Corresponding Angles are Equal. Can someone find an example in our daily life where we see parallel lines?

The lines on a road or railway tracks!

Great observation! This concept is important in various real-life applications, particularly in construction and design.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, students explore the definitions and properties of lines and angles, including concepts of intersecting lines, adjacent angles, vertically opposite angles, and the significance of parallel lines. The section emphasizes the practical applications of these concepts in various fields.
Detailed
Detailed Summary
In this section, we delve into the fundamental concepts of lines and angles, building on prior knowledge of geometric principles. A line, defined as a straight path extending indefinitely, can be represented as a line segment or ray, depending on whether it has two endpoints or one. The formation of angles, created by two rays sharing a common endpoint (the vertex), is explored in detail, categorizing them into types such as acute, right, obtuse, straight, and reflex angles.
Key concepts include:
- Complementary and Supplementary Angles: Angles that sum to 90° and 180°, respectively.
- Adjacent Angles: Two angles that share a common vertex and arm but do not overlap.
- Linear Pairs: Two adjacent angles whose non-common arms form a straight line, totaling 180°.
- Vertically Opposite Angles: Angles opposite each other when two lines intersect, which are always equal.
Additionally, the chapter discusses lines in relation to one another, distinguishing between intersecting lines and non-intersecting (parallel) lines, along with axioms governing their relationships. The section concludes with a reminder of the importance of these concepts in practical scenarios like architecture and physics, providing a foundation for more advanced geometric studies.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Lines and Angles
Chapter 1 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In Chapter 5, you have studied that a minimum of two points are required to draw a line...
Detailed Explanation
This introductory paragraph sets the stage for understanding lines and angles. It emphasizes that angles are formed when two lines intersect, and this concept is essential for various practical applications such as architecture and science. It indicates that knowledge of angles allows us to make precise models and drawings, which are crucial in real-life situations.
Examples & Analogies
Consider an architect designing a house. They need to understand how lines and angles work to create a strong and aesthetically pleasing structure. Just like arranging furniture in a room involves ensuring everything fits well at the right angles, building designs must consider angles for doors, windows, and roof lines.
Basic Terms and Definitions
Chapter 2 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Recall that a part (or portion) of a line with two end points is called a line-segment...
Detailed Explanation
This section introduces essential definitions related to lines and angles. A line-segment has two endpoints, while a ray has one endpoint and extends indefinitely in one direction. It also explains collinear points (points on the same line) and various types of angles, such as acute, right, obtuse, straight, and reflex angles.
Examples & Analogies
Imagine a road that represents a line. If you place two landmarks at different points on the road, the distance between them is like a line-segment. If you start at one landmark and point along the road, that’s similar to a ray. Measuring the angle at a street corner helps us categorize whether it’s a sharp turn (acute), a perfect turn (right), or a gentle one (obtuse!).
Properties of Angles
Chapter 3 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
An acute angle measures between 0° and 90°, whereas a right angle is exactly equal to 90°...
Detailed Explanation
This section outlines the types of angles based on their measurements. It explains each type, including acute, right, obtuse, straight, and reflex angles, helping students understand the distinctions between them based on degrees.
Examples & Analogies
Think of the hands of a clock. When the minute hand is at the 12 and the hour hand is at the 1, they form an acute angle. When the minute hand is at the 12 and the hour hand is at the 3, that’s a right angle. If the hour hand is at the 6, that’s a straight angle, and if it goes past 6, it’s obtuse. The representation of angles with the clock makes it relatable and easier to visualize.
Adjacent and Linear Pair of Angles
Chapter 4 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
You have also studied about adjacent angles in the earlier classes...
Detailed Explanation
Adjacent angles share a common vertex and side, but do not overlap. When two adjacent angles add up to form a straight angle (180°), they form what is known as a linear pair. The law of angles among adjacent pairs is crucial for calculating angles in geometrical figures.
Examples & Analogies
Imagine two people standing at a corner of a street, talking (the angles formed by their positioning). Their individual angles of view create adjacent angles, and if they both turn to face away from each other, they create a linear pair as they face opposite directions on the same line.
Vertically Opposite Angles
Chapter 5 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
You may also recall the vertically opposite angles formed when two lines intersect each other...
Detailed Explanation
When two lines intersect, they create pairs of angles opposite each other that are called vertically opposite angles. This section highlights that these angles are equal, which is a fundamental principle in geometry.
Examples & Analogies
Consider a crossroad with two streets crossing each other. The angles formed at each intersection hold their opposite counterparts. If you look at the angles formed between the streets when they meet, the angles facing each other directly are equal—like two friends standing opposite each other mirroring each other's stance.
Intersecting and Non-intersecting Lines
Chapter 6 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Recall the notion of a line, that it extends indefinitely in both directions...
Detailed Explanation
This chunk explains the difference between intersecting lines (which meet at one point) and non-intersecting (parallel) lines that never meet. The concept of distance between parallel lines is also introduced.
Examples & Analogies
Think of train tracks as parallel lines. They are always a fixed distance apart and never meet. On the other hand, roads that cross each other create intersections, where you must yield to traffic from different directions.
Pairs of Angles and Their Relationships
Chapter 7 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In Section 6.2, you have learnt the definitions of some of the pairs of angles such as complementary angles...
Detailed Explanation
This section revisits the relationships among different pairs of angles, like complementary (two angles that add up to 90°) and supplementary angles (which add up to 180°). It highlights how these relationships form the basis for solving angle problems in geometry.
Examples & Analogies
Imagine a right triangle where one angle is 30°. The angle next to it must be 60° so they complement each other. In a presentation, two slides that together make up a complete story—one slide summarizes the problem (30°) and the next offers the solution (60°), combining to make a compelling narrative.
Using Axioms and Theorems
Chapter 8 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Axiom 6.1: If a ray stands on a line, then the sum of two adjacent angles so formed is 180°...
Detailed Explanation
Axioms and theorems are foundational rules used in geometry to ascertain relationships between angles and lines. Axiom 6.1 states that when a ray stands on a line, the adjacent angles formed will always sum up to 180°, while the converse of this statement is also valid.
Examples & Analogies
Think of a straight road with a road sign indicating the direction of a turn. The angle formed between where the road continues straight (180°) and the turn represents adjacent angles like those described in the axiom. Just like the roads signal the direction, axioms provide essential guidance to reach geometric conclusions logically.
Lines Parallel to the Same Line
Chapter 9 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If two lines are parallel to the same line, will they be parallel to each other?...
Detailed Explanation
The section explains that if two lines are parallel to the same line, they are also parallel to each other. This is established through the concept of corresponding angles formed by a transversal intersecting these lines.
Examples & Analogies
Consider two highways, one running north and another running south, both parallel to a river flowing east. If a road crosses the river (like our transversal), the angles formed with the highways remain consistent, ensuring that the two highways, like parallel lines, will never meet.
Summary of Key Points
Chapter 10 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In this chapter, you have studied the following points:...
Detailed Explanation
This concluding section summarizes the main takeaways from the chapter. It reinforces the importance of understanding angles and lines, along with their interrelationships and practical applications.
Examples & Analogies
Just like how a recipe summarizes all the ingredients needed for a dish, this summary encapsulates the vital points to remember about lines and angles before moving on to more complex geometric concepts.
Key Concepts
-
Line: A straight path that extends indefinitely in both directions.
-
Angle: Formed by two rays sharing a common endpoint.
-
Acute Angle: Less than 90°.
-
Obtuse Angle: More than 90° and less than 180°.
-
Complementary Angles: Two angles summing to 90°.
-
Linear Pair: Adjacent angles that sum to 180°.
Examples & Applications
Example 1: If angle A = 30°, then its complementary angle B = 90° - 30° = 60°.
Example 2: When two lines intersect at point O and form angles of 45° and 135°, the vertically opposite angles are equal.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Angles that meet at a point, adjacent angles in a joint.
Stories
Imagine two roads crossing; the angles opposite are always bossing each other with their equal measures.
Memory Tools
Remember 'C-A-E' for Corresponding Angles are Equal when lines are parallel.
Acronyms
Use 'A-O-S' for Acute, Obtuse, and Straight angles to remember their classifications.
Flash Cards
Glossary
- Angle
A figure formed by two rays sharing a common endpoint called the vertex.
- Acute Angle
An angle that measures less than 90°.
- Obtuse Angle
An angle that measures more than 90° but less than 180°.
- Adjacent Angles
Two angles that share a common vertex and a common arm.
- Complementary Angles
Two angles whose sum is 90°.
- Supplementary Angles
Two angles whose sum is 180°.
- Linear Pair
A pair of adjacent angles whose non-common arms form a straight line.
- Vertically Opposite Angles
Angles that are opposite each other when two lines intersect, which are always equal.
- Parallel Lines
Lines in a plane that never meet and are always the same distance apart.
Reference links
Supplementary resources to enhance your learning experience.
