7.3. Criteria for Congruence of Triangles

In earlier classes, you have learnt four criteria for congruence of triangles. Let us recall them.

Draw two triangles with one side 3 cm. Are these triangles congruent? Observe that they are not congruent (see Fig. 7.5).

This introduction sets the stage for understanding what it means for triangles to be congruent. Congruence implies that two triangles have the same shape and size, with corresponding sides and angles that are equal. The given example of drawing two triangles with one side each of 3 cm emphasizes that having just one side equal is not enough for the triangles to be congruent, as additional sides and angles must also be considered.

Think of two identical shoes; if one shoe is missing a key detail, such as the correct size or built, even if they feel similar at first glance, they will not fit right. Similarly, for triangles, it's not enough to have one measurement match; all relevant features must align.

Now, draw two triangles with one side 4 cm and one angle 50° (see Fig. 7.6). Are they congruent? See that these two triangles are not congruent. Repeat this activity with some more pairs of triangles.

Here, we observe another scenario where only one side and one angle are equal. The emphasis is on testing the congruence by drawing and comparing various pairs of triangles. The conclusion drawn from these activities reinforces that knowing just a side and an angle does not guarantee congruence, as the overall configuration of the triangles could differ.

Imagine building a model airplane using different parts. Even if you use one identical wing and a similar engine, the alignment of all components must be precise for the airplane to fly correctly. Just like that, triangles must maintain alignment across all sides and angles to be congruent.

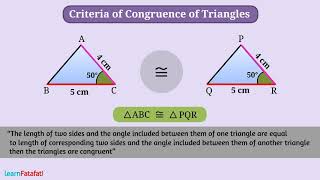
In Fig 7.7, BC = QR, ∠ B = ∠ Q and also, AB = PQ. Now, what can you say about congruence of ∆ABC and ∆PQR? Recall from your earlier classes that, in this case, the two triangles are congruent. This is the first criterion for congruence of triangles.

Axiom 7.1 (SAS congruence rule): Two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle.

This segment presents the SAS (Side-Angle-Side) congruence rule. Here, we see how having two sides and the angle between them equal for two triangles ensures their overall congruence. This criterion is a foundational tool in geometry. Students are encouraged to verify this in practice through constructions of triangles based on these conditions.

Consider two bridges made with the same materials where the main beams are identical in length and the angle of the support is also the same. These structures will behave in the same manner under load due to their congruence, just as congruent triangles will have the same properties.

Let us now take some examples. Example 1: In Fig. 7.8, OA = OB and OD = OC. Show that (i) ∆ AOD ≅ ∆ BOC and (ii) AD || BC.

This example illustrates the practical application of the SAS rule. The equality of two sides and the included angle (formed by the line segments and transversals) leads to the conclusion that these two triangles are congruent, and hence the lines AD and BC are parallel. This showcases how geometric properties can derive from congruence.

Think of constructing a skateboard ramp; if two sections are built with the same measurements for safety (length and angle), they ensure that skaters can use both parts seamlessly without risk, just like the parallel configuration derived from the triangles being congruent.

Next, we learn about additional criteria. For instance, if two angles and one included side are equal, we have the ASA (Angle-Side-Angle) criterion. This can also be proved through constructing examples and observing congruence between triangles drawn with those conditions.

The ASA criterion gives us another method to determine triangle congruence. By ensuring that two angles and the side between them are equal, we can conclude that the triangles must indeed be the same shape and size. This section promotes geometric dexterity by requiring students to visualize and construct triangles that fit the ASA model.

Imagine two sailboats that are rigged identically with matching sails and a sail length. Because of these matching characteristics, they'll handle the same way in the wind. This is akin to how triangles behave under the criteria of ASA; their internal angles dictate their overall configuration and congruence.

Finally, it is established that equality of three angles is not sufficient for congruence, reinforcing the need for incorporating at least one side equality into triangle properties.

In closing, this section underlines a vital point about triangle congruence: having three angles equal does not guarantee congruence if the sides differ. Thus, students conclude with a robust understanding of how congruence functions across various criteria, and need to incorporate conditions judiciously.

Consider two triangles you might sketch; although they could share angle shapes (like drawn protractors), if one triangle's base is longer than another, they won't be the same triangle. This practical visual can help students grasp why at least one side parameter is essential.

--