Enrol to start learning
Reading is open to everyone. Enrolling is free, and it is what unlocks the audio lessons, practice tests and progress tracking.
9.2.1. TO CALCULATE THE VALUE OF GRAVITY
Interactive Audio Lesson
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free account
Today, we'll learn about gravitational acceleration, or 'g'. Does anyone know what 'g' represents?
Isn't it the acceleration that objects experience when they fall?
Exactly! It's the acceleration due to gravity near the Earth's surface. It averages about 9.8 m/s². Remember that 'g' is crucial in understanding how objects move under gravity. Can anyone think of a situation where we use 'g'?
When we drop something from a height, right?
Exactly! When you drop a ball, gravity pulls it down, accelerating it at 'g'. Let's remember 'g' as 'Going down fast!' for quick recall.
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free account
Now, let’s calculate 'g'. We use the formula: g = GM/R². What do G, M, and R stand for?
G is the gravitational constant, M is the mass of the Earth, and R is the radius of the Earth!
Correct! G is about 6.67 × 10^-11 N m²/kg², M is 6 × 10²⁴ kg, and R is 6.4 × 10^6 m. Could anyone plug these values into the formula?
Sure! So, g = (6.67 × 10^-11 N m²/kg² * 6 × 10²⁴ kg) / (6.4 × 10^6 m)².
Great job! What do we get after calculating that?
We get approximately 9.8 m/s²!
Perfect! Now, how does 'g' change at different locations, like the poles versus the equator?
It's stronger at the poles due to the Earth's shape and rotation, right?
Absolutely! Let's remember this with the acronym 'PEAR': Poles have a higher 'g'.
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free accountNow, let’s talk about the applications of 'g'. Can anyone provide an example of its use in engineering or science?
In calculating the weight of objects or during free fall experiments.
Correct! In free fall, every object accelerates towards Earth at 'g', assuming no air resistance. There's a saying: 'What goes up must come down at 'g'!' Why is it important in launching rockets?
We need to calculate how fast they need to go to escape Earth's gravitational pull.
Exactly! That's called escape velocity, which directly relates to 'g'. Let's summarize: 'g' not only explains falling objects but also is crucial in various scientific fields.
Overview
Short Summary
This section discusses how to calculate the acceleration due to gravity, denoted as 'g', using the universal gravitational constant and other values.
Medium Summary
In this section, we learn the formula for calculating the acceleration due to gravity 'g' by substituting known values like the universal gravitational constant (G), the mass of the Earth (M), and the radius of the Earth (R). It also explains the importance of understanding how 'g' varies in different locations.
Detailed Summary
Detailed Summary
In this section, we delve into the calculation of gravitational acceleration, commonly referred to as g. Gravitational acceleration is a crucial concept in physics as it describes the rate at which objects accelerate towards the Earth due to gravitational attraction. The value of g is typically approximated as 9.8 m/s² near the Earth's surface, but it can vary based on geographical location (greater at the poles than the equator) and altitude.
To compute g, we utilize the equation derived from Newton's Law of Gravitation:
Where:
- G is the universal gravitational constant (approximately
6.67 × 10^-11 N m²/kg²), - M is the mass of the Earth (
6 × 10^24 kg), and - R is the radius of the Earth (
6.4 × 10^6 m).
By substituting these values into the equation, we arrive at the calculated value of g, which is approximately 9.8 m/s². This section emphasizes the universality of gravitational acceleration and its relevance to the motion of objects near the Earth's surface.
Reference YouTube Videos
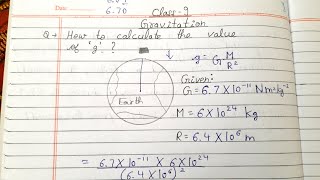
Audio Book
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountTo calculate the value of g, we should put the values of G, M and R in Eq. (9.9), namely, universal gravitational constant, G = 6.7 × 10–11 N m2 kg-2, mass of the earth, M = 6 × 1024 kg, and radius of the earth, R = 6.4 × 106 m.
Detailed Explanation
To find the value of 'g', we use the formula that relates gravitational force to mass and distance. Here, G is the universal gravitational constant, which describes how strong the gravitational force is. M is the mass of the Earth, which determines how much gravitational pull it has, and R is the radius of the Earth, which helps calculate the distance from the Earth's center to its surface. The formula combines these values to compute the acceleration due to gravity at the Earth's surface.
Examples & Analogies
Imagine that gravity is like a giant magnet that pulls objects towards Earth. The strength of this magnet depends on how heavy the magnet is (which represents the Earth's mass, M) and how far away you are from it (which represents the radius, R). So, by plugging these numbers into the gravity formula, we can find out exactly how strong the pull of this 'magnet' is at the surface of the Earth.
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountg = G M / R2 = 6.7×10-11 N m2 kg-2 × 6×1024 kg / (6.4×106 m)2 = 9.8 m s–2.
Detailed Explanation
After substituting the values into the equation, we calculate g by multiplying the gravitational constant (G) by the mass of the Earth (M) and dividing by the square of the radius of the Earth (R²). This calculation simplifies to show that the acceleration due to gravity (g) is approximately 9.8 m/s², which means that any object falling freely towards the Earth accelerates at this rate.
Examples & Analogies
Think of throwing a ball straight up into the air. Every second it goes up, gravity pulls it down by about 9.8 meters per second faster. So if you throw it upwards, it might take a few seconds to reach the top of its arc before coming back down, but the entire time, gravity is working to bring it back to Earth, accelerating the ball downward at that rate.
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountThus, the value of acceleration due to gravity g = 9.8 m s–2.
Detailed Explanation
The value we find for g, which is 9.8 m/s², indicates how much an object's velocity increases every second due to the force of gravity. This unit tells us the change in speed in meters per second for each second of falling time. It is essential for calculating the motion of falling objects on Earth.
Examples & Analogies
Consider a skydiver jumping out of a plane. As they fall, they go faster and faster. The 9.8 m/s² means that every second, they gain about 9.8 meters per second more speed. So, after one second, they're going 9.8 m/s, after two seconds, about 19.6 m/s, and so on, until they reach their terminal velocity where they stop accelerating due to air resistance.
--
Key Concepts
Core takeaways and short definitions to help you quickly recall the key ideas from this section.
Gravitational acceleration ('g') averages 9.8 m/s² near Earth's surface.
The formula for calculating 'g' is g = GM/R², where G is the gravitational constant.
The value of 'g' varies with altitude and location on Earth.
Examples
Memory Aids
Interactive tools to help you remember key concepts
Stories
Flash Cards
Glossary
Gravitational Constant (G)
The universal constant that measures the strength of the gravitational force, approximately 6.67 × 10^-11 N m²/kg².
Acceleration due to Gravity (g)
The acceleration experienced by an object in free fall due to the Earth's gravitational pull, approximately 9.8 m/s².
Mass (M)
The quantity of matter in an object, measured in kilograms (kg).
Radius of Earth (R)
The average distance from the center of the Earth to its surface, approximately 6.4 × 10^6 m.