2.2 - Geometrical Meaning of the Zeroes of a Polynomial
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Linear Polynomials
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's start with linear polynomials, such as y = ax + b. Can anyone tell me what happens to the graph of this polynomial?

The graph is a straight line!

Exactly! And where does it intersect the x-axis?

At the zero of the polynomial!

Right! The zero, or x-intercept, can be found using the formula -b/a. This is the x-coordinate where y equals zero. Can anyone find the zero for y = 2x + 3?

Sure! Setting it to zero gives us 2x + 3 = 0, which means x = -3/2!

Great job! Remember, zeroes are crucial as they show where the polynomial's value turns from positive to negative or vice versa. Let's summarize what we learned.

In summary, linear polynomials intersect the x-axis at exactly one point, which we can calculate using -b/a.
Exploring Quadratic Polynomials
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's discuss quadratic polynomials. Who can define what a quadratic polynomial looks like and its graph?

A quadratic polynomial is in the form y = ax² + bx + c, and its graph is a parabola!

Correct! Can anyone tell me how we find the zeroes on this graph?

By finding the points where the graph intersects the x-axis.

Exactly! There are three possible scenarios: it can intersect at two distinct points, one point (double root), or not intersect at all. Let's take an example with y = x² - 3x - 4. What are the zeroes here?

They are -1 and 4!

That's right! Those zeroes can be found either by factoring or using the quadratic formula. Let's wrap this session up.

In conclusion, quadratic polynomials can have two, one, or no real zeroes based on the shape of their graph.
Zeroes of Cubic Polynomials
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Lastly, let’s talk about cubic polynomials. Who knows what a cubic polynomial looks like?

It has the form y = ax³ + bx² + cx + d.

Great! Now, how many zeroes can cubic polynomials have?

They can have up to three zeroes!

Exactly! Let's look at a cubic polynomial, y = x³ - 4x. What are its zeroes?

The zeroes are -2, 0, and 2!

Right again! Each of these points represents an intersection with the x-axis. Cubic polynomials can change direction twice, hence allowing three distinct intersections. Let’s summarize.

In summary, cubic polynomials can have up to three real zeroes, and understanding their graph shapes helps identify these zeroes.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section explains the significance of zeroes in polynomials through their geometrical representation. It covers how the graphs of linear and quadratic polynomials intersect the x-axis and describes the cases where zeroes can be found in those graphs.
Detailed
Geometrical Meaning of the Zeroes of a Polynomial
The zeroes of a polynomial are the x-values where the polynomial intersects the x-axis, represented as real numbers k such that p(k) = 0. The section examines the importance of these zeroes through their geometrical interpretations in linear and quadratic polynomial graphs.
Key Insights:
- Linear Polynomials: For a linear polynomial p(x) = ax + b (where a ≠ 0), the graph is a straight line that always intersects the x-axis at one point. This intersection represents the zero of the polynomial. The x-coordinate of this intersection can be calculated as -b/a.
- Quadratic Polynomials: The graph of a quadratic polynomial y = ax² + bx + c is a parabola. Depending on the discriminant, it can intersect the x-axis in:
- Two Distinct Points: Two distinct zeroes (two x-values where the graph touches the x-axis).
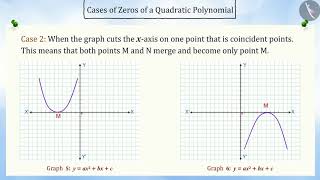
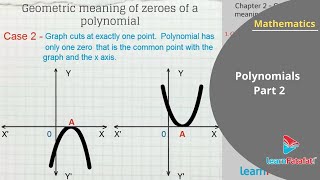
- One Point: Coinciding at one point (one double root).
- No Points: The parabola remains above or below the x-axis, indicating no real zeroes.
The number of zeroes corresponds to the degree of the polynomial, with quadratics having at most two and cubics having at most three. This relationship between the degree of the polynomial and its zeroes is a foundational concept in understanding polynomial behavior.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Zeroes of Polynomials
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
You know that a real number k is a zero of the polynomial p(x) if p(k) = 0. But why are the zeroes of a polynomial so important? To answer this, first we will see the geometrical representations of linear and quadratic polynomials and the geometrical meaning of their zeroes.
Detailed Explanation
A polynomial p(x) has zeroes that indicate specific points where the polynomial touches or crosses the x-axis on a graph. For example, if we have a polynomial p(x) and we find a real number k where p(k)=0, it means that the graph of p(x) intersects the x-axis at that point k. This intersection is crucial for understanding the behavior of the polynomial.
Examples & Analogies
Consider standing on a bridge. The point where the bridge touches the water's surface can be seen as a zero of the bridge's height above water. It represents the point where the bridge is level with the water, similar to how the zero of a polynomial indicates where the polynomial value is zero.
Linear Polynomials and Their Graphical Representation
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Consider first a linear polynomial ax + b, a ≠ 0. You have studied in Class IX that the graph of y = ax + b is a straight line. For example, the graph of y = 2x + 3 is a straight line passing through the points (–2, –1) and (2, 7). From Fig. 2.1, you can see that the graph of y = 2x + 3 intersects the x-axis mid-way between x = –1 and x = –2, that is, at the point (–3/2, 0).
Detailed Explanation
A linear polynomial, which is of the form ax + b, represents a straight line. The point at which this line crosses the x-axis is called its zero. This point can be calculated as x = -b/a. For instance, in the example y = 2x + 3, the zero is found by setting y to 0 and solving for x, which shows where the line intersects the x-axis.
Examples & Analogies
Think of a balance beam. The point where the beam is perfectly horizontal can be compared to the zero of a linear polynomial. Just as the level point is where the weights balance out, the zero of the polynomial is where its value equals zero.
Understanding Quadratic Polynomials
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now, let us look for the geometrical meaning of a zero of a quadratic polynomial. Consider the quadratic polynomial x² – 3x – 4. Let us see what the graph of y = x² – 3x – 4 looks like. If we locate the points listed above on a graph paper, the graph will look like a parabola. The zeroes of the polynomial correspond to the x-coordinates where the graph intersects the x-axis.
Detailed Explanation
Quadratic polynomials have a parabolic graph. The x-coordinates where this curve crosses the x-axis represent the zeroes of the polynomial. For example, when we found the zeroes of the polynomial x² - 3x - 4 to be -1 and 4, these points are where the curve meets the x-axis, showing us the solutions to the equation.
Examples & Analogies
Imagine throwing a ball. The points where the ball touches the ground represent its zero height. Just like the ball travels up and down, the quadratic polynomial parabolically curves up and down with its zeroes signaling when it 'hits' the x-axis.
Cases for Quadratic Polynomial Zeroes
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
From our observation earlier about the shape of the graph of y = ax² + bx + c, the following three cases can happen: Case (i) : Here, the graph cuts the x-axis at two distinct points. Case (ii) : Here, the graph cuts the x-axis at exactly one point. Case (iii) : Here, the graph is either completely above the x-axis or completely below the x-axis.
Detailed Explanation
A quadratic polynomial can have different numbers of zeroes based on the shape of its graph: two distinct zeroes when it intersects at two points, one zero when it just touches the axis at one point, or no zeroes when it stays entirely above or below the x-axis. This shows how the zeroes relate directly to the graph's behavior.
Examples & Analogies
Consider a car going over hills. If the car (graph) just touches the road (x-axis) at the peak of a hill without going down, that represents one zero. If it goes across a flat part and intersects the road, it represents two zeroes. If the car never goes below a certain height (y-value), it shows no zeroes.
Cubic Polynomials and Their Zeroes
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now, what do you expect the geometrical meaning of the zeroes of a cubic polynomial to be? Let us find out. Consider the cubic polynomial x³ – 4x. To see what the graph looks like, we determine a few values and plot them. We find that the graph of y = x³ – 4x intersects the x-axis at three points, -2, 0, and 2.
Detailed Explanation
Cubic polynomials, which have up to three zeroes, can illustrate more complex behavior in their graphs. The points where these graphs intersect the x-axis indicate the zeroes of the polynomial, which can be calculated by setting the polynomial to zero and solving for x.
Examples & Analogies
Picture a roller coaster. The points where the coaster dips below ground level would be the zeroes of a cubic polynomial. As it moves up and down, each crossing above or below the ground level gives a zero, illustrating the polynomial's solutions.
Generalization of Zeroes in Polynomials
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In general, given a polynomial p(x) of degree n, the graph of y = p(x) intersects the x-axis at at most n points. Therefore, a polynomial p(x) of degree n has at most n zeroes.
Detailed Explanation
This principle holds for all polynomials: the highest degree indicates the maximum number of zeroes. For instance, a polynomial of degree 2 (a quadratic) can have up to 2 zeroes, while a cubic polynomial can have up to 3 zeroes. Understanding this concept helps predict the behavior of polynomial graphs.
Examples & Analogies
Think of a soap bubble. The number of times the bubble can hit the ground while rolling down the hill indicates its degree, just like how the maximum number of zeroes correlates to the polynomial's degree.
Key Concepts
-
Zero of a Polynomial: Refers to the values of x where the polynomial intersects the x-axis.
-
Linear Polynomials: Have one zero, represented by the formula -b/a.
-
Quadratic Polynomials: Can have up to two zeroes based on their graph shape (two, one, or none).
-
Cubic Polynomials: Can have up to three zeroes, depending on how many times they intersect the x-axis.
Examples & Applications
Example 1: For the polynomial y = 2x + 3, the zero is x = -3/2.
Example 2: The quadratic polynomial y = x² - 3x - 4 has zeroes at x = -1 and x = 4.
Example 3: The cubic polynomial y = x³ - 4x has zeroes at x = -2, x = 0, and x = 2.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
A quadratic so fair, intersects with care; with shapes to show, two, one, or none, let's go!
Stories
Imagine a racecar (the polynomial) trying to reach two checkpoints (zeroes) at a mountain slope (the graph). Sometimes, it reaches both, sometimes only one, or maybe none at all!
Memory Tools
P.O.S. for Polynomial Observations: Points Of intersection are the zeroes!
Acronyms
Z = Zero, L = Linear, Q = Quadratic, C = Cubic helps identify types and zeroes!
Flash Cards
Glossary
- Polynomial
An algebraic expression formed by the sum of powers in one or more variables multiplied by coefficients.
- Zero of a Polynomial
A real number k such that p(k) = 0, indicating where the polynomial intersects the x-axis.
- Linear Polynomial
A polynomial of degree one, which is represented as y = ax + b.
- Quadratic Polynomial
A polynomial of degree two, expressed as y = ax² + bx + c.
- Cubic Polynomial
A polynomial of degree three, represented as y = ax³ + bx² + cx + d.
- Graph
A visual representation of the relationship between two variables, often plotted in a coordinate system.
- Xaxis
The horizontal axis in a coordinate plane where y=0.
- Intersection
The points where the graph of a function crosses the x-axis.
- Parabola
The U-shaped graph of a quadratic function.
Reference links
Supplementary resources to enhance your learning experience.
