Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mode
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Good morning, students! Today, we're going to start discussing the mode, which is one of the measures of central tendency. Can anyone remind me what we understand by mode?
Isnβt it the value that appears most often in a dataset?
Exactly, Student_1! The mode tells us the most frequent observation. Great job! Now, how do you think we would find the mode in grouped data?
I think we can look at the frequency and find which class has the highest frequency.
Right again! In grouped data, we identify the modal class first, which is the one with the highest frequency. Let's remember this: "Modal Class = Maximum Frequency."
What if we have more than one class that has the same maximum frequency?
Thatβs a good question, Student_3! In such a case, the data would be considered multimodal. However, in our discussions, we'll focus on finding a single mode.
Whatβs the formula we use for finding the mode?
"Great question, Student_4! We use the formula:
Identification of the Modal Class
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
"Letβs have a look at an example frequency distribution for family sizes:
Application of the Mode Formula
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
"Now letβs apply our formula! We have:
Interpreting Mode Results
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's discuss the significance of the mode we calculated. Why do you think knowing the mode is important in real life?
It helps us understand what most people in a group are experiencing, right?
Exactly, Student_3! For example, if we're looking at a dataset of family sizes in a neighborhood, the mode can tell us the most common family size. This can be essential for city planning, providing resources, or even marketing!
So, if we know the mode, we might decide where to put more schools or parks based on family size!
Yes! Understanding the mode helps us make informed decisions based on social trends. Let's remember: 'The mode tells us what is popular or common!'
Recap and Practice
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Alright, class! To recap what we learned today, can someone explain how we go about finding the mode of grouped data?
First, we identify the modal class, then we use the formula with the lower limit and surrounding frequencies.
And if thereβs more than one class with the highest frequency, we just consider one mode, for now.
Exactly, Student_2! Now, let's practice! I will give you some data to find the mode. Remember to identify the modal class first!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section provides an overview of the mode as a measure of central tendency, how to determine the modal class in grouped data, and details the formula used to compute the mode. It also includes several examples to clarify the process.
Detailed
In-Depth Overview of Finding the Mode
This section delves into the concept of mode within the context of grouped data. Recall that the mode is defined as the value that appears most frequently in a dataset. For grouped data, which is often presented in class intervals, the mode can be pinpointed through the identification of the modal class β the class interval that contains the highest frequency. Even when multiple values share the maximum frequency, this section focuses on calculating a single mode.
The mode for grouped data can be computed using the formula:
Mode = l + (f1 - f0) * h / (2f1 - f0 - f2)
Where:
- l = lower limit of the modal class
- h = size of the class interval
- f1 = frequency of the modal class
- f0 = frequency of the class preceding the modal class
- f2 = frequency of the class succeeding the modal class.
The section not only outlines the formula but also presents step-by-step practical examples that illustrate how to apply this formula effectively. For instance, it shows how to identify the modal class from a frequency distribution table and subsequently calculate the mode using the provided formula, enhancing the student's ability to grasp and engage with the material comprehensively.
Youtube Videos
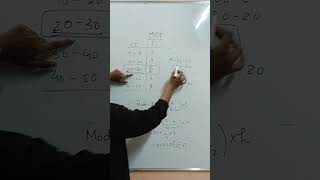
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Mode
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Recall from Class IX, a mode is that value among the observations which occurs most often, that is, the value of the observation having the maximum frequency.
Detailed Explanation
The mode is defined as the number or value that appears most frequently in a dataset. In a simple way, if you list out all the values in the data, you can find the mode by spotting the value that shows up the most.
Examples & Analogies
Imagine you and your friends are counting how many times each type of fruit is chosen during snack time. If apples are picked 6 times while bananas are only picked 3 times, apples are the mode of your fruit selection because they are the most popular choice.
Determining the Mode in Grouped Data
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In a grouped frequency distribution, it is not possible to determine the mode by looking at the frequencies. Here, we can only locate a class with the maximum frequency, called the modal class.
Detailed Explanation
When dealing with grouped data, we cannot directly identify the mode from the frequency counts of individual values. Instead, we identify the 'modal class,' which is the category (or group of values) with the highest frequency. The actual mode is located within this class.
Examples & Analogies
Think of a toy store that has its toys divided into sections based on type: cars, dolls, puzzles, and action figures. If the action figures section has the most toys, the action figures section would be the modal class, but we can't say exactly how many action figures are the most common without looking into individual pieces.
Formula for Calculating the Mode
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The mode is a value inside the modal class, and is given by the formula: Mode = l + (f1 - f0) / (2f1 - f0 - f2) * h where l = lower limit of the modal class, h = size of the class interval (assuming all class sizes to be equal), f1 = frequency of the modal class, f0 = frequency of the class preceding the modal class, f2 = frequency of the class succeeding the modal class.
Detailed Explanation
To find a more precise value for the mode within the modal class, we use a specific formula that incorporates the frequencies of the modal class and its neighboring classes. This formula takes into account how frequently each of these classes occurs and the size of the class intervals to calculate the exact mode value.
Examples & Analogies
Imagine you're trying to pinpoint the most popular toy size in a store. After identifying that 20-inch dolls are the most available size, you might take into account the frequency of 18-inch and 22-inch dolls to determine a precise estimate for the popularity of the 20-inch dolls, just like the formula refines the mode's value based on neighboring frequencies.
Example of Finding the Mode
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us consider the following example to illustrate the use of this formula. Example 5: A survey conducted on 20 households in a locality by a group of students resulted in the following frequency table for the number of family members in a household:
Family size 1 - 3 3 - 5 5 - 7 7 - 9 9 - 11
Number of families 7 8 2 2 1
Find the mode of this data.
Detailed Explanation
In this table, the frequency highest is 8 for the family size class 3-5. Therefore, this class is the modal class. By using the established formula, we can calculate the mode's exact value within this class using its frequencies and limits.
Examples & Analogies
If you were to ask a group of people how many siblings they have and then summarize that into age groups, you would then find the age group with the most replies. For instance, if the age group of 3-5 kids is the highest response, that says something about the families within that age range, just like this table reveals insights about household sizes.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mode: The value that appears most often in a dataset.
-
Modal Class: The class interval with the highest frequency.
-
Frequency: The number of occurrences of a specific value in a dataset.
-
Formula for Mode: Mode = l + (f1 - f0) * h / (2f1 - f0 - f2)
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a survey of family sizes, if the frequencies are: 1-3 = 7, 3-5 = 8, 5-7 = 2, the mode is found in the class 3-5.
-
To calculate the mode using the frequencies 7, 8, 2, 2, and 1 for family sizes, we apply the mode formula once the modal class is identified.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Finding the mode is not a plight, just check the class with the highest height.
π Fascinating Stories
-
Once a class gathered family sizes, they noticed 3-5 sized families were the most popular, just like finding the most liked ice cream flavor on a sunny day!
π§ Other Memory Gems
-
For mode calculation: 'Identify, Clarify, Apply!' - Find the modal class, clarify the values, and then apply the mode formula.
π― Super Acronyms
M.O.D.E - 'Most Often's Data Event' - to keep in mind we are seeking what's most common!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mode
Definition:
The value that occurs most frequently in a dataset.
-
Term: Modal Class
Definition:
The class interval that contains the maximum frequency.
-
Term: Frequency
Definition:
The number of times an observation occurs in a dataset.
-
Term: Cumulative Frequency
Definition:
The total frequency accumulated up to a certain class interval.