Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Concept of 'g'
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we'll learn about gravitational acceleration, or 'g'. Does anyone know what 'g' represents?
Isn't it the acceleration that objects experience when they fall?
Exactly! It's the acceleration due to gravity near the Earth's surface. It averages about 9.8 m/sΒ². Remember that 'g' is crucial in understanding how objects move under gravity. Can anyone think of a situation where we use 'g'?
When we drop something from a height, right?
Exactly! When you drop a ball, gravity pulls it down, accelerating it at 'g'. Let's remember 'g' as 'Going down fast!' for quick recall.
Calculating 'g'
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs calculate 'g'. We use the formula: g = GM/RΒ². What do G, M, and R stand for?
G is the gravitational constant, M is the mass of the Earth, and R is the radius of the Earth!
Correct! G is about 6.67 Γ 10^-11 N mΒ²/kgΒ², M is 6 Γ 10Β²β΄ kg, and R is 6.4 Γ 10^6 m. Could anyone plug these values into the formula?
Sure! So, g = (6.67 Γ 10^-11 N mΒ²/kgΒ² * 6 Γ 10Β²β΄ kg) / (6.4 Γ 10^6 m)Β².
Great job! What do we get after calculating that?
We get approximately 9.8 m/sΒ²!
Perfect! Now, how does 'g' change at different locations, like the poles versus the equator?
It's stronger at the poles due to the Earth's shape and rotation, right?
Absolutely! Let's remember this with the acronym 'PEAR': Poles have a higher 'g'.
Applications of 'g'
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs talk about the applications of 'g'. Can anyone provide an example of its use in engineering or science?
In calculating the weight of objects or during free fall experiments.
Correct! In free fall, every object accelerates towards Earth at 'g', assuming no air resistance. There's a saying: 'What goes up must come down at 'g'!' Why is it important in launching rockets?
We need to calculate how fast they need to go to escape Earth's gravitational pull.
Exactly! That's called escape velocity, which directly relates to 'g'. Let's summarize: 'g' not only explains falling objects but also is crucial in various scientific fields.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we learn the formula for calculating the acceleration due to gravity 'g' by substituting known values like the universal gravitational constant (G), the mass of the Earth (M), and the radius of the Earth (R). It also explains the importance of understanding how 'g' varies in different locations.
Detailed
Detailed Summary
In this section, we delve into the calculation of gravitational acceleration, commonly referred to as g. Gravitational acceleration is a crucial concept in physics as it describes the rate at which objects accelerate towards the Earth due to gravitational attraction. The value of g is typically approximated as 9.8 m/sΒ² near the Earth's surface, but it can vary based on geographical location (greater at the poles than the equator) and altitude.
To compute g, we utilize the equation derived from Newton's Law of Gravitation:
$$ g = \frac{G \times M}{R^2} $$
Where:
- G is the universal gravitational constant (approximately 6.67 Γ 10^-11 N mΒ²/kgΒ²),
- M is the mass of the Earth (6 Γ 10^24 kg), and
- R is the radius of the Earth (6.4 Γ 10^6 m).
By substituting these values into the equation, we arrive at the calculated value of g, which is approximately 9.8 m/sΒ². This section emphasizes the universality of gravitational acceleration and its relevance to the motion of objects near the Earth's surface.
Youtube Videos
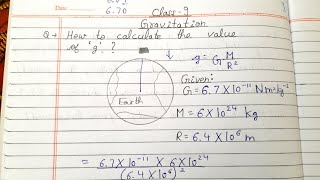
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Calculation of g's Value
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To calculate the value of g, we should put the values of G, M and R in Eq. (9.9), namely, universal gravitational constant, G = 6.7 Γ 10β11 N m2 kg-2, mass of the earth, M = 6 Γ 1024 kg, and radius of the earth, R = 6.4 Γ 106 m.
Detailed Explanation
To find the value of 'g', we use the formula that relates gravitational force to mass and distance. Here, G is the universal gravitational constant, which describes how strong the gravitational force is. M is the mass of the Earth, which determines how much gravitational pull it has, and R is the radius of the Earth, which helps calculate the distance from the Earth's center to its surface. The formula combines these values to compute the acceleration due to gravity at the Earth's surface.
Examples & Analogies
Imagine that gravity is like a giant magnet that pulls objects towards Earth. The strength of this magnet depends on how heavy the magnet is (which represents the Earth's mass, M) and how far away you are from it (which represents the radius, R). So, by plugging these numbers into the gravity formula, we can find out exactly how strong the pull of this 'magnet' is at the surface of the Earth.
Using the Formula for g
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
g = G M / R2 = 6.7Γ10-11 N m2 kg-2 Γ 6Γ1024 kg / (6.4Γ106 m)2 = 9.8 m sβ2.
Detailed Explanation
After substituting the values into the equation, we calculate g by multiplying the gravitational constant (G) by the mass of the Earth (M) and dividing by the square of the radius of the Earth (RΒ²). This calculation simplifies to show that the acceleration due to gravity (g) is approximately 9.8 m/sΒ², which means that any object falling freely towards the Earth accelerates at this rate.
Examples & Analogies
Think of throwing a ball straight up into the air. Every second it goes up, gravity pulls it down by about 9.8 meters per second faster. So if you throw it upwards, it might take a few seconds to reach the top of its arc before coming back down, but the entire time, gravity is working to bring it back to Earth, accelerating the ball downward at that rate.
Understanding the Units
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus, the value of acceleration due to gravity g = 9.8 m sβ2.
Detailed Explanation
The value we find for g, which is 9.8 m/sΒ², indicates how much an object's velocity increases every second due to the force of gravity. This unit tells us the change in speed in meters per second for each second of falling time. It is essential for calculating the motion of falling objects on Earth.
Examples & Analogies
Consider a skydiver jumping out of a plane. As they fall, they go faster and faster. The 9.8 m/sΒ² means that every second, they gain about 9.8 meters per second more speed. So, after one second, they're going 9.8 m/s, after two seconds, about 19.6 m/s, and so on, until they reach their terminal velocity where they stop accelerating due to air resistance.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Gravitational acceleration ('g') averages 9.8 m/sΒ² near Earth's surface.
-
The formula for calculating 'g' is g = GM/RΒ², where G is the gravitational constant.
-
The value of 'g' varies with altitude and location on Earth.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An object in free fall accelerates at approximately 9.8 m/sΒ² until it reaches the ground.
-
Calculating 'g' from values of G, M, and R shows how gravitational force works.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
When objects drop and donβt sway, g brings them down in a steady way.
π Fascinating Stories
-
Once there was a curious student who dropped a ball from a tower. To their surprise, it hit the ground in 9.8 seconds, teaching them about gravitational pull!
π§ Other Memory Gems
-
GMR β Gravitational Mass Radius for remembering the formula for 'g'.
π― Super Acronyms
Remember 'GEM'
- Gravitational constant
- Earthβs mass
- radius to calculate 'g'.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Gravitational Constant (G)
Definition:
The universal constant that measures the strength of the gravitational force, approximately 6.67 Γ 10^-11 N mΒ²/kgΒ².
-
Term: Acceleration due to Gravity (g)
Definition:
The acceleration experienced by an object in free fall due to the Earth's gravitational pull, approximately 9.8 m/sΒ².
-
Term: Mass (M)
Definition:
The quantity of matter in an object, measured in kilograms (kg).
-
Term: Radius of Earth (R)
Definition:
The average distance from the center of the Earth to its surface, approximately 6.4 Γ 10^6 m.