Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Mass Transfer Coefficients
Unlock Audio Lesson
Today we are going to explore mass transfer coefficients. Why do you think these coefficients are crucial in engineering?
They help us understand how substances move between different phases, like gas and liquid.
Exactly! The mass transfer coefficient indicates the efficiency of this transfer. We rely on empirical correlations to estimate these coefficients, as direct measurement can be challenging.
What do you mean by empirical correlations?
Empirical correlations are essentially relationships formed from experimental data. They help predict coefficients based on factors like velocity and geometry.
So the more data we collect, the better our estimates will be?
Exactly! Good observation. Let's summarize the key points: mass transfer coefficients quantify how well substances transfer between phases, and empirical data plays a significant role in estimating these coefficients.
Factors Affecting Mass Transfer Coefficients
Unlock Audio Lesson
Now, let's dive deeper into what affects mass transfer coefficients. Can anyone think of a major factor?
I think velocity is important, isn't it?
Absolutely! Higher velocities generally enhance mass transfer. How about geometry? How does that play a role?
Different shapes can cause different flow patterns, which might affect transfer rates.
Correct! Geometry influences how fluids interact with surfaces. To remember, think of the acronym 'V-G-P', which stands for Velocity, Geometry, and Properties affecting mass transfer.
That's helpful! What else do we need to consider?
Concentration gradients are also crucial! They drive the transfer process, as higher gradients often lead to increased flux.
Flux Measurement and Concentration Gradient
Unlock Audio Lesson
Next, let's discuss how we measure flux and its relationship to concentration gradients. Why is this important?
Because we need to understand the rate at which mass is being transferred!
Exactly! The flux is the amount per unit area transferred and is influenced by the concentration gradient. Can anyone explain this further?
So when there's a higher concentration difference, the flux increases?
Right! That's why measuring the gradients accurately is crucial for calculating the coefficients.
What happens if the concentration isn’t uniform?
Great question! Non-uniform concentration can complicate measurements, often requiring assumptions of well-mixed conditions to simplify the analysis.
To summarize, understanding the relationship between flux and concentration gradients is vital for estimating mass transfer coefficients effectively.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The estimation of mass transfer coefficients is vital for predicting mass transfer rates in various environmental systems like lakes and air. This section emphasizes the reliance on empirical correlations derived from experimental data, focusing on the factors influencing these coefficients such as velocity, geometry, and concentration gradients.
Detailed
Estimation of the Mass Transfer Coefficients
In this lecture, Prof. Ravi Krishna explores the methods used to derive mass transfer coefficients critical for environmental quality monitoring. The core focus is on employing empirical correlations, which are established from experimental measurements under diverse conditions. These correlations relate the mass transfer coefficient (kA) to variables such as velocity, geometry, and the physical properties of the species involved. In particular, the section highlights how the concentration gradients across the interfaces during mass transfer influence the estimation process. It also addresses the interactions of gas and liquid phases, underscoring that empirical methods are practical when direct measurement is challenging. The lecture proposes methodological approaches using well-mixed conditions to ensure reliable flux measurements, ultimately aiming to derive coefficients applicable to real-world environmental scenarios.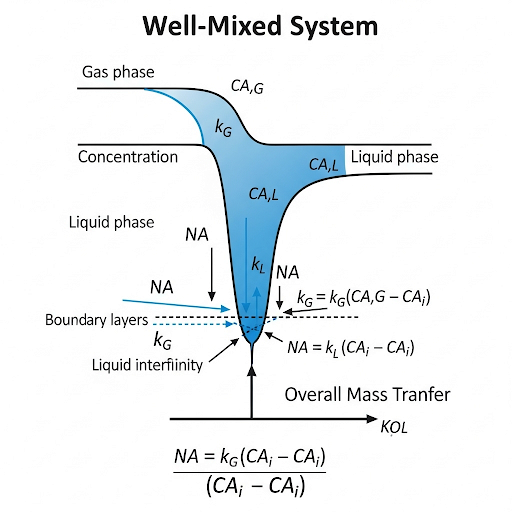
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Mass Transfer Coefficients
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, one has to get mass transfer coefficient, a measured mass transfer coefficient for different systems and the only a very efficient or practical way of doing it is by using empirical correlations. What does this mean? Empirical correlations mean there we are saying kA is a function of several things: velocity, geometry, and properties of various components.
Detailed Explanation
Mass transfer coefficients are crucial in various engineering applications. They quantify how effectively a substance moves from one phase to another, like from air to water. Instead of measuring these coefficients directly, engineers often rely on empirical correlations, which are equations derived from experimental data. These correlations link the mass transfer coefficient (kA) to various influential factors such as flow velocity, system geometry, and the physical properties of the materials involved.
Examples & Analogies
Consider making tea. The rate at which flavor from the tea leaves diffuses into the water is like the mass transfer coefficient. If you stir faster (like increasing velocity) or change the size of the tea leaves (like changing geometry), the flavor transfers more quickly. We use our past experiences (empirical data) to predict how fast the tea will brew.
Importance of System Definition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We are looking at wind speed mainly, this is v1. Then we are looking at the length of the section. Now, this is a very important concept, as mass transfer is occurring, concentration is changing across the interface.
Detailed Explanation
The definition of the mass transfer system is critical. Key parameters include wind speed and the length of the section where transfer occurs. As mass transfer takes place, the concentration of the transferred substance changes, affecting the efficiency of the transfer. Understanding these changes helps in accurately calculating the mass transfer coefficient because a longer path or higher speed can change the concentration gradients significantly.
Examples & Analogies
Think of it like a river flowing faster when it's narrow versus when it's wide. If you have a narrow and fast river (high velocity), the water can carry more leaves downstream quickly, while a wide slow river (low velocity) would allow leaves to settle. Similarly, in mass transfer, both speed and the path length influence how quickly something moves between phases.
Experimental Measurements and Variation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
What I have to do is I have to measure the mass transfer coefficient at every set of conditions. I will have different velocities of air, different lengths, and different diffusion coefficients.
Detailed Explanation
To accurately compute the mass transfer coefficients, experiments must be conducted under various conditions. This includes changing the velocity of air, the length of the transfer area, and the diffusion coefficients of the substances involved. Each of these factors influences how effectively mass transfer occurs.
Examples & Analogies
Imagine a cooking recipe where the temperature, time, and size of the ingredients can change the final dish. To get the best soup, you might need to try cooking it at various temperatures (velocity), in different pot sizes (length), or even using different vegetables (diffusion coefficients) to see what combination creates the best flavor.
Deriving and Utilizing Correlations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, the correlation may look like this for example. kA12 = α(v1)²(T)³(D)⁴. This will vary based on the system, like air side mass transfer coefficient for transfer across water air in a lake.
Detailed Explanation
Correlations are mathematical relationships that describe how mass transfer coefficients vary with changing conditions. An example equation might relate the mass transfer coefficient to factors like velocity, temperature, and diffusion. Understanding these correlations allows engineers to predict the mass transfer rates in different systems without conducting extensive experiments every time.
Examples & Analogies
Think of a recipe for a smoothie where the sweetness (mass transfer) depends on the type of fruit (velocity), ripeness (temperature), and other ingredients (diffusion factors). Just like knowing the right combination can help you make a delicious smoothie, understanding these correlations helps engineers optimize their processes.
Experimental Challenges and Solutions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The problem arises when measuring flux because we need to know the concentration gradient, which can be difficult to measure directly.
Detailed Explanation
In practice, measuring the flux (the rate of mass transfer) can be problematic due to difficulties in determining the concentration gradient. This gradient is essential for calculating the mass transfer coefficient. To overcome this, experiments are designed to manipulate conditions where some variables are known while others can be estimated based on established relationships.
Examples & Analogies
It's like trying to measure the speed of a car when you can't see the speedometer. You might use markers on the road to determine distance over time. In mass transfer, scientists find ways to estimate conditions even if some measurements are challenging.
Applying Correlation to Different Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When we looked at water evaporation, we observed that the maximum limit occurs when the system is a pure phase without any solute, making the concentration measurable.
Detailed Explanation
When dealing with pure substances in mass transfer experiments, the maximum efficiency occurs. In such cases, the concentration can be measured more easily, allowing for straightforward calculations of mass transfer coefficients. This understanding helps researchers design experiments that yield reliable and useful data.
Examples & Analogies
Imagine filling a glass with pure water and measuring how quickly it evaporates. The simple, clear setup with no complications allows us to easily see how temperature affects evaporation rates. Similarly, pure substances simplify mass transfer studies.
Real-world Application of Theory
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In field applications, researchers are often focused on obtaining data relevant to real-world environments, like lakes or rivers, and must scale their findings to apply to various chemicals.
Detailed Explanation
Field data collection is vital for validating laboratory findings. Researchers adapt the correlations obtained from controlled experiments to apply to real-world scenarios, which might involve different chemicals and conditions. This is often done by taking existing data and adjusting for specifics like chemical properties and environmental factors.
Examples & Analogies
Consider testing the effectiveness of a pesticide in a controlled environment, then needing to adjust your findings to apply to vast farmland. The field's conditions (different plants and weather) will affect how the pesticide works, thus requiring researchers to scale their experiments to account for real-world use.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Transfer Coefficient: A measure of how efficiently a substance transfers between phases.
-
Empirical Correlations: Relationships formed from experimental data to estimate mass transfer parameters.
-
Concentration Gradient: The difference in concentration across a phase that drives mass transfer.
-
Flux: The quantity of mass transferred per unit area, affected by concentration gradients.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An experiment measuring the evaporation of a solvent to derive the mass transfer coefficient based on the concentration of vapor in the air.
-
Using wind speed and surface area of water bodies to calculate the mass transfer coefficient for a lake's gas exchange process.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When mass moves fast and the sky is blue, the transfer coefficient tells us what to do!
📖 Fascinating Stories
-
Imagine a lake on a windy day. The water surface ripples, letting oxygen from the air transfer into the water quickly; that's how velocity affects mass transfer!
🧠 Other Memory Gems
-
Remember V-G-P for factors influencing mass transfer: Velocity, Geometry, and Properties.
🎯 Super Acronyms
FCD - Flux, Concentration Gradient, Diffusion are the keys to understanding mass transfer.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Empirical Correlation
Definition:
A mathematical relationship derived from experimental data to predict outcomes under various conditions.
-
Term: Mass Transfer Coefficient (kA)
Definition:
A parameter that quantifies the flux of a component per unit concentration gradient.
-
Term: Flux
Definition:
The rate of flow of mass through a surface per unit area.
-
Term: Concentration Gradient
Definition:
The rate of change of concentration in space, which drives mass transfer.
-
Term: WellMixed Condition
Definition:
A state where the concentration is uniform throughout a phase, often used in mass transfer analysis.