Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to No-Slip Conditions
Unlock Audio Lesson
Today, we're going to discuss an important concept in fluid mechanics known as the no-slip condition. Can anyone explain what you think happens when a fluid touches a solid surface?
Does the fluid move at the same speed as the surface it's touching?
Exactly! This phenomenon means that the fluid particles right at the surface have zero velocity if the surface is stationary, or they match the surface's velocity if it moves. This is what we call the no-slip condition. Can someone remind me what this translates to in practical terms?
It affects how we calculate flow in pipes and other systems, right?
Correct! The no-slip condition is crucial for calculating shear stress and understanding velocity profiles. Remember, it leads to different fluid behavior based on proximity to the solid surfaces.
So, if I understand correctly, the fluid starts at zero velocity and increases as you move away from the surface?
Absolutely! This gradient helps us predict how fluid flows in various applications. Let's remember this with the acronym 'Velocity Equals Surface' or 'VES' to represent that fluid velocity equals surface velocity at the boundary.
I like that! It makes it easier to remember.
Good! In summary, the no-slip condition illustrates how fluid interfaces with solid boundaries, impacting our study and application of fluid dynamics.
Implications of No-Slip Conditions
Unlock Audio Lesson
Now let's discuss what the no-slip condition means for engineers. Why do you think accurately modeling this condition is essential?
It helps us design better systems that can handle fluid flow, like pipelines!
Correct! Understanding no-slip conditions allows us to optimize flow rates and minimize energy losses. What about in other fields, such as aerodynamics?
I think it would influence how air flows over wings and affects lift.
Exactly! That's a fantastic application. The no-slip condition helps us design better aerodynamic shapes, especially in vehicles and aircraft to reduce drag. Remember, the principle can also be applied in natural systems like rivers!
It sounds like knowing how fluids behave can help prevent disasters too.
Absolutely! Understanding this can prevent problems in systems that rely on fluid mechanics. Let’s create a mnemonic, 'Fluid Flow Follows Solid,' to remember that fluids adhere to solid surfaces under flow conditions.
That's catchy! It will help.
To summarize, the implications of the no-slip condition extend to numerous real-world applications, reinforcing why understanding this concept is essential for fluid dynamics.
Practical Examples and Applications
Unlock Audio Lesson
Let's explore some practical examples of the no-slip condition. Can anyone share where they've seen this in action?
In water flowing through pipes! Like when you turn on a faucet.
Great example! The water sticks to the pipe surface, and the velocity increases as it moves away. What else?
How about the way wind interacts with a building’s surface?
Absolutely! The wind's behavior changes near the structure due to the no-slip condition, which affects things like pressure calculations. We apply this concept to ensure proper designs can withstand forces from wind.
It seems important for ensuring safety!
Precisely! Lastly, let’s visualize using our virtual fluid balls concept. What if we visualize the fluid particles as balls when it comes into contact with a solid surface?
Each ball would stop moving at the surface and then pick up speed as they flow away!
Exactly! And this visualization aids our understanding of how particles behave under different conditions. To recap, no-slip conditions have numerous implications for practical applications, providing critical insight into fluid behavior.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
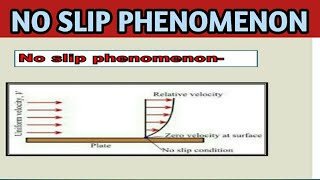
The no-slip condition is a fundamental aspect of fluid mechanics that states fluid particles in contact with a solid surface move with the same velocity as the surface. This section elaborates on its significance and implications for fluid flow dynamics.
Detailed
Detailed Summary
The no-slip condition is a crucial concept in fluid mechanics that asserts that when a fluid flows against a solid surface, the fluid particles at the interface have the same velocity as the surface itself. This principle is essential for understanding fluid behavior near boundaries and plays a vital role in various applications across engineering and science.
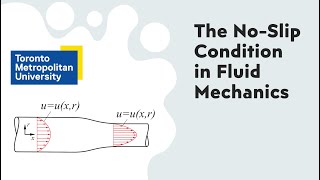
When fluids are in contact with a stationary solid surface, the fluid layers adjacent to the surface experience a velocity of zero. As one moves away from the surface, the fluid velocity gradually increases until it reaches a uniform value in the flow far away from the solid boundary. This velocity gradient is a result of viscous forces at play near the interface, leading to shear stress and influencing how fluids behave in real-world scenarios such as in pipelines, around aircraft wings, and in natural water bodies.
Additionally, this section introduces the concept of virtual fluid balls to help visualize fluid flow patterns, particularly regarding shear stress and how it influences the behavior of the fluid. Understanding no-slip conditions is pivotal in the analysis and simulation of fluid dynamics, making it a foundational principle in fluid mechanics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding No-Slip Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When a fluid flows through an interface with a solid surface, the condition that prevails is known as no-slip conditions. For example, if I have a plate at rest (velocity = 0) and uniform flow coming from the left, fluid particles that touch the surface will have the same velocity as the plate, which is zero. As you move away from the surface, the fluid's velocity increases.
Detailed Explanation
No-slip conditions indicate that the velocity of a fluid in direct contact with a solid surface is equal to the velocity of that solid surface. This means that if a plate is stationary, the fluid particles right at the surface will not move (velocity = 0). As you get further from the surface, the velocity gradually increases until it matches the uniform flow speed. This gradient of velocity change is crucial in understanding how fluids interact with solid surfaces.
Examples & Analogies
Imagine sliding down a water slide. The point where the water touches the slide (the surface) is slow because it's 'stuck' to the slide. But as you move away from the surface, the water speeds up until you feel it pushing you down faster. That’s similar to how fluid velocity changes near a stationary pipe or boundary.
Impact of No-Slip Conditions on Velocity Distributions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
With no-slip conditions, the velocity distribution changes along the surface from zero at the solid boundary to a maximum value at some distance away. For example, if I have a blunt nose of an aerofoil with fluid flowing over it, the fluid's velocity starts at zero at the surface and increases as you move away, leading to varying distributions.
Detailed Explanation
The varying velocities due to no-slip conditions lead to a velocity profile, where the flow velocity is highest farthest from the surface. This profile is essential in designing aerofoils, as understanding how air moves around them affects lift and drag forces. By visualizing velocity distributions, engineers can optimize shapes for better performance.
Examples & Analogies
Think of a crowd of people walking in a hallway. If everyone starts at a halted entrance (the surface, where there's no movement), people closest to the door will start moving first, while those deeper in the crowd take longer to reach the exit. Just like in fluid flow, those closer to the surface gain speed as they move away from the obstruction.
Flow Separations and No-Slip Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When considering a curved surface in fluid flow, there can be points where fluid particles detach from the surface, indicating that no-slip conditions do not apply at those spots. This separation leads to different flow patterns and must be accounted for in complex fluid dynamics.
Detailed Explanation
In scenarios such as air flowing over a curved wing, at certain points, the fluid can no longer adhere to the surface due to inertial forces becoming too great, leading to flow separation. This phenomenon can significantly impact performance, causing drag and reducing efficiency. Understanding where and why separations occur is crucial in aerodynamics.
Examples & Analogies
Imagine a car speeding up a hill. At some point, if the incline is steep enough, the air cannot 'stick' to the car’s surface anymore; it 'breaks away'. This detachment is similar to flow separations in fluid dynamics, where the vehicle’s shape influences how efficiently it travels through the air.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
No-Slip Condition: Fluid particles at a boundary move with the same velocity as the solid surface.
-
Velocity Gradient: The gradual increase in fluid velocity as one moves away from a solid surface.
-
Shear Stress: The stress parallel to the surface due to fluid's viscosity and motion.
-
Virtual Fluid Balls: A tool to illustrate and visualize fluid motion and behavior.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Water flowing through a pipe where it adheres to the inner surface, illustrating no-slip conditions.
-
Wind flowing over a car body, showing variations in pressure and speed due to the no-slip effect.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
At the wall, the flow stands still, / Matching speed, like a flow of thrill.
📖 Fascinating Stories
-
Imagine a river flowing next to a rocky shore. As it hits the rock, the water sticks momentarily before speeding off again, representing how the water adheres to the solid due to the no-slip condition.
🧠 Other Memory Gems
-
Think 'Velocity Equals Surface' (VES) to remember that fluid velocity equals the surface's velocity at the boundary.
🎯 Super Acronyms
VES - Velocity Equals Surface
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: NoSlip Condition
Definition:
A principle in fluid mechanics stating that fluid at a solid boundary has the same velocity as the boundary.
-
Term: Velocity Profile
Definition:
The variation of flow velocity in a fluid, particularly near boundaries where the no-slip condition applies.
-
Term: Shear Stress
Definition:
The stress component parallel to the surface, resulting from the fluid's viscosity.
-
Term: Viscous Forces
Definition:
Forces caused by the viscosity of fluids, influencing motion and creating resistance to flow.
-
Term: Virtual Fluid Balls
Definition:
A visualization concept where fluids are represented by moving balls to illustrate fluid behavior and flow.