Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Systems vs. Control Volumes
Unlock Audio Lesson
Today, we'll begin by understanding the difference between a system and a control volume. Can anyone tell me what a system is?
Isn't a system just a fixed quantity of matter we study, like a gas in a cylinder?
Exactly! A system has fixed mass and boundaries. Now, what about a control volume?
I think a control volume is a region in space defined for analysis, right?
Spot on! Control volumes can be flexible in time and space. Can someone recall why we often prefer control volumes in fluid mechanics?
It’s because we can easily account for mass and energy that flows in and out!
Exactly! That ability helps simplify complex flow problems. Great job summarizing!
Flow Analysis Techniques
Unlock Audio Lesson
Now, let's explore the methods available for flow analysis. Can anyone name them?
There are experimental, analytical, and computational methods!
Right! Let’s discuss each one briefly. What do you think experimental methods involve?
I think it involves using models in wind tunnels to measure fluid parameters?
That's correct! Now, can anyone explain what we do in analytical methods?
In analytical methods, we apply conservation equations to derive properties like velocity and pressure.
Excellent! And how about computational methods?
We use computers to solve sets of non-linear equations numerically to find fluid characteristics.
Great summary! Each method has its pros and cons, and knowing when to apply them is key.
Importance of Conservation Laws
Unlock Audio Lesson
Lastly, let’s discuss the conservation laws. Can anyone name the three primary conservation laws we use in fluid dynamics?
Mass conservation, momentum conservation, and energy conservation!
Correct! Why do you think these laws are so crucial?
They help us understand how fluid interacts with forces and boundaries, right?
Exactly! These laws guide us in setting up our mathematical models effectively. Who can summarize how they’re applied in the analytical and computational approaches?
In analytical methods, we derive equations using boundary conditions, while in computational methods, we solve differential equations integrating these laws.
Fantastic! Understanding these conservation laws is essential for any engineer working with fluid mechanics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the concepts of systems vs. control volumes in fluid mechanics, various flow analysis techniques including experimental, analytical, and computational approaches, and the significance of applying conservation laws for solving complex fluid dynamics problems.
Detailed
Computational Fluid Dynamics
In this section, we delve into the realm of Computational Fluid Dynamics (CFD), a field critical for analyzing complex fluid flow scenarios. We start by distinguishing between two principal approaches in fluid mechanics: systems and control volumes. A system is defined as a quantity of matter in a specified region, usually fixed in mass, while a control volume is a designated space through which fluid mass and energy can move in and out.
Next, we consider flow analysis techniques. When confronted with complex fluid behaviors, engineers can employ three primary methods:
1. Experimental Methods: These involve creating scaled models and conducting wind tunnel tests to measure parameters like velocity and pressure.
2. Analytical Methods: This approach utilizes equations of conservation (mass, momentum, energy) to deduce properties in a fluid flow, often yielding simplified results based on certain assumptions.
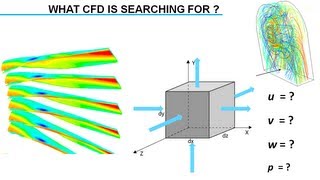
3. Computational Methods: With advances in technology, CFD has gained prominence. This involves solving sets of non-linear partial differential equations numerically to approximate the velocity, pressure, and density fields in fluid flow, enabling detailed predictions of system behavior.
The section highlights that understanding these aspects allows engineers to approach complex fluid problems strategically by knowing which technique to apply based on the problem's nature.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Three Approaches to Solve Fluid Flow Problems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, if you look it the next very interesting problems what I have to give a illustrations to you that if you look at this very beautiful bird sitting on a branch. If there is a wind movement is coming from this and this wind movements consider let me the this speed is increasing from 10 km/hr to 50 km/hr, okay. The speed of the wind is increasing from 10 km to 50 km/hr. The question which comes it at which speed this bird cannot hold this branch. That means after that critical speed this bird has to fly from this place okay that is very interesting topic what you can understand it. That means what we are looking it that there is a fluid flow is coming from these sides is having a speed let be the V the speed is what is coming upon that. Because of that here you are going to have a two force components okay. One will be the drag force and other will be the lift force and will have a resultant force what is occurring, because this fluid where it is passing through that that what will create a flow structure such a way that there will be a drag force there will be the lift force.
Detailed Explanation
In Computational Fluid Dynamics (CFD), we often analyze how objects, like our bird example, interact with fluid flows such as wind. As the speed of wind increases, the bird experiences differently directed forces (drag and lift). The drag force opposes the motion of the bird against the wind, while lift acts upward, counteracting gravity. The fundamental aim is to find the critical wind speed where the lift force is no longer sufficient to keep the bird on the branch. By understanding these forces, we can predict at what point the bird will need to fly away. This introduces the concept of computational analysis, where we compute these forces using mathematical and numerical techniques, considering variables like fluid velocity and force interactions.
Examples & Analogies
Imagine riding a bike against a strong wind. As you pedal faster, you need to angle your body to reduce the wind's drag on you. At a certain wind speed, it might become too hard to stay upright on the bike and maintain balance. Similarly, the bird on its branch must consider the wind's force. If the wind is too strong (like when riding at high speeds), it can’t stay resting on the branch anymore; it has to take off and fly. This everyday experience helps us understand the forces of lift and drag in a real-world context.
Methods for Analyzing Fluid Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So we can conduct the experimental way to compute it what will be the drag force, what will be the lift force, what will be the resultant forces or we can follow a analytical methods. That means we can follow laws of conservations like mass conservation, momentum conservation, energy conservation, then we take a appropriate control volumes. Then we try to find out what could be the approximate the drag force and the lift force on this case. Or we go for very much the computational methods.
Detailed Explanation
There are three primary ways to analyze fluid flow: empirical (experimental), analytical, and computational. Experimental methods involve creating physical models, measuring fluid dynamics in a wind tunnel or similar setups. Analytical methods apply physical laws (like conservation equations) mathematically to simplify and derive equations for drag and lift without experimentation. Lastly, computational methods use powerful computers to solve complex sets of equations numerically, providing an approximation of fluid behavior around objects. Each method has its own applications depending on the complexity and requirements of the problem being analyzed.
Examples & Analogies
Think of a chef trying to perfect a new recipe. They might first experiment (use an experimental method), making the dish multiple times, adjusting ingredients and cooking times based on taste tests. If they understand the science behind cooking (like boiling point variations), they might apply that knowledge theoretically (the analytical method) to predict how changes can affect the dish without making it again. Finally, using advanced cooking tools or programs that predict cooking outcomes (similar to computational methods), they can experiment virtually with different variables before actually cooking. All methods are valuable, and each offers insights depending on the chef’s goal.
Computational Fluid Dynamics Overview
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In which what we do it any of the fluid problems okay, we define through these mass conservations and momentum, energy conservation into a set of partial differential equations. This most often is a nonlinear partial differential equations and both equations we try to solve the numerically.
Detailed Explanation
Computational Fluid Dynamics involves the transformation of fluid flow problems into mathematical forms, specifically a set of partial differential equations (PDEs) that describe the conservation of mass, momentum, and energy. Since these equations are typically nonlinear, they require numerical methods for solutions rather than analytical exact methods. This means the equations won't always yield straightforward answers; instead, we use computational algorithms to approximate the variables like pressure, velocity, and density distributions in the fluid flow. Understanding these approximations is crucial as they provide insights that guide design and engineering solutions.
Examples & Analogies
Consider a traffic flow simulation where engineers want to solve how cars move through city intersections. The complexity involves thousands of variables (car speeds, traffic lights, pedestrian movement), and it can’t be easily analyzed with simple math. Instead, computer programs convert this complex scenario into equations and approximate solutions. Just like how traffic simulations help manage real-life intersections, CFD does the same for engineers working on fluid dynamics, helping predict behaviors of fluids in diverse applications, from airplane wings to water treatment systems.
Summary of Fluid Flow Solutions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you let me summarize that way, there are three basic ways to solve the problems. One is a bigger control volume where we have an integral analysis or the analytical methods ways. You take a smaller control volume, which is very close to infinitely small. Then you get a set of a differential equation problem.
Detailed Explanation
To summarize, there are three primary approaches in fluid dynamics: using larger control volumes to apply integral analysis (analytical methods), smaller control volumes for differential analysis (providing more detailed results), and experimental methods that validate both approaches. The choice among these methods depends on the situation's complexity, available resources, and the specific requirements of the analysis. Understanding which approach to use, and being able to switch between them, is crucial for modeling and solving fluid flow challenges effectively.
Examples & Analogies
Think of conducting a survey about people's eating habits. You could look at large sections of the population (bigger control volumes) to get a general idea, which is easier but less precise. Alternatively, you could focus on small details, like specific families or individuals (smaller control volumes), leading to more accurate data but requiring more effort to gather. Lastly, you could try the survey face-to-face (experimental methods) to validate your findings. Each technique provides different insights and serves specific purposes, just like the fluid flow solutions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Fluid Flow Analysis: Techniques employed to solve fluid dynamics issues, emphasizing how to apply different methods appropriately.
-
Use of Control Volumes: The relevance of defining a control volume for easier analysis of fluid systems.
-
Conservation Laws: Key principles that must be applied when dealing with fluid flow problems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Analyzing the airflow around a bird to determine the speed at which it can hold onto a branch despite increasing wind speeds.
-
Using scaled models in a wind tunnel to measure drag forces acting on structures like weather radar towers in varying wind conditions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To see how fluids flow, conservation's the way to know.
📖 Fascinating Stories
-
Imagine a bird holding tight to a branch, fighting against the wind. This illustrates the dynamic interplay of forces—drag and lift—shaped by fluid flow.
🧠 Other Memory Gems
-
CAD: Control volume, Analytical methods, Drag force to remember key elements in fluid dynamics.
🎯 Super Acronyms
FEM
- Fluid Experimental Modeling
- reminding us of physical testing in fluid analysis.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: System
Definition:
A fixed quantity of matter or region in space chosen for study in fluid mechanics.
-
Term: Control Volume
Definition:
A defined space in fluid mechanics through which fluid can flow in and out.
-
Term: Experimental Methods
Definition:
Techniques that utilize scaled models and physical experiments to analyze fluid behavior.
-
Term: Analytical Methods
Definition:
Approaches that apply conservation equations to derive properties of fluid flow.
-
Term: Computational Methods
Definition:
Numerical techniques for solving fluid dynamics problems using computers.
-
Term: Conservation Laws
Definition:
Fundamental principles that describe the conservation of mass, momentum, and energy in fluid systems.
-
Term: Velocity Field
Definition:
A representation of the velocity of fluid particles in a given flow.
-
Term: Pressure Field
Definition:
A representation of the pressure exerted by fluid at various points in a flow.
-
Term: Density Field
Definition:
A representation of the density of fluid at various points in a flow.