Basics of Fluid Mechanics – II
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Fluid Kinematics and Velocity Field
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we’re focusing on fluid kinematics, particularly the velocity field. Can anyone explain what we mean by the velocity field?

Isn't it how fast the fluid is moving in different directions?

Exactly! We can think of the fluid as made up of tiny particles; thus, we can describe the velocity of these particles as a function of their location in space. This leads us to the continuum assumption.

Can you elaborate on the continuum assumption?

Certainly! The continuum assumption means we treat fluids as continuously distributed matter, which allows us to use calculus to describe how properties like velocity change over space and time.

How is velocity represented in the equations?

Great question! We often denote fluid velocity as a vector V = (u, v, w), where u is the velocity in the x-direction, v in the y-direction, and w in the z-direction. Each of these can depend on spatial coordinates and time.

So does that mean the velocity can change depending on where you are in the fluid?

Correct! This is crucial when looking at complex flows. Remember, understanding these concepts forms the foundation for analyzing fluid behavior.

To summarize, the velocity field gives us a snapshot of how fluid moves based on its location and time. Keep this in mind as we move deeper into fluid dynamics.
Eulerian and Lagrangian Descriptions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, we need to understand two major approaches to fluid mechanics: Eulerian and Lagrangian descriptions. Who wants to start off?

I've heard you mention Eulerian before. What is it exactly?

The Eulerian method describes fluid flow from fixed points in space, focusing on how properties like velocity and pressure change at these locations over time.

And what's the Lagrangian method then?

In contrast, the Lagrangian method follows individual fluid particles, observing how their properties evolve as they move. This means we view the flow from the perspective of the particle itself.

So it's like being on a ride with a particle?

Exactly! Think of it as tagging a particle and analyzing its journey through the fluid. Does anyone see the benefits of each approach?

I'm thinking Eulerian could be useful for many fluids flowing over an area.

And Lagrangian must be great for understanding complex particle behavior.

Spot on! Each method has its applications depending on what you need to analyze, whether it's flow patterns or individual particle dynamics.

To summarize, understanding the differences between these methods helps us choose the correct approach for fluid analysis based on the problem.
Dimensionality of Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's discuss the dimensionality of fluid flow. How many dimensions can fluid flows exist in?

Usually three, right? x, y, and z?

That's correct! However, sometimes we can simplify by assuming two or even one-dimensional flow. Can someone explain when that might happen?

If one of the velocity components is very small?

Exactly! If one component is negligible compared to others, we might treat the flow as two-dimensional. Can you think of real-world examples?

Airflow over a flat surface could be treated as two-dimensional since vertical motion might be minimal.

Excellent example! It’s essential to understand these simplifications for practical flow analysis.

To summarize: flows can often be complex and three-dimensional, but simplifications can help in practical analysis based on negligible velocity components.
Steady vs. Unsteady Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Finally, let's discuss steady and unsteady flow. Who can tell me the difference?

Um, steady flow doesn't change with time, right?

Perfect! In steady flow, flow parameters remain constant over time. On the other hand, unsteady flow changes with time. Can you give an example of unsteady flow?

Maybe water flowing from a tap, where it starts and stops?

Exactly! Changes in time make the flow exhibit unsteady characteristics. What about steady flow?

I guess something like water flowing through a constant-width pipe?

Great observation! Steady flows align well in many practical fluid mechanics scenarios.

So to wrap up, steady flows maintain constant parameters over time, while unsteady flows change continually.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section introduces fluid kinematics, focusing on the velocity field, the continuum assumption, and how fluid properties can vary with spatial coordinates. It distinguishes between Eulerian and Lagrangian flow descriptions, detailing the behavior of fluid properties in relation to time and space.
Detailed
Detailed Summary
In this section titled Basics of Fluid Mechanics – II, we explore fundamental concepts associated with fluid kinematics, emphasizing the velocity field. The continuum assumption is pivotal here, enabling us to treat fluids as made up of infinitesimal particles, thus allowing for a mathematical characterization of properties such as density, pressure, velocity, and acceleration as functions of spatial coordinates (x, y, z) and time (t).
Key topics include:
- Velocity Field: The fluid velocity is expressed in terms of its x, y, and z components (u, v, w), which can depend on spatial coordinates and time, forming a vector field. Each component represents the velocity in its respective direction.
- Eulerian vs. Lagrangian Descriptions: We differentiate between two primary methodologies to analyze fluid flow: the Eulerian method, which observes properties at fixed points in space, and the Lagrangian approach, which follows individual fluid particles over time, noting how their properties change.
- Dimensionality of Flow: Fluid flows can be three-dimensional, two-dimensional, or even one-dimensional depending on the flow characteristics. The significance of analyzing flows in different dimensions is highlighted, especially in situations where one or two velocity components may be negligible.
- Steady vs. Unsteady Flow: The section concludes with a discussion on the nature of flow being either steady (where flow properties remain constant over time) or unsteady (where they change with time). This is crucial in fluid mechanics as it influences the stability and behavior of fluid systems.
Such foundational concepts are essential in hydraulic engineering and applications dealing with fluid dynamics.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Fluid Kinematics
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Welcome back to this course of hydraulic engineering. This week, we are going to cover basics of fluid mechanics, this is the second week of this. So, we call this basic of fluid mechanics II the first topic in this series is going to be fluid kinematics.
Detailed Explanation
In this introduction, the focus shifts to fluid kinematics, a fundamental aspect of fluid mechanics. Fluid kinematics studies the motion of fluids (liquids and gases) without considering the forces that cause them to move. This foundational concept sets the stage for understanding more complex phenomena in fluid dynamics, allowing students to explore how fluids behave under various conditions.
Examples & Analogies
Think of fluid kinematics like tracking a moving car on a road. While observing the speed and direction of the car, we don't need to consider how the engine works or how fuel is consumed; we focus solely on the car's motion.
Velocity Field Concept
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
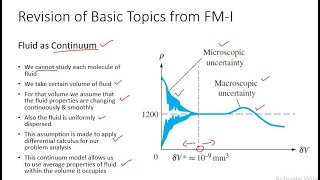
We will talk about the velocity field. The fluids can be assumed to be made up of infinitesimal small particles and they are tightly packed together. This is implied by the continuum assumption.
Detailed Explanation
The velocity field refers to how the velocity of fluid particles varies in space at any given moment. The continuum assumption suggests that fluids can be treated as continuous media rather than individual particles. This simplification allows us to describe properties such as velocity, pressure, and density as functions of position and time, making it easier to analyze fluid behavior in different scenarios.
Examples & Analogies
Imagine a crowded highway where every car represents a fluid particle. Just as we can analyze how fast each car is moving and in which direction, we analyze fluid velocities at different points in space to understand overall flow.
Representation of Fluid Properties
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Properties such as density, pressure, velocity, and acceleration may be given as a function of the fluid's location.
Detailed Explanation
This statement highlights that essential properties of fluids are not uniform but vary with location. Density might change due to pressure differences, for instance. By analyzing these properties as functions of spatial coordinates (x, y, z), we can understand how the fluid behaves in different physical contexts. This is crucial for solving problems in hydraulic engineering and fluid dynamics.
Examples & Analogies
Picture yourself exploring a swimming pool. In one corner, the water might feel warmer (different density) due to sunlight exposure, while in deeper areas, the water pressure increases. Each location in the pool represents different fluid properties that affect how you swim.
Eulerian vs. Lagrangian Flow Descriptions
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
There are two most famous descriptions of the flow: Eulerian and Lagrangian. In the Eulerian method, fluid motion is given by prescribing properties as a function of space and time.
Detailed Explanation
The Eulerian approach focuses on specific points in space and studies how fluid properties evolve at those points over time. This method is useful for most engineering applications, where measuring properties at fixed locations is more manageable. On the other hand, the Lagrangian approach follows individual fluid particles, observing how their properties change as they move. Understanding these two perspectives is crucial for comprehending fluid mechanics.
Examples & Analogies
Consider a sports event. The Eulerian method is like watching the game from the stands, seeing how players interact at various points on the field. The Lagrangian method is like being on the field, following a single player throughout the game to see how their performance changes over time.
Types of Flows: Steady vs. Unsteady
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In steady flow, the fluid flow conditions at any point do not change with time. In unsteady flow, the flow parameters at any point change with time.
Detailed Explanation
The distinction between steady and unsteady flow is crucial in fluid mechanics. In steady flow, the velocity and other properties at a fixed point remain constant over time, making analysis simpler. In contrast, unsteady flow means that properties are constantly changing, requiring more complex mathematical models to describe the behavior of the fluid. Recognizing the characteristics of each flow type allows engineers to select appropriate methods for analyzing fluid systems.
Examples & Analogies
Imagine a river flowing steadily; you can predict the water level and speed at specific spots (steady flow). Now think of a river where rainfall causes the water level to rise and fall unpredictably (unsteady flow), making it challenging to assess flow conditions accurately.
Key Concepts
-
Continuum Assumption: Treating fluids as continuously distributed matter.
-
Velocity Field: The representation of fluid speed at different points in space.
-
Eulerian Method: Describing fluid properties at fixed points.
-
Lagrangian Method: Tracking individual fluid particles.
-
Dimensionality of Flow: Discussing three-dimensional to one-dimensional flows based on velocity components.
-
Steady Flow: Parameters remain constant over time.
-
Unsteady Flow: Parameters vary with time.
Examples & Applications
Air flowing over an airplane wing can exhibit three-dimensional flow characteristics due to varying velocities in different directions.
Fluid flow from a faucet can show unsteady flow when the water begins to dribble out and then stops.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Fluid flows in three ways, 3D or just in 2 plays; follow particles, see them shift, Euler or Lagrange, they both uplift.
Stories
Imagine a river, three-dimensional with fish swimming around. Some fish move fast, others slow. Sometimes the flow changes with the tides; that's steady and unsteady, respectively.
Memory Tools
E-L-D-S: E for Eulerian, L for Lagrangian, D for dimensionality, S for steady/unsteady flow.
Acronyms
F-R-E-S-H
for flow
for Reynolds (number)
for Eulerian
for steady
for height (pressure). This helps remember fluid flow concepts.
Flash Cards
Glossary
- Velocity Field
A representation of fluid velocity at various points in a defined spatial area, expressed as a vector field.
- Continuum Assumption
The approximation that a fluid is composed of continuous matter rather than discrete particles.
- Eulerian Flow Description
A method of analyzing fluid flow by observing changes at fixed points in space.
- Lagrangian Flow Description
A method of analyzing fluid flow by following individual fluid particles over time.
- Dimensionality of Flow
Refers to whether a fluid flow is three-dimensional, two-dimensional, or one-dimensional based on the negligible velocity components.
- Steady Flow
A condition where fluid flow parameters do not change with time.
- Unsteady Flow
A condition where fluid flow parameters change with time.
Reference links
Supplementary resources to enhance your learning experience.
