Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Uniform Flow
Unlock Audio Lesson
Let's begin our discussion on uniform flow. Can anyone tell me how we define uniform flow in fluid mechanics?
Is it when the fluid properties, like velocity, don’t change over time?
Close! In uniform flow, properties are constant not just over time, but across space as well. This means that at any given moment, the velocity or other hydrodynamic parameters are the same at all points in the flow field.
So, it doesn't matter where you measure it in that flow, you always get the same value?
Exactly! And this is why uniform flow is an essential concept in fluid mechanics. We can express this mathematically as velocity being a function of time only, like V(t).
Could you give an example where we might see uniform flow?
A stream with a constant depth and width flowing steadily would be an example. Now, let's summarize: uniform flow means no change in fluid properties across space. Remember: U for Uniform - No Variance!
Exploring Non-Uniform Flow
Unlock Audio Lesson
Now let’s shift our focus to non-uniform flow. What do you think characterizes this type of flow?
Is it when the velocity and other properties change from point to point?
Correct! During non-uniform flow, the fluid properties vary depending on the position within the fluid. This can happen in various directions, both along and perpendicular to the flow.
So, it’s opposite to uniform flow, right?
Precisely! Non-uniform flow is indeed the opposite. For example, you will see non-uniform flow near solid boundaries where the flow velocity tends to decrease to zero adjacent to the boundary, due to viscosity.
What’s the term for that effect again?
That phenomenon is called the no-slip condition. It’s key to understanding why the flow isn’t uniform near surfaces. In summary, non-uniform flow indicates variability with position. U for Uniform, and then think 'N for Non—change!'
Streamlines in Fluid Flow
Unlock Audio Lesson
Next up is an important concept! Who can tell me what a streamline is in fluid flow?
Is it like a line that shows the direction of flow at every point?
Exactly! A streamline is a continuous line drawn such that it is tangential to the velocity vector at every point. This helps visualize the flow.
How is that useful?
It's useful because it helps us analyze the flow field without having to track every particle. It simplifies the understanding of how flow moves around different geometries. Remember this: 'Every streamline gives a suggestion; flow direction and velocity - it’s a reflection!'
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces the concepts of uniform and non-uniform flows in fluid mechanics. Uniform flow is characterized by consistent velocity and hydrodynamic parameters across space, whereas non-uniform flow exhibits variations depending on position. Understanding these concepts is essential for further studies in fluid dynamics, particularly in analyzing open channel flows.
Detailed
Uniform and Non-Uniform Flows
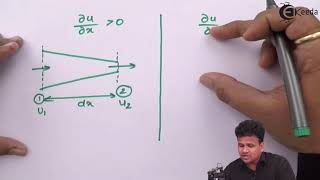
In this section, we explore the concepts of uniform and non-uniform flows. Uniform flow is defined by consistent velocity and hydrodynamic properties across the flow field, meaning these properties do not vary with the position of the fluid particles. Essentially, it highlights a scenario where the fluid flow is dependent solely on time, not influenced by spatial distribution. This concept is pivotal as it sets a foundation for analyzing more complex fluid behaviors.
In contrast, non-uniform flow is characterized by variability in velocity and other hydrodynamic parameters from point to point in the flow field. The changes may occur either in the flow direction or perpendicular to it, indicating that fluid properties adjust based on location. This non-uniformity is particularly prominent near solid boundaries where velocity profiles often change, exemplifying real-world applications like riverbanks or pipes. The insights on flow between steady/unsteady and uniform/non-uniform conditions will aid in further studies of open channel flows and fluid dynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Uniform Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, uniform flow is defined when the flow field, that is, the velocity and other hydrodynamic parameters do not change from point to point. In a steady flow, these properties do not change with respect to time; in uniform flow, they do not change with respect to space at any instant of time.
Detailed Explanation
In uniform flow, the characteristics of the fluid, such as velocity and pressure, remain constant across different points in the flow field. This means if you measure these properties at various points within the flow, you will get the same values. Unlike steady flow, which remains unchanged over time, uniform flow remains unchanged across space. In simpler terms, if you were to take a sample of fluid from any point, it would feel the same in terms of these parameters.
Examples & Analogies
Imagine a straight river flow that is wide enough so that the water flow is consistent from one bank to the other. If you take a cup of water from different spots in that stretch of the river, the water will taste the same and flow at the same speed. This is an example of uniform flow.
Implications of Uniform Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Implications for a uniform flow; there will be no spatial distribution of hydrodynamic and other parameters, as we told, because the parameters really does not depend upon the location.
Detailed Explanation
When we say there is no spatial distribution in uniform flow, it means that regardless of where you measure within the flow area, you'll obtain the same value for any hydrodynamic parameter, such as velocity or pressure. This concept helps engineers and scientists understand and predict how fluids behave under specific conditions, simplifying calculations and designs.
Examples & Analogies
Think of a perfectly crafted chocolate fountain. The chocolate flows smoothly and uniformly around the fountain; if you dip a spoon at any place, you'll get the same richness and temperature of chocolate, reflecting the uniformity in flow.
Introduction to Non-Uniform Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Non-uniform flow occurs when the velocity and other hydrodynamic parameters change from one point to the other, which is the opposite of uniform flow.
Detailed Explanation
In non-uniform flow, the fluid's characteristics vary with different points in space. This means that if you take measurements at various locations, you'd get different values. Non-uniform flow typically happens in situations where there are obstacles, changes in the channel geometry, or variations in other external factors affecting the fluid dynamics.
Examples & Analogies
Consider a river that flows past a rocky area. Here, the flow speed changes as the water encounters rocks that create turbulence. If you were to measure the flow speed at various points along the river, you would notice significant variations; this exemplifies non-uniform flow.
Characteristics of Non-Uniform Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Important points for a non-uniform flow include that the changes with position may occur in the direction of flow or in a direction perpendicular to it.
Detailed Explanation
Non-uniform flow can change not just along the direction that the fluid is flowing but also at angles to this direction. This complex behavior means that hydraulics engineers must consider both the flow direction and the perpendicular factors when analyzing how fluid moves through a system.
Examples & Analogies
Imagine a basketball being passed around in a crowded gym. The ball's velocity changes as it moves differently depending on who catches it, where they are positioned, and how they throw it. This is similar to non-uniform flow, where multiple factors cause changes in speed and direction within the fluid.
Effects Near Solid Boundaries in Non-Uniform Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Non-uniformity in a direction perpendicular to the flow is always encountered near solid boundaries past which the fluid flows.
Detailed Explanation
As fluid flows near solid boundaries (like river banks or pipe walls), friction and other effects cause the fluid velocity to change, creating a non-uniform flow profile. The particles of fluid closest to the boundary tend to move slower than those further away due to this interaction.
Examples & Analogies
Think of swimming near the edge of a swimming pool. When you get close to the wall, the water feels different because the motion is constrained by the wall, making it harder to swim smoothly. This analogy outlines how fluid flow near solid boundaries creates varying velocities.
The No-Slip Condition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
All fluids possess viscosity. Viscosity can be viewed as friction in fluids, and because of this friction, the relative velocity of the fluid at the wall is reduced to zero, a condition known as the no-slip condition.
Detailed Explanation
The no-slip condition is a crucial concept in fluid dynamics stating that at the boundary (like the edge of a pipe or a solid object), the fluid doesn't slide over the surface; instead, it sticks to it. This means that the amount of liquid closest to the surface is at rest, while fluid layers further away can flow freely. This condition leads to velocity variations and contributes significantly to the analysis of non-uniform flow profiles.
Examples & Analogies
Think of honey spreading on a piece of bread. As you apply it, the honey closest to the bread doesn’t move as quickly as the honey further away; it sticks to the bread. This sticking behavior is similar to the no-slip condition in fluids.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Uniform Flow: Velocity remains constant throughout space.
-
Non-Uniform Flow: Fluid properties change with position in the flow.
-
Streamline: Visual representation of the flow direction and velocity.
-
No-Slip Condition: Fluid velocity at a boundary is zero due to viscosity.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A river flowing steadily at a constant depth and width is an example of uniform flow.
-
The velocity of fluid near a solid wall decreases to zero, demonstrating non-uniform flow due to the no-slip condition.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Flow that’s the same, from place to place, is uniform flow, in this case!
📖 Fascinating Stories
-
Imagine a calm river flowing steadily - there’s consistency in each drop, just like in uniform flow!
🧠 Other Memory Gems
-
U for Uniform = Uneven is Not!
🎯 Super Acronyms
N.U. for Non-Uniform
- Noticeable Unchanges in flow!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Uniform Flow
Definition:
A condition where fluid properties do not change with respect to position in the flow.
-
Term: NonUniform Flow
Definition:
A condition where fluid properties vary at different points in the flow field.
-
Term: Streamline
Definition:
A line in fluid flow that is tangent to the velocity vector at every point, representing flow direction.
-
Term: NoSlip Condition
Definition:
The phenomenon where the velocity of a fluid at a solid boundary is zero due to viscosity.