Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Surface Solitary Waves
Unlock Audio Lesson
Today, we will delve into the world of fluid dynamics, specifically focusing on surface solitary waves. Can anyone tell me what these waves represent in hydraulic engineering?
Are they the waves we see on the surface of water, like ripples?
Exactly! These waves maintain their shape and speed across distances. The key formula to remember here is c = √(gy). What do you think each variable represents?
C is the wave speed, g is the acceleration due to gravity, and y is the depth of water.
Perfect! So, it's important to remember that wave speed is influenced by depth but not by amplitude. Can anyone summarize why fluid density is insignificant here?
It's because the effects of density cancel out in the equations!
That's correct! Density doesn't affect wave speed due to the balance of inertial and hydrostatic pressure effects. Before we move on, what's one practical implication of this knowledge?
It helps in designing canal systems, right? Since we want to predict how waves behave.
Exactly! Understanding these dynamics aids in effective hydraulic design.
Equation of Continuity and Momentum
Unlock Audio Lesson
Now, let's move on to the equations of continuity and momentum. Can anyone remind me what the continuity equation states in the context of open channel flow?
It states that mass flow rate must be conserved, right?
Correct! This leads us to apply the flow equations. If we analyze a control volume with depth y, what relationship do we derive?
We derive the mass flow rate m = ρbc… that relates to width, height, and velocity.
Correct again! By applying momentum principles, we can relate forces acting on the cross sections. What do we get by combining these equations?
We can simplify and find wave speed c is equal to √(gy)! That’s where we started!
Exactly! You all are picking this up quickly. Now, could someone explain what role Froude number plays in our discussion?
Froude number helps classify the flow into subcritical or supercritical based on wave speed compared to flow speed.
Great! So remember, understanding these principles allows us to anticipate how water behaves and ensures effective hydraulic designs.
Practical Implications and Problem Solving
Unlock Audio Lesson
Let’s apply what we learned through some practical problems. For instance, if we have a pond of depth 2 meters, what would be the wave speed?
Using c = √(gy), if g is about 9.81 m/s², the wave speed would be around 4.43 m/s.
Excellent! Now, let’s consider a rectangular channel 3 meters wide carrying 10 m³/s of water at a depth of 2 m. How do we classify the flow?
First, we need to calculate the velocity using Q = A * V. Here, A = width * depth, which gives us V = 1.67 m/s.
Correct approach! Now, knowing the wave speed we derived for 2m of depth is approximately 4.43 m/s, what does that say about the flow condition?
Since flow speed is less than wave speed, it's subcritical!
Right! Understanding these dynamics is key as we move deeper into hydraulic engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
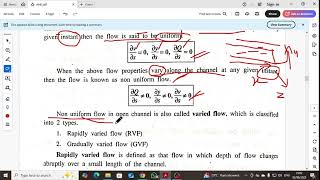
The section provides a detailed analysis of the equations of continuity and momentum as they apply to open channel flow and the results derived for waves in this context. It highlights key formulas for wave speed and discusses the significance of fluid depth and density.
Detailed
Hydraulic Engineering
This section discusses fundamental concepts of hydraulic engineering, specifically focusing on open channel flow and surface solitary waves. The lecture starts with a derivation of key equations using the principles of continuity and momentum. The depth of the fluid (y) and the speed of the wave (c) are considered in this context.
The session details the hydraulic calculations demonstrating how the speed of small amplitude solitary waves is primarily determined by fluid depth with the formula c = √(gy). This highlights that the wave speed does not depend on the wave amplitude, but rather shows a direct relationship to the square root of the fluid depth. Fluid density plays a negligible role in this context, as its effects cancel each other out in the derived equations.
Furthermore, Froude number is introduced, illustrating its significance in determining the nature of the flow as subcritical or supercritical based on the relationship between wave speed and flow speed. The lecture ends with practical problems to reinforce understanding of these concepts.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Waves and Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Welcome back students. In the last lecture we left off by deriving this equation 1, for surface solitary waves and we will continue from this point onwards. So, as we saw if when we applied the equation of continuity to that control volume, we arrived at an equation given by c is equal to y delta V / delta y.
Detailed Explanation
In this section, the professor welcomes students back and refers to their previous lecture where they derived an equation for surface solitary waves. The equation relates the wave speed (c) to the water depth (y) and the change in velocity (delta V) with respect to the change in depth (delta y) using the equation of continuity, which is a fundamental principle in fluid dynamics that states mass flowing in must equal mass flowing out.
Examples & Analogies
Imagine a water slide at a theme park. As the water flows down the slide, it speeds up as the slope increases. Here, the slide represents the control volume in fluid dynamics, and we are analyzing how the flow behaves based on the changing height of the water on the slide.
Application of Momentum Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So now, we proceed further, we have applied equation of continuity now, we should also apply equation of momentum. So, how to apply? So, the mass flow rate m is given by ρbcy, ρ is the density and we need to have volume per unit time. So, b the width, y is the depth and c is the say let us say dx / dt, for example.
Detailed Explanation
Next, the lecturer discusses the application of the momentum equation along with the continuity equation. He explains the mass flow rate (m) as a product of fluid density (ρ), channel width (b), water depth (y), and velocity (c). This establishes a relationship between the physical quantities during analysis, which is crucial for further calculations.
Examples & Analogies
Think of a garden hose. The width of the hose (b) and how much water is flowing (velocity, c) determines how much water comes out (mass flow rate, m). Changing any of these factors, like rolling up the hose (reducing width) or increasing the flow (increasing velocity), impacts the amount of water that exits the hose.
Pressure Forces on the Channel
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, we assume that the pressure is hydrostatic within the fluid and therefore, the pressure force on the channel in cross section 1 will be if you remember from your fluid statics class, it will be ϒy A or gamma where the height was y + delta y.
Detailed Explanation
The professor assumes hydrostatic pressure within the fluid, which dictates how pressure varies with depth. He describes how to calculate the pressure forces on a channel's cross-section, showing the relationship of pressure to water height and area. The equation used incorporates these dimensions to analyze forces acting on a fluid element.
Examples & Analogies
Consider a submerged balloon. The deeper you go in the water, the greater the pressure pushing down on the balloon. The idea is similar to how pressure on the channel increases as the height of water above rises.
Momentum Change and Fluid Dynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, the we apply the change in momentum, we change, rate of change of momentum is the force. So, we obtain half gamma y square b, that is, force on the right-hand side minus force on the left-hand side is equal to rho b c y mass flow rate.
Detailed Explanation
In this section, the focus shifts to applying the momentum change principle in fluid dynamics. The professor explains how to equate the forces from the left and right sides of a control volume and relates this to the mass flow rate. By analyzing momentum change, we derive key relationships that help understand fluid movement in channels.
Examples & Analogies
This can be likened to a crowded subway station: when more people (mass flow) enter (increase in momentum), the force pushing from the crowd needs to balance out with those exiting to ensure the system is stable.
Wave Speed Dependency
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, we just look at this term, and actually if we take half, half common, gamma, gamma common and this b, b common. So, the left hand side I am writing only just trying to, you know, half gamma, b is going to be common, it will be y square - y + delta y whole square.
Detailed Explanation
The discussion continues on simplifying the equations derived from previous calculations by factoring out common terms. This step is essential for realizing how changes in one variable affect the overall wave speed calculation in the channel, ultimately leading to the specific equations governing wave behavior.
Examples & Analogies
Consider a team of workers trying to pull a cart. If they coordinate pulling together (taking common factors), it is far more efficient than if they were pulling on different sides (discrepancy in wave speed calculations).
Final Equation for Wave Speed
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, we have now this equation number 2. So, what are we going to do? So, we are going to equate equation 2 into equation 1. If you go back and see what the equation 1 was, equation 1 was c is equal to y delta V / delta y.
Detailed Explanation
The culmination of the preceding discussions leads to the formulation of an essential equation for wave speed. By equating previously derived equations, the students arrive at the conclusion that wave speed (c) is proportional to both the acceleration due to gravity and the depth of water, demonstrating the principles of wave motion in open channels.
Examples & Analogies
Imagine riding a wave in the ocean. The deeper you are (higher water depth) and the stronger the wave is (gravity) determine how fast you glide forward; this equation encapsulates that relationship.
Concept of Froude Number
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, there is a Froude number effect also in solitary waves. Froude number as we discussed is given by V under root g y. This is the definition.
Detailed Explanation
In this chunk, the concept of the Froude number is introduced as a dimensionless number that compares the flow velocity to wave speed. This is a crucial concept in identifying the type of flow (subcritical or supercritical) within channels and predicting how waves behave under different conditions.
Examples & Analogies
Think of crossing a river. If you are swimming against the current (velocity) and facing waves from boats nearby (wave speed), the Froude number helps you understand if you will be pushed back (supercritical flow) or if you could swim upstream (subcritical flow).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Surface Solitary Waves: These are waves that maintain their shape while traveling across a fluid’s surface.
-
Continuity and Momentum Equations: Principles that govern the conservation of mass and momentum in fluids.
-
Froude Number: A measure of the flow regime, indicating whether it is subcritical or supercritical.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A wave traveling across a pond at a depth of 2 meters with a speed of 4.43 m/s is an example of calculating wave parameters.
-
In a rectangular channel carrying water at a certain depth, the flow can be classified as subcritical or supercritical based on velocity compared to wave speed.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To find wave speed, just remember this, depth and gravity, can't miss.
📖 Fascinating Stories
-
Imagine a small pond where waves dance gracefully, governed by depth and gravity, unaffected by the breeze.
🧠 Other Memory Gems
-
Remember C for Condition: wave speed depends on depth, not the fluid's weight.
🎯 Super Acronyms
WAVE
- Wavelength and Amplitude determine Velocity Effectively.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Surface Solitary Waves
Definition:
Waves that maintain their shape while traveling at a constant speed across a surface.
-
Term: Continuity Equation
Definition:
An equation that expresses the principle of conservation of mass in fluid dynamics.
-
Term: Momentum Equation
Definition:
An equation that relates the forces acting on fluid elements to the changes in momentum.
-
Term: Froude Number
Definition:
A dimensionless number used to determine flow regimes; Froude number < 1 indicates subcritical flow, while > 1 indicates supercritical flow.
-
Term: Hydrostatic Pressure
Definition:
Pressure exerted by a fluid at equilibrium due to the weight of the fluid above it.
-
Term: Wave Speed (c)
Definition:
The speed at which a surface solitary wave travels in the fluid, influenced by fluid depth.