Hydraulic Engineering
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Trapezoidal Channel Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will analyze a trapezoidal channel. We have a bottom width of 10 meters, a side slope ratio of 1.5, and a Manning's n value of 0.015. Can someone tell me what we need to find in this scenario?

We need to find the bottom slope necessary to pass 100 cubic meters per second at a depth of 3 meters.

Exactly! To start, we will calculate the area of the channel. Can anyone recall the formula for area?

The area can be calculated as base times height plus the area of the triangular section.

Correct! The area comes out to 43.5 square meters. Now, let’s find the wetted perimeter using the formula. Any guesses on how to approach this?

We can use the bottom width plus the length of the slopes to compute the perimeter.

Right again! The hydraulic radius is determined by dividing the area by the perimeter. Remember, hydraulic radius R is A/P. Now let's calculate Q using Manning's equation.

So we'll plug the values into Q = (1/n)AR^(2/3)S0^(1/2)?

Exactly! And solving it gives us S0. Always remember to check your units! Let's summarize what we covered today.
Circular Channel Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Moving on to circular channels, let's consider a pipe with a diameter of 0.80 meters carrying a flow at a depth of 0.30 meters on a slope of 1 in 900. What's the first step in solving this?

We need to calculate the area of the flow section, right?

Yes! We will find it using the angle theta. Who can remember how to find this area?

It's the area of the sector minus the triangle area!

Correct! Using the sector formula, we can derive the area as 0.1722 square meters. Now, what about the wetted perimeter?

It is half the diameter multiplied by the angle in radians.

Exactly! After calculating the wetted perimeter and hydraulic radius, we will use Manning's formula again to estimate discharge. Any questions on the calculations?

Can we use the same method for different shapes?

Absolutely! Each channel shape will have its specific formulas, but the principles remain similar. Let’s wrap up this session by calculating the discharge.
Best Hydraulic Cross Section
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s explore what we refer to as the best hydraulic cross section. Can anyone describe what that is?

I believe it’s the section that minimizes area while maximizing flow for given conditions.

Exactly! For optimal flow, we want to minimize the cross-sectional area for a specified discharge. How would we express the depth of flow that maximizes velocity?

I think we derive expressions based on the area and perimeter.

That's right again! We can work through these calculations together using theta and displacement equations. It’s key for understanding channel efficiency!

Can this apply to different slopes or materials?

Certainly! Best hydraulic conditions apply broadly, but each design needs consideration for flow characteristics. Let's summarize the key takeaway of maximizing flow efficiency.
Hydraulic Radius and Manning's Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s delve deeper into relationship that hydraulic radius has with different flow shapes. Who remembers the formula?

It’s area divided by the wetted perimeter!

Exactly! And why is this important?

Because it helps determine flow rate and efficiency of the channel shape!

Fantastic! Applications of Manning's equation help us design channels that lead to specific performance standards. What do you think the real-world implications are?

It affects drainage, irrigation, and even flood control efforts?

Precisely! Knowing the hydraulic radius and applying Manning’s Equation aids in effective infrastructure design. Let’s summarize this critical understanding.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section delves into various hydraulic engineering problems, specifically focusing on open channel flow and uniform flow. Key discussions include the calculation of depth, discharge, and hydraulic radius in different channel shapes while utilizing Manning's formula.
Detailed
Hydraulic Engineering: Introduction to Open Channel Flow and Uniform Flow
This section explores fundamental principles of hydraulic engineering, particularly the analysis of open channel flows and the application of Manning's equation for calculating flow characteristics in various channel shapes. It begins with examples of trapezoidal and circular channels where the depth of flow, hydraulic radius, and discharge are calculated using known parameters such as channel slope and roughness coefficient. The importance of the best hydraulic cross-section is introduced, detailing how to derive expressions that maximize flow efficiency in circular and triangular channels. Students engage with equations and conceptual problems that clarify the conditions for maximum discharge while reinforcing the application of mathematical principles to real-world hydraulic scenarios.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Lecture
Chapter 1 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Welcome back. So, last lecture at the end of last week, we saw that the normal depth. We found out in this particular question was 1.5 meter. Although the problem in itself was very simple and easy, but the calculation was very complex, but I hope this has given you a good idea. Now, we are going to solve another question, at the beginning of this lecture itself.
Detailed Explanation
In this introductory section, the professor is welcoming students back and reflecting on the previous lecture's focus on normal depth calculations. He highlights the complexity of the calculations despite the simplicity of the problem, setting the stage for a new problem-solving session.
Examples & Analogies
Think of a cooking recipe that seems easy and straightforward, but requires precise measurements and techniques, making it more complicated. Similarly, hydraulic engineering problems may seem simple on the surface but can have intricate calculations involved.
First Problem: Trapezoidal Channel
Chapter 2 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A trapezoidal channel has a bottom width of 10 meter and a side slope of 1.5 horizontal is to 1 vertical. The Manning's n is also given as 0.015. Now, the question is, what bottom slope is necessary to pass 100 meter cube per second of discharge in this channel at a depth of 3 meter.
Detailed Explanation
Here, the problem involves a trapezoidal channel characterized by specific geometric parameters - a bottom width of 10 meters and a side slope of 1.5:1. The Manning’s roughness coefficient (n=0.015) is provided, and students need to determine the slope required to allow a discharge of 100 cubic meters per second at a depth of 3 meters. The problem links geometry and hydraulics to find the necessary channel slope.
Examples & Analogies
Imagine designing a water slide; you need to find the right angle or slope to ensure water flows down smoothly. Similarly, in hydraulic engineering, finding the correct slope is crucial to managing water flow efficiently.
Calculating Area and Wetted Parameter
Chapter 3 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This is 10, this is 3, this is 4.5, so area is 10 into 3 plus half, base is 4.5 into 3, for this one, and plus same is for this one, into 2. So, area is going to be 43.5 meters square.
Detailed Explanation
In this part, the professor demonstrates how to calculate the area of the trapezoidal channel using its geometric properties. He describes taking the bottom width and side slopes to determine the area mathematically. This helps students understand how physical dimensions translate into hydraulic calculations.
Examples & Analogies
Consider filling a rectangular swimming pool; you need to know the dimensions to calculate the volume of water needed. In our trapezoidal channel, we're doing something similar—calculating the area to understand how much water it can hold.
Finding Hydraulic Radius
Chapter 4 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Therefore, hydraulic radius is A / P, so 43.5 / 20 that is 2.09 meter. So, we have been able to find out area, we have been able to find out perimeter, we have been able to find out the hydraulic radius.
Detailed Explanation
The hydraulic radius is defined as the ratio of the area of flow (A) to the wetted perimeter (P). In this example, after calculating the area, the professor calculates the wetted parameter, leading to the determination of the hydraulic radius, which is an essential factor in flow calculations in open channel hydraulics.
Examples & Analogies
Just like calculating the width and depth of a garden bed to determine how much soil is needed, in hydraulic engineering, we calculate the hydraulic radius to determine flow characteristics for designing channels.
Using Manning's Formula
Chapter 5 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
By Manning's formula, Q is 1 / n AR to the power 2 / 3 S 0 to the power half.
Detailed Explanation
Manning’s formula relates the discharge (Q) of water flowing through the channel to the area (A), hydraulic radius (R), slope (S0), and Manning’s n coefficient, which reflects channel roughness. This formula is fundamental in hydraulic engineering for calculating how water behaves in open channels.
Examples & Analogies
Think of driving a car on different road types—smooth asphalt (low roughness) vs. a dirt road (high roughness). The friction changes how fast you can drive, similar to how roughness in a channel affects water flow.
Calculating Channel Slope
Chapter 6 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, this comes out to be 100 is equal to 4740 into S 0 to the power half, and if you calculate, S 0 will come out to be 4.451 into 10 to the power minus 4.
Detailed Explanation
In this step, the professor rearranges Manning's formula to solve for the slope (S0). After substituting determined values into the formula, he calculates the necessary channel slope to achieve the desired discharge. This application illustrates the connection between mathematical principles and practical engineering requirements.
Examples & Analogies
Consider how adjusting the angle of a ramp changes the speed of a rolling ball; in engineering, changing the slope can alter how quickly water flows, making this calculation crucial for managing water flow effectively.
Next Problem: Circular Drainage Pipe
Chapter 7 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, a circular drainage pipe of 0.80 meter in diameter conveys discharge at a depth of 0.30 meter...
Detailed Explanation
The second problem transitions from trapezoidal channels to circular drainage pipes, showcasing the versatility of hydraulic engineering. Students must adapt their calculations to the new geometry, emphasizing the importance of understanding different channel shapes in hydraulics.
Examples & Analogies
Transitioning from trapezoidal to circular structures in engineering is similar to switching from square to round cake pans—while the concept remains the same, the measurements and calculations differ, highlighting the need for adaptability.
Calculating Area of Circular Flow Section
Chapter 8 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This sector, you know, area of the sector O M N is very simple, half r square into 2 theta.
Detailed Explanation
In this section, the professor discusses calculating the area of the flow section within the circular pipe. He elaborates on using geometric principles to determine the area of the sector formed by the water's surface and the triangle created by the water level in the pipe. Understanding this involves both area calculations and spatial visualization.
Examples & Analogies
Picture a slice of pizza; the area of the pizza slice (sector) must be calculated to know how much cheese and toppings to add. Similarly, calculating the flow area of a circular pipe determines how much water can flow through it.
Finding Wetted Perimeter in Circular Pipe
Chapter 9 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, as I said, area of the sector O M N minus area of the triangle O M N.
Detailed Explanation
Here, the wetted perimeter is derived by subtracting the area of the triangular section from that of the circular sector to find the wetted area in the pipe. This calculation is important for understanding how much of the pipe's surface is in contact with flowing water, affecting flow behavior.
Examples & Analogies
Think about how much of your hand is wet after washing; the area in contact with water matters, similar to how engineers need to know the wetted perimeter to analyze water flow in pipes effectively.
Conclusion and Upcoming Topics
Chapter 10 of 10
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, this is enough for today's first lecture of this week, from next lecture onward. For this week, we will be dealing with gradually varied flow.
Detailed Explanation
In the conclusion of this lecture, the professor summarizes the learned concepts and provides a preview of future topics, gradually varying flow. This closing helps students anticipate upcoming lectures and fosters continuity in their learning.
Examples & Analogies
It’s similar to finishing a chapter in a book—after summarizing what you learned, you look forward to the next, laying the groundwork for future knowledge.
Key Concepts
-
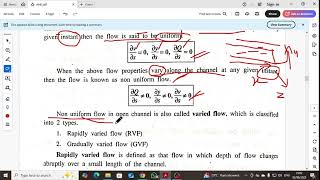
Open Channel Flow: Flow of liquid in a channel that is open to the atmosphere.
-
Manning's Formula: An important equation used to estimate the flow rate in open channels.
-
Trapezoidal and Circular Channels: Two common channel shapes analyzed in hydraulic engineering.
Examples & Applications
A trapezoidal channel with a bottom width of 10 meters carrying a discharge of 100 m³/s can be analyzed with Manning's equation to find the necessary channel slope.
In a circular channel of 0.80m diameter at a depth of 0.30m, the flow characteristics can be determined by calculating flow area and wetted perimeter.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In a channel wide and deep, flow is what we want to keep. Use Manning's rule with care, to find discharge and beware!
Stories
Imagine a flowing river navigating through valleys; it seeks the path of least resistance, much like engineers seeking efficient designs using hydraulic principles.
Memory Tools
Remember 'A-P-R' for Area, Perimeter, and Radius when calculating flow!
Acronyms
R.A.P
Radius is Area divided by Perimeter.
Flash Cards
Glossary
- Hydraulic Radius
The ratio of the area of flow to the wetted perimeter in a channel.
- Manning's Equation
An empirical formula that relates the flow rate in open channels to the channel characteristics and roughness coefficient.
- Wetted Perimeter
The length of the line of contact between the water and the channel walls.
- Discharge (Q)
The volume of fluid flowing through a given cross-section per unit time.
- Best Hydraulic Cross Section
The channel configuration that minimizes the flow area for a given discharge and slope.
Reference links
Supplementary resources to enhance your learning experience.
