Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Large Eddy Simulation
Unlock Audio Lesson
Today we are discussing Large Eddy Simulation, or LES. It serves as a middle ground between Direct Numerical Simulation, which is highly accurate but demands substantial computational resources, and Reynolds-Averaged Navier-Stokes, which employs simplifications at the cost of accuracy. Can anyone tell me why we might need LES?
I think it's because we want to balance accuracy and computational time!
Exactly! By focusing on larger eddies and modeling smaller ones, we can manage computational resources efficiently. This brings us to the next question: what are large and small eddies based on their behavior?
Are large eddies anisotropic and more affected by the flow geometry?
Correct! Large eddies are indeed anisotropic, while smaller eddies behave isotropically. Let’s remember that anisotropic can be abbreviated as 'A' for 'Angled behavior'.
Understanding the Eddies
Unlock Audio Lesson
Now, let’s delve deeper into how these eddies interact. Large eddies extract energy from the mean flow. What do you think smaller eddies do?
They take energy from larger eddies, right?
Exactly! This shows us the energy cascade concept, where energy moves from large to small scales. We can call this the 'Cascade of Energy', an important principle in turbulence. Can anyone recall Kolmogorov’s theory regarding this?
Isn’t it that only the smaller scales have a universal behavior while large scales vary?
Great recall! It highlights why modeling smaller eddies is more straightforward. Now, let's summarize this session. We learned that large eddies extract energy, and smaller ones pass it on, illustrating the cascade phenomenon.
Filtering in LES
Unlock Audio Lesson
Next, let’s discuss the filtering process used in LES. The grid plays a crucial role in distinguishing between large and small eddies. Who can explain what is meant by 'filter width' in this context?
Is it related to how we decide the size of the grid cells?
Precisely! The filter width should be approximated to the size of the mesh to effectively capture the relevant scales. We say that the mesh should be smaller than the eddies it aims to capture. What terms do we use for these different scale issues?
We have grid scales for large eddies and sub-grid scales for smaller ones!
Correct! And understanding these terms is essential for effective modeling in LES. To summarize, we discussed how the filtering operation helps us focus on significant eddies, while the grid size is key to that process.
Governing Equations and Terms
Unlock Audio Lesson
Finally, let’s wrap up with the governing equations of LES. The filtered momentum equation is crucial here. Who remembers what the term tau ij represents?
Isn’t it related to sub-grid scale stress?
Exactly! Tau ij accounts for the effects of the smaller eddies on the larger ones, and remember it consists of the Leonard terms and Reynolds stresses. This equation helps in better turbulence modeling.
Does this mean that we only focus on larger turbulent structures in our calculations?
Yes. By modeling larger eddies directly, while approximating the smaller ones, we optimize computational efficiency without sacrificing too much accuracy. Let’s summarize: we covered the filtered momentum equation and the significance of controlling both the large and small scales in simulations.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Large Eddy Simulation (LES) is a technique used in computational fluid dynamics to analyze turbulent flows by capturing the behavior of large-scale eddies, which dominate the flow dynamics, while modeling the smaller eddies. This approach strikes a balance between accuracy and computational resource demands compared to Direct Numerical Simulation (DNS) and Reynolds-Averaged Navier-Stokes (RANS) methods.
Detailed
Large Eddy Simulation (LES) is a vital approach in computational fluid dynamics that overcomes the limitations of both Direct Numerical Simulation (DNS) and Reynolds-Averaged Navier-Stokes (RANS) methods. While DNS provides high accuracy at the cost of substantial computational time, RANS relies on simplifications that can compromise accuracy. LES captures the dynamics of large turbulent eddies, which are more influenced by geometry and boundary conditions, while small eddies are modeled using turbulence models. The essence of LES lies in the filtering process that separates large and small scales, governed by the grid size designed for capturing large eddies. The governing equations used in LES incorporate filtered momentum equations and various terms, including sub-grid scale stresses. Understanding these dynamics offers significant insights into turbulence modeling and the quest for universal turbulence models, particularly the Kolmogorov hypothesis concerning energy cascades in turbulent flows.
Youtube Videos
![[CFD] Large Eddy Simulation (LES): An Introduction](https://img.youtube.com/vi/r5vP45_6fB4/mqdefault.jpg)
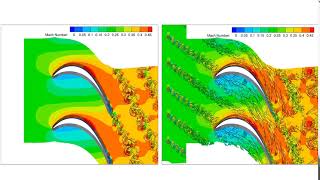
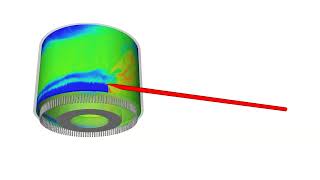
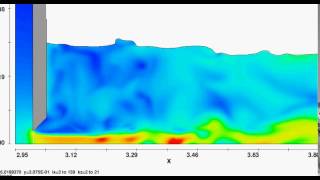
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Large Eddy Simulation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Another such technique is called Large Eddy simulation. See in the DNS one important thing to note was that we had the best accuracy but a lot of computational time is required. LES is a sort of a tradeoff between the Reynolds average; in Reynolds average we do many approximations so the results are not that accurate compared to DNS, but LES is something which is a tradeoff between DNS and Reynolds average Navier Stokes equation.
Detailed Explanation
Large Eddy Simulation (LES) is a computational fluid dynamics (CFD) technique that represents a middle ground between Direct Numerical Simulation (DNS) and Reynolds Averaged Navier-Stokes (RANS) methods. LES aims to achieve a balance between accuracy and computational feasibility. While DNS offers the highest accuracy, it requires substantial computational resources. On the other hand, RANS involves numerous approximations that can compromise result accuracy. LES maintains more effective accuracy than RANS by resolving large turbulent structures (eddies) directly and modeling the effects of small turbulent structures.
Examples & Analogies
Think of LES as a detailed map of a mountain range. DNS is like a satellite image that captures every tiny detail of the landscape, which requires a lot of processing power to store and interpret. RANS, however, is more like a rough sketch, where many details are simplified or omitted for ease of understanding. LES, on the other hand, provides a comprehensive view of the mountain range, capturing the prominent peaks while using simplified representations of the valleys, making it manageable while still insightful.
Behavior of Eddies in Turbulent Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
There is a big difference in the behaviors of large and small eddies in turbulent flow fields. Large eddies are more anisotropic, and their behavior is dictated by the geometry of the problem domain. In contrast, small eddies are nearly isotropic and have a more universal behavior, as described by Kolmogorov.
Detailed Explanation
In turbulent flows, the interaction and behavior of eddies (swirling motions in the fluid) vary significantly based on their size. Large eddies tend to be influenced by the overall geometry and conditions of the environment, rendering them anisotropic, meaning their characteristics change based on direction. Small eddies, however, exhibit nearly isotropic behavior; they are similar from all angles. Kolmogorov’s theory explains that these smaller eddies behave uniformly across various conditions, making them easier to model in simulations.
Examples & Analogies
Imagine a large windstorm creating enormous swirling clouds (large eddies) influenced by the shape of the land below. These clouds might behave differently around mountains or cities. Now, think about dust motes swirling in the air (small eddies); they seem to twirl around in all directions regardless of the landscape beneath, demonstrating a uniform pattern of behavior.
Energy Transfer in Eddies
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Large eddies extract energy from the mean flow, while small eddies take energy from slightly larger eddies. This energy transfer occurs in a cascading manner, referred to as the Kolmogorov hypothesis, which highlights a major challenge in developing universal turbulence models.
Detailed Explanation
In the world of turbulent flows, energy transfer takes place in a hierarchical cascade. Larger eddies draw energy from the primary flow, while smaller eddies 'feed' off energy flows from the larger ones. The Kolmogorov hypothesis posits that this energy transfer hierarchy is universal in turbulent systems, creating complexity when developing comprehensive turbulence models. The vast differences in behavior between large and small eddies create challenges for researchers in formulating a single model to accurately describe turbulence across all scales.
Examples & Analogies
Think of a large river (mean flow) that feeds into a series of interconnected ponds. The larger ponds represent big eddies, soaking up water (energy) from the river, while smaller pools nearby represent the small eddies, gaining water from the larger ponds. The process of water flowing from one body to the next resembles the cascading energy transfer in turbulent flows.
Implementation of LES
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In LES, the larger eddies are computed with a time-dependent simulation where the influence of the small eddies is incorporated through a turbulence model. The grid size is set to capture the largest eddies with spatial filtering operation to separate the large and small eddies.
Detailed Explanation
LES employs a unique approach where the larger turbulent motion (eddies) is directly calculated over time, while the effects of smaller eddies are quantified using turbulence models. This is achieved by strategically sizing the computational grid so that it can effectively capture the largest eddies. A filtering process is used to differentiate between large and small eddies, ensuring that the simulation remains manageable while accurately modeling the dynamics of the flow.
Examples & Analogies
Consider a photographer trying to capture a scene with both a wide-angle and close-up view. The wide-angle lens represents the large eddies, capturing the overall landscape, while the close-up lens signifies small eddies, focusing on intricate details. The photographer must choose their lens wisely to provide a balanced representation without losing critical information about the larger scene.
Grid and Filtering in LES
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The filtering operation is defined by a filter function, and the filter width is set to be close to the size of the mesh. The grid scales are for large eddies, while subgrid scales account for the smaller eddies.
Detailed Explanation
The filtering operation in LES serves to distinguish between the effects of large and small eddies based on their scales. The grid size is crucial as it must effectively encompass the dimensions of the larger eddies, allowing them to be computed accurately. For smaller eddies, which cannot be captured directly due to their size, a model is applied to estimate their impact on the flow dynamics through subgrid scaling.
Examples & Analogies
Imagine sifting flour when baking. The large pieces remain in the sifter (large eddies), while the fine powder passes through (small eddies). The sifter represents the mesh size in the simulation. Using a modeling technique to estimate the behavior of the finer particles allows the baker to ensure the final mixture remains smooth and consistent without capturing every single speck of flour.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Large Eddy Simulation (LES): A technique focusing on large turbulent structures while modeling small ones.
-
Energy Cascade: The transfer of energy from large eddies to smaller ones, a fundamental aspect of turbulent flows.
-
Anisotropic vs. Isotropic Eddies: Large eddies exhibit anisotropic behavior while small eddies behave isotropically.
-
Subgrid Scale (SGS): Scales smaller than the grid scale, modeled rather than resolved in LES.
-
Filtered Momentum Equation: The primary equation in LES that captures the effects of turbulence.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of LES application is in predicting weather patterns, where capturing large-scale atmospheric movements is essential.
-
In aerospace engineering, LES is used to simulate the turbulence around aircraft wings for better aerodynamic design.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Big waves can roar, they take the floor; Small ones swirl, they spin and twirl - that's the flow!
📖 Fascinating Stories
-
Imagine a river where big fish chase smaller fish. The big fish represent large eddies, hunting for energy from the current while the small ones scurry in between.
🧠 Other Memory Gems
-
Remember L.E.S for Large Eddy Simulation, where E means Energy extraction and S means Smaller eddies modeled!
🎯 Super Acronyms
LES
- Large energy
- small modeling - focuses on large turbs and smooths the rest.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Large Eddy Simulation (LES)
Definition:
A turbulence modeling technique that resolves large-scale turbulent eddies while using models for the smaller scales.
-
Term: Direct Numerical Simulation (DNS)
Definition:
A computational method that solves the Navier-Stokes equations without any turbulence models, focusing on the complete flow field.
-
Term: ReynoldsAveraged NavierStokes (RANS)
Definition:
A simplified approach to turbulence modeling that averages the effects of turbulent fluctuations.
-
Term: Eddies
Definition:
Circular currents in a fluid that exhibit turbulence, classified into large and small based on their size and behavior.
-
Term: Kolmogorov Hypothesis
Definition:
A theory suggesting that smaller eddies have universal behavior compared to larger eddies, crucial for turbulence modeling.
-
Term: Filtering
Definition:
A process in LES that separates large-scale from small-scale turbulent structures based on grid size.
-
Term: Grid Scale (GS)
Definition:
The scales directly resolved in the computational grid representing large eddies.
-
Term: Subgrid Scale (SGS)
Definition:
The smaller scales that are not directly resolved by the grid but influenced by turbulence models.
-
Term: Filtered Momentum Equation
Definition:
The governing equation in LES accounting for the influence of both large and small eddies.
-
Term: Energy Cascade
Definition:
The process by which energy transfers from larger turbulent structures to smaller ones.