Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Regime Channels
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're covering regime channels. These are channels that flow under constant discharge and maintain a stable state over time. Can anyone tell me why stability is important?
Stability in channels helps prevent flooding and ensures consistent irrigation.
Exactly! If a channel remains stable, there's no significant erosion or deposition. This is vital for both irrigation and flood control. Now, can someone explain what we mean by a 'true regime'?
True regime is the final equilibrium state where the channel has adapted to its flow conditions.
Good job! There are three stages leading to this final state: initial regime, quasi regime, and true regime. Remember this sequence—think of it as I-Q-T, Initial, Quasi, True.
Kennedy’s Theory
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let’s dive into Kennedy’s theory. Who remembers the year he developed his theory?
He developed it in 1895!
Exactly! Kennedy's theory relies on the critical velocity to maintain a non-silting channel. What’s critical velocity again?
It’s the minimum velocity required to prevent silting!
Correct! The equation he provided is Vc = 0.55·D^0.64. How does depth affect critical velocity?
Deeper flows require less velocity to maintain stability.
Right! Remember this equation; it's key for understanding channel design.
Lacey’s Theory
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next up is Lacey’s theory, which builds on Kennedy’s ideas. What makes Lacey’s theory unique?
Lacey studied a wider range of systems, not just one canal!
Excellent observation! Lacey’s approach gives us empirical equations that describe regime conditions. Can anyone recall his velocity equation?
Yes! It’s V = k·f^1/2·R^2/3!
Spot on! Lacey’s formulas allow for better predictions of channel behavior. So, when designing a channel, which theory would be preferable?
Lacey’s would be better since it accounts for various systems!
Right again! Lacey’s theory is much more comprehensive.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Kennedy’s theory, developed in 1895, focuses on the critical velocity required to prevent silting in channels while Lacey’s theory, created in 1930, refines this with broader empirical studies and includes additional design equations. Both theories are essential for understanding and designing stable irrigation and drainage channels.
Detailed
Kennedy’s and Lacey’s Theory of Regime Channels
The study of regime channels in water resources engineering aims to design channels that maintain a stable state over time, balancing sediment transport without significant erosion or deposition. Two foundational theories, Kennedy’s (1895) and Lacey’s (1930), provide frameworks for understanding these dynamics. Kennedy’s theory introduces the concept of critical velocity, necessary for preventing silting in channels based on specific characteristics and empirical observations from the Upper Bari Doab Canal System. Meanwhile, Lacey’s theory expands upon Kennedy's ideas, presenting empirical equations that account for various canal systems and sediment factors, thereby solidifying its application in channel design. The section comprehensively explores both theories, their assumptions, critical equations, limitations, and relevance in modern practices of water resources management.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Regime Channels
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Designing stable channels for irrigation, drainage, and flood control is a key aspect of water resources engineering. Channels that neither silt up nor scour are termed regime channels. The development of regime theories has played a vital role in understanding how natural and artificial channels adjust themselves over time to reach a state of equilibrium. Two major theories have historically contributed to this understanding:
• Kennedy’s Theory (1895) – Based on empirical studies of the Upper Bari Doab Canal System in Punjab.
• Lacey’s Theory (1930) – A more refined theory based on observations from a wide range of canal systems. This chapter presents both theories in detail, exploring their assumptions, derivations, limitations, and applications.
Detailed Explanation
This introduction explains the importance of designing stable channels for managing water resources effectively. Regime channels are special types of channels that maintain a balance between sediment deposition and erosion, resulting in stable characteristics over time. The text introduces two foundational theories by Kennedy and Lacey, which help engineers understand how these channels function and adjust over time.
Examples & Analogies
Think of a river as a highway for water. Just like a well-planned highway has lanes that allow cars to move smoothly without getting stuck in traffic or veering off-course, a regime channel is designed to flow smoothly without accumulating too much sediment or eroding its banks.
Concept of Regime Channels
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
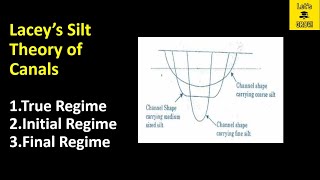
A regime channel is a channel flowing under constant discharge and carrying sediment load in such a way that over time, its cross-sectional shape, bed slope, and other characteristics adjust to achieve a stable state. In this state, there is no significant erosion (scouring) or deposition (silting). These channels form naturally or gradually adjust if constructed under suitable conditions. Three types of regime stages are commonly defined:
1. Initial Regime – Immediate response after the canal is put into use.
2. Quasi Regime – Intermediate stage, where some stability exists.
3. True Regime – Final equilibrium state, achieved over time with stable discharge and sediment load.
Detailed Explanation
The text defines what a regime channel is and describes its features. A regime channel maintains a consistent flow and sediment load, which helps it evolve into a stable structure over time. It describes three important stages these channels go through: the initial response as the channel is first used, a quasi-regime that indicates some level of stability, and the true regime where the channel has fully stabilized.
Examples & Analogies
Imagine a garden hose. Initially, when you first turn on the water, it may bend and spill some water. As you hold it straight, it stabilizes, allowing the water to flow smoothly without any leaks—the initial phase is like the hose's early days of use, the quasi regime is when it starts to stay in place, and the true regime is when the water flows perfectly without problems.
Kennedy’s Theory of Regime Channels
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
47.2.1 Historical Background: R.G. Kennedy developed his theory in 1895 based on observations of stable channels in the Upper Bari Doab Canal system in British India. He attempted to find a relationship between channel dimensions and flow characteristics in alluvial soils.
47.2.2 Key Assumptions:
1. The channel carries silt-laden water in suspension.
2. There is no scouring or silting in the channel.
3. The bed slope and cross-section adjust to produce critical velocity, which prevents deposition or erosion.
4. The critical velocity depends on the depth of flow.
Detailed Explanation
This section discusses Kennedy's work and the foundational assumptions of his theory. Kennedy's empirical observations led him to propose key assumptions about stability in channel flow, including the behavior of silt, the conditions under which erosion and sedimentation can be prevented, and how channel dimensions relate to flow.
Examples & Analogies
Consider Kennedy's theory like a chef figuring out the right mix of ingredients for a cake. If you get the proportions just right (depth of flow leads to the right velocity), the cake (or channel) holds together without falling apart (eroding or silting).
Critical Velocity Concept in Kennedy’s Theory
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Kennedy introduced the concept of critical velocity (Vc) — the minimum velocity required to prevent silting in the channel. He gave the empirical relation: V = 0.55·D^0.64, where V is critical velocity (m/s) and D is depth of flow (m). He later included a critical velocity ratio (m) to adjust for sediment properties: Vc = m·0.55·D^0.64. Here, m>1 indicates coarser sediments, requiring higher velocity to avoid silting, while m<1 represents finer sediments.
Detailed Explanation
This chunk focuses on the critical velocity concept that Kennedy developed. He identified a specific velocity that must be maintained to ensure sediment doesn't settle in the channel, leading to clogging. The formula he provided allows for adjustments based on sediment type, making the theory versatile but still bound by limitations.
Examples & Analogies
Think of it like a river trying to keep its flow constant. If the flow is too slow (below critical velocity), sand and dirt will settle like sediment in a shaken bottle. Maintaining the right speed prevents this build-up, ensuring the river keeps flowing smoothly.
Limitations of Kennedy’s Theory
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Based only on one canal system.
• Lacks general applicability to various sediment sizes and discharges.
• Does not provide a method to compute slope directly.
• Does not consider bed width explicitly in velocity expression.
Detailed Explanation
Kennedy's theory, while innovative for its time, has notable limitations. It was developed from a single canal system, which may not accurately represent varying conditions elsewhere. Additionally, the theory is not as effective for different sediment types, and it doesn't provide a clear way to calculate certain important factors like channel slope or bed width, which are crucial for practical applications.
Examples & Analogies
You can think of it like a recipe that only works for one specific oven. If you try using it in another oven or with different ingredients (like different sediment types), it might not give the desired results—meaning Kennedy’s theory works well in specific instances but may not be broadly applicable.
Lacey’s Theory of Regime Channels
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
47.3.1 Background and Development: Lacey expanded upon Kennedy’s ideas, conducting broader field studies on various canals in alluvial soils. His theory is more comprehensive and widely used for the design of stable channels.
47.3.2 Basic Assumptions:
1. Channel is in regime (true equilibrium).
2. The sediment load and size are constant over time.
3. Uniform discharge flows constantly.
4. Channel cross-section is approximately semi-elliptical.
5. The channel material is the same as that being transported.
Detailed Explanation
This part introduces Lacey’s theory, which builds upon Kennedy's foundation and seeks to provide a more universal understanding of channel behavior. Lacey's assumptions cover broader conditions, such as assuming a stable equilibrium of sediment load and flow, thus allowing for more practical applications in design and engineering.
Examples & Analogies
Imagine Lacey's theory like a more advanced guidebook for travelers. While Kennedy had a narrow focus on one city (or canal), Lacey wrote a comprehensive guide covering multiple regions (canal types and alluvial soils), providing better insight into how to navigate different conditions successfully.
Lacey’s Regime Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Lacey developed four empirical equations to describe regime conditions:
(a) Velocity Equation: V = k · f1/2 · R2/3, where V = velocity (m/s), f = silt factor, R = hydraulic radius (m), k = 1. Later simplified to: V = 0.48 · f1/2 · R2/3.
(b) Discharge Equation: Q = A · V. Combined with the velocity equation, Lacey derived: Q = 2.5 · V5/f2.
(c) Wetted Perimeter (P): P = 4.75 · Q.
(d) Regime Slope (S): S = Q1/3 or alternatively: S = V5/140 · Q.
(e) Silt Factor (f): f = √(1.76 · d), where d is the mean sediment size in mm.
Detailed Explanation
This chunk outlines the empirical equations that Lacey put forward to describe various aspects of regime channels. The equations cover critical elements such as velocity, discharge, wetted perimeter, slope, and the silt factor, providing engineers with the necessary mathematical relationships to design efficient and stable channels.
Examples & Analogies
Think of Lacey's equations as formulas for different aspects of a car's performance, like speed, fuel efficiency, and tire traction. Each equation is crucial for understanding how to optimize car performance, just like these regime equations help optimize canal design.
Design Procedure using Lacey’s Theory
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Determine discharge Q and sediment size d.
- Compute silt factor f using f = 1.76 · d.
- Assume initial velocity or compute from: (Q · f2)^(1/5).
- Find area A from A = Q/V.
- Determine wetted perimeter P = 4.75 · Q.
- Calculate hydraulic radius R = A/P.
- Estimate slope S using: S = V5/140 · Q.
Detailed Explanation
This section provides a step-by-step design procedure that engineers can follow when using Lacey’s theory. It lays out a clear method starting from determining the flow and sediment characteristics and progressively working through to calculating necessary parameters for stable channel design.
Examples & Analogies
Imagine setting up a new aquarium. First, you need to know how much water (discharge) you need and the size of the fish (sediment). Then, you measure the aquarium dimensions (area) and figure out how much filtration (slope) and water circulation (velocity) is needed to keep everything stable and healthy.
Limitations of Lacey’s Theory
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Based on empirical data – may not hold outside Indian alluvial regions.
• Does not explicitly handle non-uniform sediment loads.
• Assumes semi-elliptical sections; actual channels may vary.
• Does not consider bank erosion or vegetative resistance.
Detailed Explanation
Like Kennedy’s theory, Lacey's theory also has limitations. Its basis on specific empirical data raises concerns about its applicability in different geographic areas or conditions, such as when sediment loads aren’t uniform or where channels take on different shapes than those assumed in the theory.
Examples & Analogies
This is akin to following a diet plan designed for a certain type of body. While it might work well for that body type, it may not be effective for everyone. Lacey's theory offers great insights but might not address all scenarios or variations.
Comparison between Kennedy’s and Lacey’s Theories
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
| Aspect | Kennedy’s Theory | Lacey’s Theory |
|---|---|---|
| Developed by | R.G. Kennedy (1895) | G. Lacey (1930) |
| Based on | Upper Bari Doab Canal | Various canal systems |
| Type | Semi-empirical | Empirical |
| Focus | Critical velocity for non-silting section | Regime flow with stable sediment load |
| Sediment factor | Critical velocity ratio (m) | Silt factor (f) |
| Channel slope | Not directly addressed | Explicitly given |
| Wetted perimeter | Not considered | P = 4.75 Q |
| Limitations | Limited data, no slope | Based on specific sediment sizes. |
Detailed Explanation
This comparison highlights the key differences between Kennedy's and Lacey's theories. It emphasizes the different origins and empirical bases of the two theories, illustrating how Lacey's work built upon and refined Kennedy’s assumptions, making it more suitable for wider applications in civil engineering.
Examples & Analogies
Think of it like comparing two different sports coaches. Coach Kennedy has a specialized approach based on a single team's performance, while Coach Lacey uses insights from multiple teams, making him adaptable and comprehensive in his strategies; hence, Lacey is seen as more widely applicable in various conditions.
Modern Developments and Relevance
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Although Kennedy’s and Lacey’s theories laid the foundation for channel design in alluvial soils, modern techniques now use:
• Computational Fluid Dynamics (CFD)
• Sediment transport models
• GIS-based channel simulation
• Machine learning for sediment rating curves
However, for conceptual understanding and preliminary design, Kennedy’s and Lacey’s theories are still included in civil engineering curricula and design handbooks due to their simplicity and practical value.
Detailed Explanation
This concluding section indicates that while modern engineering has advanced with new technologies and methods, Kennedy’s and Lacey’s theories remain relevant as foundational educational tools. They provide simple, initial insights into channel design before more complex simulations and modeling techniques are applied.
Examples & Analogies
It's similar to learning basic math before diving into complex calculus. Those foundational theories (like simple addition and subtraction) provide vital stepping stones for understanding more intricate concepts in engineering.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Regime Channels: Channels that achieve stability over time with respect to sediment transport.
-
Kennedy’s Theory: Focuses on the relationship between critical velocity and channel characteristics based on empirical observations.
-
Lacey’s Theory: Provides empirical equations that broaden the understanding of channel dynamics and facilitate proper design.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The design of irrigation channels in the Punjab region is an application of Kennedy's theory, taking empirical data from the Upper Bari Doab Canal.
-
Lacey's equations are utilized in the design of channels to ensure efficient sediment transport in various alluvial systems.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Stability in flow, no silt will show, that's what a regime channel can bestow.
📖 Fascinating Stories
-
Imagine a river named 'Regino' flowing smoothly with no weeds or silt—this is how a regime channel should behave, embodying stability.
🧠 Other Memory Gems
-
Remember 'I-Q-T' for the stages of regime channels: Initial, Quasi, True.
🎯 Super Acronyms
Use 'C-V' for Critical Velocity, the key to keeping sediment at bay!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Regime Channel
Definition:
A channel that maintains a stable shape, slope and flow with consistent discharge and sediment load over time.
-
Term: Critical Velocity (Vc)
Definition:
The minimum velocity required to prevent silting in a channel.
-
Term: Initial Regime
Definition:
The immediate response stage of a canal when first put into use.
-
Term: True Regime
Definition:
The final equilibrium state of a channel achieved over time.
-
Term: Silt Factor (f)
Definition:
A coefficient that accounts for the sediment load in the channel.