Enrol to start learning
Reading is open to everyone. Enrolling is free, and it is what unlocks the audio lessons, practice tests and progress tracking.
1. What is a Geometric Sequence?
Interactive Audio Lesson
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free account
Today, we're diving into an essential part of mathematics called geometric sequences. Can anyone tell me what a geometric sequence is?
Is it a sequence where you keep adding a number to each term?
Good guess, but it's actually where each term is found by multiplying the previous term by a common ratio, denoted by r. If we were to look at the sequence 2, 6, 18, 54, what's the common ratio?
I think it's 3 because if you multiply 2 by 3, you get 6.
Exactly! The common ratio is 3. Remember, geometric sequences involve multiplication, not addition. Let's remember this with the mnemonic 'Multiply to Grow'.
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free account
Now, let's learn how to find any term in a geometric sequence. We use the formula T = ar^(n−1). Can anyone explain what each part stands for?
I think a is the first term, and n is the term's position.
Correct! And r is the common ratio. Let’s find the 5th term in our sequence from before, where a = 2 and r = 3.
So, T = 2 * 3^(5−1)? That would equal 2 * 81, which is 162!
Great job! Keep in mind: 'First times Ratio for the nth Term'.
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free accountNext, let’s explore how to calculate the sum of the first n terms, known as a finite geometric series. Does anyone remember the formula?
Is it S = a * (1 − r^n) / (1 − r)?
Exactly right! Let's use this formula to find the sum of the first 5 terms where a = 2 and r = 3.
So, S = 2 * (1 - 3^5) / (1 - 3) = 2 * (-242)/(-2) = 242!
Well done! Always visualize it as 'Sum is a Multiplier' to remember the steps.
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free accountNow, who can tell me what happens with an infinite geometric series?
I think those are sequences that go on forever, right?
Exactly! However, it only converges to a finite sum if the absolute value of r is less than 1. How do we calculate the sum of an infinite series?
I believe the formula is S = a / (1 − r) for |r| < 1?
That's correct! Remember 'Infinite Sum is Limited'. Let’s apply that to find the sum of the series 5 + 2.5 + 1.25 + ... .
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free accountFinally, let’s look at how we can apply geometric sequences in real life, like in finance, through compound interest. Who knows the formula for total amount A after n years?
Is it A = a * (1 + r)^n?
Yes! If you invested $1,000 at 5% interest compounded annually for 3 years, how much will you have?
A = 1000 * (1 + 0.05)^3 equals approximately $1157.63!
Fantastic! Remember 'A is Amount After Interest', a great way to visualize financial growth!
Reference YouTube Videos
Audio Book
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountA geometric sequence is a list of numbers where each term is obtained by multiplying the previous term by the same constant. This constant is called the common ratio, denoted by 𝑟.
Detailed Explanation
A geometric sequence is defined as a sequence of numbers formed by multiplying each term by a consistent value known as the common ratio. This means if you start with a number (the first term) and repeatedly multiply it by a specific number, you will generate the sequence. For example, if your first term is 2 and your common ratio is 3, the sequence will be 2, 6, 18, 54, etc.
Examples & Analogies
Imagine a plant that grows by doubling its height every week. If it starts at 1 inch, after one week it will be 2 inches, after two weeks it will be 4 inches, and so forth. Each week, the height is multiplied by the same factor, illustrating a geometric sequence in action.
Key Concepts
Core takeaways and short definitions to help you quickly recall the key ideas from this section.
Geometric Sequence: A sequence generated by multiplying the previous term by a constant ratio.
Common Ratio: A fixed number used to multiply each term in a geometric sequence to obtain the next term.
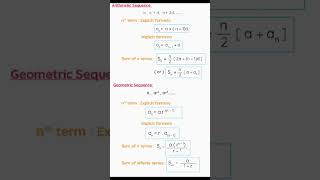
n-th Term Formula: T = ar^(n−1) provides a method to find any specific term in the sequence.
Sum of a Finite Series: The total of a defined number of terms in a geometric sequence can be calculated with S = a(1 - r^n) / (1 - r).
Infinite Series: An infinite geometric series converges to a finite sum if |r| < 1, calculated with S = a / (1 - r).
Examples
Step-by-step examples to apply the section's ideas and test your understanding.
Example of a geometric sequence: Starting with 2 and a common ratio of 3, the sequence is 2, 6, 18, 54.
To find the 4th term where a = 4 and r = 2: T = 4 * 2^(4−1) = 4 * 8 = 32.
A geometric series example: Calculate the sum of the first 5 terms for 4, 8, 16, 32, 64.
Memory Aids
Interactive tools to help you remember key concepts
Stories
Flash Cards
Glossary
Geometric Sequence
A sequence of numbers where each term after the first is obtained by multiplying the previous term by a constant called the common ratio.
Common Ratio (r)
The constant factor between consecutive terms in a geometric sequence, derived by dividing any term by its preceding term.
nth Term
The term at position n in a sequence, found using the formula T = ar^(n−1).
Finite Geometric Series
The sum of a specific number of terms of a geometric sequence.
Infinite Geometric Series
An infinite geometric sequence that can have a finite sum only when |r| < 1.