Concept of the Derivative
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Derivatives
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we’re diving into the concept of derivatives. Can anyone tell me what a derivative represents?

Is it something about how a function changes?

Exactly! The derivative measures how a function changes with respect to its input. Geometrically, it represents the slope of the tangent line to the curve.

So, it's like how steep the curve is at any point?

Yes! And physically, if we think of distance versus time, the derivative gives us the velocity. A mnemonic to remember is 'DVC' – Derivative for Velocity of Change.

What’s the formal way to define a derivative?

"Great question! The derivative at a point x = a is defined using a limit. It’s given by the expression
Definition of the Derivative
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's delve deeper into the limit definition of the derivative. Who can remind us what the difference quotient is?

It's the fraction where you find the change in the function value over the change in x.

Correct! The difference quotient, $$\frac{f(a+h) - f(a)}{h}$$ shows the average rate of change over an interval. As h gets smaller, this becomes closer to the slope of the tangent line.

Can you show us an example of this limit in action?

"Of course! Let's consider the function f(x) = x^2. To find the derivative at a point x = a, we calculate:
Basic Differentiation Rules
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s move on to some basic rules of differentiation. Can anyone list a couple of the rules we've learned?

There’s the constant rule and the power rule!

Exactly! The constant rule states that the derivative of a constant is zero. The power rule tells us that if f(x) = x^n, then f'(x) = nx^{n-1}.

Are there any rules for adding or subtracting functions?

Good thinking! Yes, for functions f(x) = g(x) ± h(x), we have: f'(x) = g'(x) ± h'(x).

And what about multiplying by constants?

For sure! If f(x) = c·g(x), where c is a constant, then f'(x) = c·g'(x). Always remember the acronym 'CLAP' for Constant, Limit, Addition, Power.

To summarize, basic differentiation rules include the constant rule (0), power rule (nx^{n-1}), sum and difference rules, and constant multiple rule.
Applications of Derivatives
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let’s discuss applications of derivatives. Where might we encounter derivatives outside of math?

In physics, especially in motion, right?

Perfect! In physics, if we denote distance as s(t), the derivative s'(t) gives us the velocity, which is a rate of change.

I heard we also use derivatives to find maxima and minima in functions?

Exactly! By finding where the derivative equals zero, we locate critical points that help us determine local maxima and minima.

How about in real-world scenarios, can you give an example?

Sure! In economics, derivatives can help determine marginal cost, which informs production decisions. You’d find the derivative of the cost function with respect to quantity.

To summarize, derivatives are essential for measuring rates of change, finding maxima and minima, and applying mathematical concepts to real-world scenarios.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section introduces the concept of the derivative, focusing on its definition as the limit of the difference quotient, its geometric interpretation as the slope of the tangent line, and its physical significance in terms of rates of change, such as velocity.
Detailed
Detailed Summary
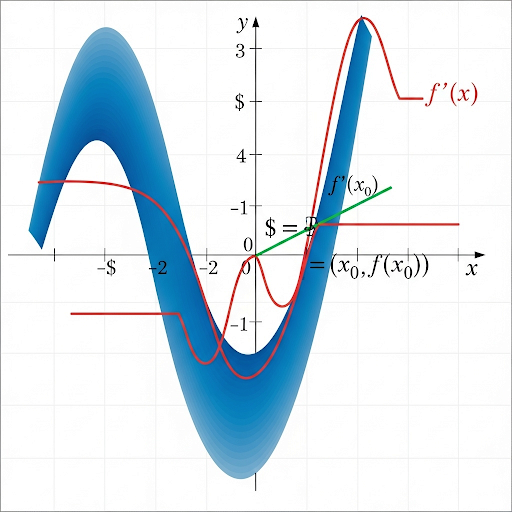
The derivative, denoted as f'(x) or df/dx, is one of the core concepts of calculus that quantifies how a function changes as its input changes. In geometric terms, it represents the slope of the tangent line to the curve y = f(x) at any given point. For instance, if f(x) describes the distance traveled over time, the derivative measures the velocity or rate of change of that distance with respect to time.
The formal definition of the derivative at a point x = a is provided by the limit:
$$f'(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h}$$
This difference quotient captures the average rate of change of the function as h approaches zero. The section also covers basic differentiation rules such as the power rule, constant rule, sum and difference rules, and constant multiple rules, which facilitate the computation of derivatives quickly. Lastly, the importance and applications of derivatives in analyzing rates of change, finding maximum and minimum values of functions, and solving practical problems in physics and engineering are also discussed.
Youtube Videos




Audio Book
Dive deep into the subject with an immersive audiobook experience.
What is a Derivative?
Chapter 1 of 1
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Consider a function 𝑓(𝑥) that describes some quantity depending on 𝑥. The derivative of 𝑓(𝑥), denoted by 𝑓′(𝑥) or \( \frac{d}{dx} f(x) \), measures how 𝑓(𝑥) changes when 𝑥 changes by a very small amount.
- Geometrically, the derivative at a point is the slope of the tangent line to the curve 𝑦 = 𝑓(𝑥) at that point.
- Physically, if 𝑓(𝑥) represents distance over time, the derivative represents velocity.
Detailed Explanation
To understand what a derivative is, think of a function as a formula that describes a relationship between two quantities. The derivative tells us how quickly the output of this function changes in relation to changes in the input. For example, if you have a function that describes your distance traveled over time, the derivative of that function would provide the speed at which you are traveling at any given moment. The slope of the tangent line can help visualize this; it's similar to how steep a hill is at any point—steeper hills have larger slopes, just like a quick change in distance suggests higher speed.
Examples & Analogies
Imagine you're surfing on a wave. If you're moving smoothly, it feels nice and steady; this is like a function that changes gradually. The derivative is like your surfboard's tilt; when you tilt more (a larger slope), you go faster. So, the more you tilt, the quicker you respond to the wave, much like how derivatives let us measure change in speed or direction.
Key Concepts
-
Derivative: The instantaneous rate of change of a function.
-
Difference Quotient: The formula used to find the derivative via limits.
-
Tangent Line: A line that represents the slope of the function at a certain point.
-
Power Rule: A rule for finding the derivative of power functions.
-
Applications: Derivatives' roles in real-world scenarios like physics and optimization.
Examples & Applications
Example 1: If f(x) = x^2, then f'(x) = 2x by using the power rule.
Example 2: If f(x) = 3x^3 - 4x + 2, then f'(x) = 9x^2 - 4.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To find the slope that’s neat, take the limit, no defeat.
Stories
Imagine a race car that speeds up and slows down; derivatives help drivers understand how fast they're going at any moment.
Memory Tools
DVC – Derivative for Velocity of Change helps recall that derivatives relate to rates of change.
Acronyms
CLAP - Constant, Limit, Addition, Power for basic differentiation rules.
Flash Cards
Glossary
- Derivative
A measure of how a function changes as its input changes; it represents the slope of the tangent line at a given point.
- Difference Quotient
The expression \frac{f(a+h) - f(a)}{h} used in the limit definition of the derivative.
- Limit
A mathematical concept that describes the behavior of a function as its input approaches a certain value.
- Slope
The steepness of a line, calculated as the change in the y-value divided by the change in the x-value.
- Tangent Line
A straight line that touches a curve at a single point without crossing it, representing the instantaneous rate of change.
Reference links
Supplementary resources to enhance your learning experience.
