Critical Points and Turning Points
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Critical Points
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are going to discuss critical points. A critical point occurs where the first derivative of a function is zero or undefined. Do you remember what a derivative indicates?

It measures how a function is changing, right?

Exactly! And when the derivative is zero or undefined, it suggests that the function may have a maximum or minimum point. Why do you think this is important?

It helps us understand the behavior of the function!

Precisely! Remember the acronym **CUP** for Critical points lead to Understanding Peaks (maxima) and Valleys (minima).
Identifying Turning Points
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s talk about turning points. What do you think they are?

I think they are points where the function changes direction!

Correct! There are two types of turning points: local maxima and local minima. Can anyone tell me how to identify these using the first derivative?

If the first derivative changes from positive to negative, it's a local maximum, right?

Exactly! And if it changes from negative to positive, that's a local minimum. Keep in mind: **Maxima are at the top, minima are at the bottom.**
Applying the First Derivative Test
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

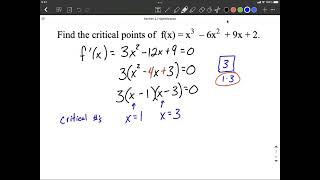
Now that we know what critical points and turning points are, let's explore the First Derivative Test. Can someone explain its steps?

We need to find the first derivative and set it to zero to find critical points!

Yes! And what do we do next?

We check if the derivative changes from positive to negative or vice versa.

Perfect! Remember the phrase **Positive to Negative = Peak; Negative to Positive = Pit** to recall the patterns.
Utilizing the Second Derivative Test
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's move on to the Second Derivative Test. Who can summarize when we use this test?

We use it when the first derivative is zero, right?

Exactly! What do we look for with the second derivative?

If it's greater than zero, we have a minimum, and if it's less than zero, we have a maximum!

Exactly! So remember: **Second Derivative = Shape of the Graph.** If it's positive, the graph is concave up, and it's a minimum. If it's negative, concave down, so it's a maximum.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Critical points are where a function's first derivative equals zero or is undefined, indicating potential turning points where the function changes direction. The section emphasizes methods for identifying and classifying these points, including the first and second derivative tests.
Detailed
Critical Points and Turning Points
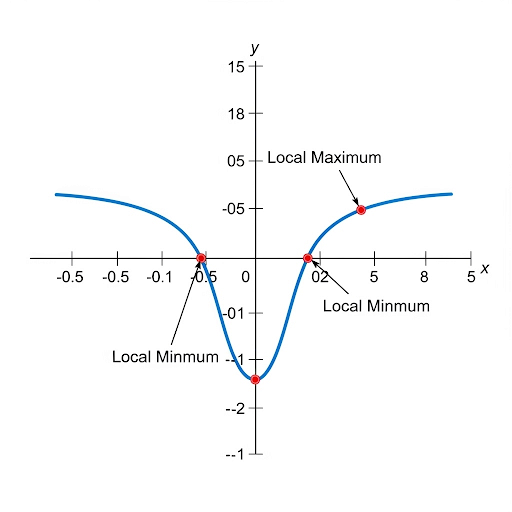
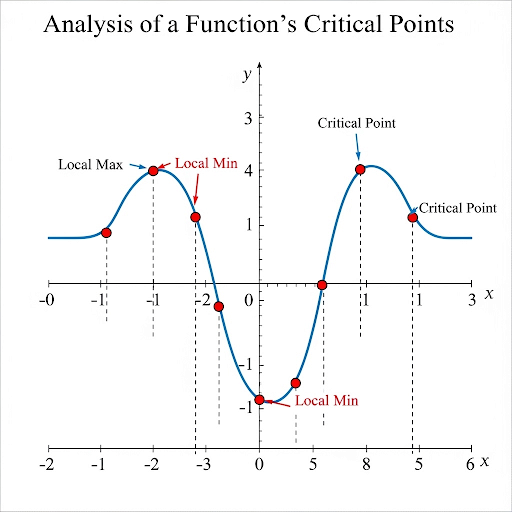
In calculus, critical points of a function, defined as locations where the first derivative is either zero or undefined, are essential in determining the function's local maxima and minima. A turning point signifies a change in direction of the function's graph, essential for optimization problems. This section categorizes turning points into local maxima, where the function peaks locally, and local minima, representing the lowest points locally. The First Derivative Test and Second Derivative Test are introduced as methods for determining the nature of these critical points. Mastery of these concepts is key for solving real-world optimization problems, such as maximizing areas or understanding the behavior of economic models.
Youtube Videos

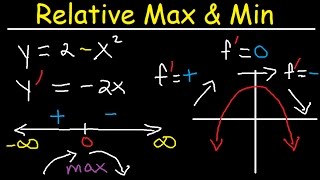



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Critical Points
Chapter 1 of 1
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A critical point of a function 𝑓(𝑥) occurs where the first derivative 𝑓′(𝑥) = 0 or is undefined.
Detailed Explanation
A critical point is a specific location on the graph of a function where the slope is either zero or doesn't exist. This is important because these points could indicate where the function reaches its maximum or minimum values. To find these points, we look for values of x that make the first derivative (which represents the slope of the function) equal to zero or undefined.
Examples & Analogies
Think of a car driving along a hilly road. When the car reaches the peak of a hill (maximum point) or the dip in a valley (minimum point), it may temporarily come to a stop (slope = 0). These points where the car is neither going up nor down correspond to critical points in the function's graph.
Key Concepts
-
Critical Point: A key location in a function's behavior where the derivative is zero or undefined.
-
Turning Point: The point at which a function changes direction.
-
Local Maximum: The peak of a function in a local neighborhood.
-
Local Minimum: The lowest point of a function in a local neighborhood.
Examples & Applications
Example for Maximum: For f(x) = x² - 4x + 3, critical point at x = 2 shows a local minimum at (2, -1).
Example for Minimum: For f(x) = -x³ + 3x² + 9, critical points at x = 0 (local min) and x = 2 (local max).
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
If the slope is flat, time to chat; max or min, let's begin!
Stories
Once upon a time, a little hill stood tall—max at the peak, but fell to the ball.
Memory Tools
For maxima think 'M' for mountain—minima think 'V' for valley.
Acronyms
Use **CUM** to remember
Critical Points give us Up or Down.
Flash Cards
Glossary
- Critical Point
A point where the first derivative of a function is zero or undefined.
- Turning Point
A point on a graph where the function changes direction.
- Local Maximum
A point where a function reaches a peak locally.
- Local Minimum
A point where a function reaches a valley locally.
- First Derivative Test
A method to determine where a function changes from increasing to decreasing or vice versa.
- Second Derivative Test
A method to determine the concavity of a function to classify local maxima and minima.
Reference links
Supplementary resources to enhance your learning experience.
