Learn
Games

2.3 - Factorisation of Polynomials

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Understanding Factorisation

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Welcome class! Today we will discuss the factorisation of polynomials. First, can anyone tell me what factorisation means in mathematics?

Student 1
Student 1

I think it means breaking something down into smaller parts.

Teacher
Teacher

Exactly! Factorisation involves expressing an algebraic expression, like a polynomial, as a product of simpler factors. Why do you think this is important?

Student 2
Student 2

It helps solve equations more easily?

Teacher
Teacher

Correct! By breaking down polynomials, we can find solutions to equations more efficiently. Let's discuss common methods of factorisation.

Methods of Factorisation

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

There are several techniques for factorisation. Can anyone name one?

Student 3
Student 3

Taking out common factors!

Teacher
Teacher

Great! Taking out common factors is usually the first step. Can someone give an example?

Student 4
Student 4

What about 6x² + 9x? You can factor out 3x, right?

Teacher
Teacher

Exactly! It would become 3x(2x + 3). Now, another method is splitting the middle term, can someone explain that?

Splitting the Middle Term

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Let’s dive deeper into splitting the middle term. For a polynomial like x² + 7x + 10, how would you factor that?

Student 1
Student 1

I think you should split 7 into 5 and 2?

Teacher
Teacher

Right! So we rewrite it as x² + 5x + 2x + 10. What’s next?

Student 2
Student 2

Group them into two parts and factor out common factors!

Teacher
Teacher

Exactly! That gives us x(x + 5) + 2(x + 5). Now, can you combine those factors?

Applying Identities

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Finally, let’s discuss using identities. Does anyone recall the identity for (a + b)²?

Student 3
Student 3

(a + b)² = a² + 2ab + b²!

Teacher
Teacher

Perfect! This identity helps in factorising expressions quickly. Can someone think of how it could apply here?

Student 4
Student 4

We could use it to factor something like x² + 6x + 9!

Teacher
Teacher

Exactly! That factors to (x + 3)². Let’s remember these identities—they are powerful tools!

Recap and Practice

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

To wrap up, can anyone summarize the methods of factorisation we covered today?

Student 1
Student 1

We can take out common factors, split the middle term, and use identities!

Teacher
Teacher

Correct! Now, let's practice with some problems based on these methods.

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

This section covers the concept of factorising polynomials, essential for simplifying algebraic expressions and solving equations.

Standard

In this section, we explore the process of factorising polynomials, which involves expressing a polynomial as a product of its factors. Key methods include taking out common factors, splitting the middle term, and applying polynomial identities.

Detailed

Factorisation of Polynomials

Factorisation of polynomials is a fundamental algebraic technique that transforms a polynomial expression into a product of simpler factors. This approach is integral to various algebraic processes, including simplifying expressions, solving equations, and understanding polynomial behaviors. Several methods can be employed for factorisation:

  • Taking Out Common Factors: Identify and extract the greatest common factor shared among the terms.
  • Splitting the Middle Term: This method particularly applies to quadratics where the middle term can be broken down into two terms, facilitating factorisation.
  • Using Identities: Familiarity with algebraic identities (like
  • (a+b)² = a² + 2ab + b²) can simplify factorisation efforts dramatically.

Example: To factorise the polynomial x² + 7x + 10:
1. Split the middle term: x² + 5x + 2x + 10 = x(x + 5) + 2(x + 5).
2. Combine the grouped factors: = (x + 2)(x + 5).

Understanding these techniques empowers learners to tackle more complex polynomial expressions effectively.

Youtube Videos

Factorisation of Polynomials in One Shot (Full Chapter) | ICSE Class 10 Math | Board 2022 | Vedantu
Factorisation of Polynomials in One Shot (Full Chapter) | ICSE Class 10 Math | Board 2022 | Vedantu
Factor Theorem Factorization | Factorisation of Polynomials ICSE Class 10 | @sirtarunrupani
Factor Theorem Factorization | Factorisation of Polynomials ICSE Class 10 | @sirtarunrupani
Factor Theorem Factorization | Factorisation of Polynomials ICSE Class 10 | @sirtarunrupani
Factor Theorem Factorization | Factorisation of Polynomials ICSE Class 10 | @sirtarunrupani
Factorization in One Shot | Maths - Class 8th | Umang | Physics Wallah
Factorization in One Shot | Maths - Class 8th | Umang | Physics Wallah
Polynomials Class 9 in One Shot 🔥 | Class 9 Maths Chapter 2 Complete Lecture | Shobhit Nirwan
Polynomials Class 9 in One Shot 🔥 | Class 9 Maths Chapter 2 Complete Lecture | Shobhit Nirwan
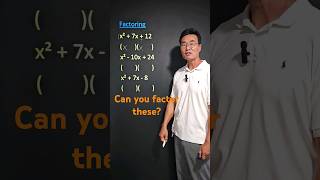
Basic Factoring
Basic Factoring
Shortest Trick to Solve Quadratic Equation #youtubeshorts
Shortest Trick to Solve Quadratic Equation #youtubeshorts
Factorization of Algebraic Expressions | Factorization Class 8 | Factorization Method | Factorize
Factorization of Algebraic Expressions | Factorization Class 8 | Factorization Method | Factorize
Polynomials Class 10 One Shot | Educart 9th & 10th
Polynomials Class 10 One Shot | Educart 9th & 10th
Splitting the Middle Term | Splitting the middle term tricks | Factorisation by Splitting the middle
Splitting the Middle Term | Splitting the middle term tricks | Factorisation by Splitting the middle

Audio Book

Dive deep into the subject with an immersive audiobook experience.

Understanding Factorisation

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

● Factorising a polynomial means writing it as a product of its factors.

Detailed Explanation

Factorisation is the process of breaking down a polynomial into simpler components called factors. When we say that we 'factorise' a polynomial, we mean that we want to express it in the form of a product. For example, instead of having a quadratic expression like x² + 5x + 6, we want to express it as a product of two binomials (like (x + 2)(x + 3)). This makes it easier to work with, especially when solving equations.

Examples & Analogies

Think of factorisation like breaking down a complex puzzle into smaller pieces. Just as a finished puzzle is often easier to visualize when you can see the smaller interlocking pieces, a polynomial can be understood more easily when it is presented as a product of its factors.

Methods of Factorisation

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

● Common methods:
○ Taking out common factors
○ Splitting the middle term
○ Using identities like:
(a+b)²=a²+2ab+b²

Detailed Explanation

There are several techniques used for factorising polynomials:
1. Taking out common factors: This involves finding the greatest common factor (GCF) of the terms in the polynomial and factoring it out. For instance, in the polynomial 4x² + 8x, the GCF is 4x.
2. Splitting the middle term: This technique is often used in quadratic polynomials to turn the middle term into two separate terms that can be factored.
3. Using identities: Certain algebraic identities help in factorising. For example, the identity for squares states that (a + b)² = a² + 2ab + b² can help in identifying and rewriting polynomials that fit this pattern.

Examples & Analogies

Consider methods of factorisation like different tools in a toolbox. Just as you might use a hammer for nails but a screwdriver for screws, you would choose different methods of factorisation depending on the structure of the polynomial you're dealing with.

Example of Factorising a Polynomial

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

● Example:
Factorise:
x² + 7x + 10
Solution:
Split middle term:
x² + 5x + 2x + 10 = x(x + 5) + 2(x + 5) = (x + 2)(x + 5)

Detailed Explanation

In this example, we want to factor the polynomial x² + 7x + 10. First, we look for two numbers that multiply to give us 10 (the constant term) and add up to 7 (the coefficient of the middle term). The numbers 5 and 2 work because 5 * 2 = 10 and 5 + 2 = 7. We can then rewrite the polynomial as x² + 5x + 2x + 10. Next, we group the terms: (x² + 5x) + (2x + 10) gives us factors; from the first group we can factor out x, leading us to x(x + 5). From the second group, factoring out 2 gives us 2(x + 5). Since both groups contain the common factor (x + 5), we can write the final factorised form as (x + 5)(x + 2).

Examples & Analogies

Factorising can be likened to finding ingredients for a recipe. If you have a complex dish (the polynomial), you may break it down into simpler components (the factors). Just like in cooking, understanding the relationship between different ingredients makes the final dish easier to prepare.

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Factorisation: Expressing a polynomial as a product of simpler factors.

  • Common Factors: Factors that are shared among terms in a polynomial.

  • Splitting the Middle Term: A method for factoring quadratics where the middle term is divided into two parts.

  • Polynomials Identities: Using known identities for easier factorisation.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • Factor the polynomial x² + 7x + 10 by splitting the middle term to (x + 2)(x + 5).

  • Rewrite the polynomial 6x² + 9x as 3x(2x + 3) by taking out common factors.

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • If factor you must, take the common first; it’s a method that’s tried, you’ll never be cursed.

📖 Fascinating Stories

  • Once there was a polynomial who wanted to break free. It found its common factor and danced with glee, splitting its middle term led to a brand new identity.

🧠 Other Memory Gems

  • F.A.C.T – Factor, Ask for common, Check the middle, Take identities.

🎯 Super Acronyms

F.C.M.I – F for Factor Out, C for Common Factor, M for Middle Term, I for Identity.

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: Factorisation

    Definition:

    The process of expressing a polynomial as a product of its factors.

  • Term: Polynomial

    Definition:

    An algebraic expression that involves variables raised to whole number powers.

  • Term: Common Factor

    Definition:

    A factor that is common to all terms of the polynomial.

  • Term: Middle Term

    Definition:

    The second term in a trinomial; important for certain factorisation methods.

  • Term: Identity

    Definition:

    A mathematical equality that holds for all values of the involved variables.