ICSE Class 12 Maths Chapter 8 Application of Calculus
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
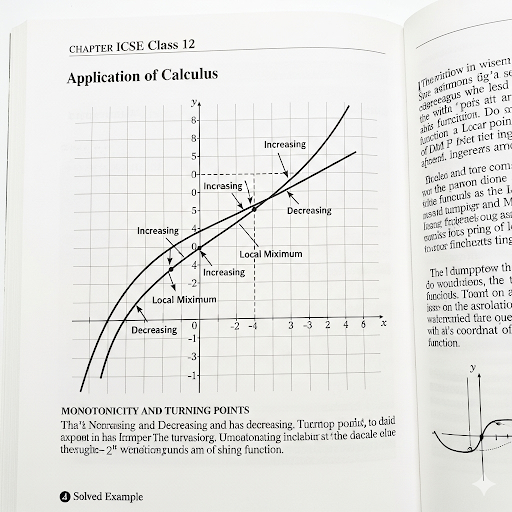
Increasing and Decreasing Functions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's begin with increasing and decreasing functions. A function is increasing on an interval if its derivative is positive.

How do we know where the function is increasing or decreasing?

Good question! We determine that by calculating the derivative. If the first derivative, f prime of x, is greater than 0, the function is increasing.

What if f prime of x is less than 0?

In that case, the function is decreasing on that interval. Remember: Positive means 'up', and negative means 'down'.

Can you give us an example?

Certainly! For the function f(x) = 3x^2 - 12x + 5, we first find its derivative.

So, we have f prime of x equals 6x - 12. Setting that to zero, we find x equals 2. Then we analyze the intervals around that point.

So for x less than 2, it's decreasing, and for x greater than 2, it's increasing?

Exactly! Great job! So, f(x) is decreasing on (-∞, 2) and increasing on (2, ∞).

In summary, a positive derivative indicates an increasing function, while a negative derivative indicates a decreasing one.
Maxima and Minima
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's discuss maxima and minima. What do you think these terms mean?

Are they points where the function reaches its highest or lowest value?

That's right! A local maximum occurs where the function changes from increasing to decreasing, and vice versa for a local minimum.

How do we find those points?

We use the first derivative test. If f prime of x changes from positive to negative, it's a maximum.

What about the second derivative?

Great insight! The second derivative test tells us if it's a maximum or minimum based on its sign.

Let's find the local maxima and minima for f(x) = x^3 - 6x^2 + 9x + 2.

First, we get the derivative: f prime(x) = 3x^2 - 12x + 9, and set it to zero for x = 1, 3.

And then we check the second derivative?

Exactly! If f double prime(1) is negative, we have a maximum at x = 1. For x = 3, if it's positive, we have a minimum.

In summary, we find critical points using f prime, and analyze them with f double prime for maxima and minima.
Application of Maxima and Minima
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s apply this knowledge to real-world problems. Can you think of how calculus is used for optimization?

Like calculating the maximum area of a rectangle?

Exactly! If we know the perimeter of a rectangle, we can maximize the area by applying what we learned.

How do we set that up?

We use the formula for the perimeter, P = 2(x + y). With P = 20, we have x + y = 10. Substituting y gives us A = x(10 - x).

And to maximize the area?

We find the derivative of A, set it to zero, and determine when the second derivative is negative to find maximum.

So the maximum area would occur at a square shape?

Absolutely! In summary, we apply maximum and minimum techniques to solve real-world problems like finding optimal dimensions.
Rate of Change
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Finally, let’s discuss the rate of change. What does the derivative represent?

Is it how fast something is changing?

Exactly! It tells us how a quantity changes relative to another. For example, velocity is the rate of change of displacement.

Can you give another example?

Sure! Marginal cost is the rate of change of total cost concerning the quantity produced. It helps businesses understand costs better.

What about in terms of geometry?

Great question! For a sphere, if we know the radius is changing, we can find the rate of change of volume using derivatives.

In summary, derivatives provide insight into how things change, crucial for various fields.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we delve into the applications of calculus focusing on increasing and decreasing functions, the first and second derivative tests for maxima and minima, and the optimization of real-life scenarios such as area and volume. The significance of calculus in maximizing or minimizing various quantities for practical decision-making is emphasized.
Detailed
Detailed Summary
This section covers the essential applications of calculus in mathematics, particularly concerning functions. It begins with increasing and decreasing functions, where we define a function's behavior based on its derivatives, linking it to the concept of rate of change. The next part discusses maxima and minima, providing the criteria for identifying local maximum and minimum points using both first and second derivative tests. The application of these concepts extends to real-life problems, such as optimizing area, cost, or revenue, where calculus helps in effective decision-making. Lastly, we explore the rate of change, showcasing its importance in various fields, including physics and economics, through practical examples.
Youtube Videos

Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Calculus
Chapter 1 of 1
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Calculus is one of the most powerful tools in mathematics, and its applications stretch across science, economics, engineering, and daily life. In this chapter, we explore how differential calculus is used to solve practical problems involving rate of change, maxima and minima, and increasing/decreasing functions. Understanding the application of calculus helps students not only in exams but also in real-life decision-making situations where optimization is needed — for example, minimizing cost, maximizing profit, or finding the fastest route.
Detailed Explanation
This introduction highlights the significance of calculus in various fields. It emphasizes that calculus isn't just an academic subject but a practical tool used for real-life applications. Key concepts like rate of change and optimization are introduced, showing how they can help solve everyday problems such as cost reduction or profit maximization.
Examples & Analogies
Imagine you're running a business and want to know how to price your product. By applying calculus, you can determine the price that maximizes your profits. This real-life scenario illustrates how understanding calculus leads to better decision-making, reflecting its valuable role in our daily lives.
Key Concepts
-
Increasing Functions: A function is increasing when its derivative is positive.
-
Decreasing Functions: A function is decreasing when its derivative is negative.
-
Maxima and Minima: Points at which a function takes local extremes, found using first and second derivative tests.
-
Application of Calculus: Techniques from calculus can be applied to solve real-world optimization problems.
-
Rate of Change: The speed at which a value changes with respect to time, found by the derivative.
Examples & Applications
Finding intervals of increase and decrease for the function f(x) = 3x^2 - 12x + 5 based on its derivative.
Optimizing the area of a rectangle with a fixed perimeter of 20 meters, leading to a maximum area of a square.
Using the derivative to calculate the rate of change of volume for a sphere with respect to its radius.
Max happens when slope flips + to –, so go uphill then down.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Increasing functions rise, with positive skies; Decreasing functions fall, with negative calls.
Stories
Imagine a mountain climb (maximum) versus a valley dip (minimum) where climbers decide how high to go and where it's safe!
Memory Tools
For Maxima and Minima, remember 'M&M' for searching for Peaks (maxima) and Valleys (minima).
Acronyms
D-R for Derivative-Rate
Where D is Derivative and R is Rate of change!
Flash Cards
Glossary
- Increasing Function
A function is increasing on an interval if for any two points x1 and x2 in that interval, x1 < x2 implies f(x1) < f(x2).
- Decreasing Function
A function is decreasing on an interval if for any two points x1 and x2 in that interval, x1 < x2 implies f(x1) > f(x2).
- Maxima
Points at which a function reaches a highest value locally.
- Minima
Points at which a function reaches a lowest value locally.
- Derivative
A measure used to find the rate at which a function is changing at any given point.
- Rate of Change
The speed at which a variable changes over time, represented by the derivative.
Reference links
Supplementary resources to enhance your learning experience.
