1. Reversed Carnot Cycle

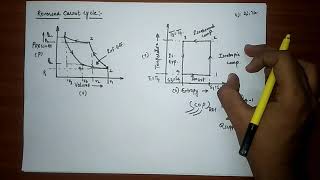
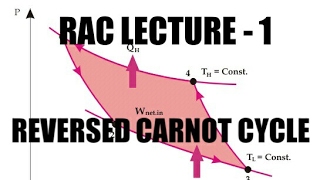
The reversed Carnot cycle is an ideal refrigeration cycle conceived for maximum theoretical efficiency. It uses air as the working fluid and consists of four reversible processes:

• Isothermal Heat Absorption (at low temperature, TL)
• Isentropic Compression
• Isothermal Heat Rejection (at high temperature, TH)
• Isentropic Expansion

The reversed Carnot cycle is a theoretical model used to describe the process of refrigeration. Its goal is to achieve maximum efficiency in cooling. The cycle includes four key processes:

1. Isothermal Heat Absorption: The system absorbs heat from a low-temperature source without changing the temperature, providing the initial cooling effect.
2. Isentropic Compression: The working fluid (air) is compressed, increasing its pressure and temperature without losing energy.
3. Isothermal Heat Rejection: The system releases heat to a high-temperature sink while maintaining a constant temperature.
4. Isentropic Expansion: The air expands, dropping in pressure and allowing for further cooling. Each of these processes plays a critical role in the cycle's efficiency.

Think of the reversed Carnot cycle like a highly efficient refrigerator. Imagine putting your groceries in the fridge on a hot day. The fridge takes in heat from inside (like the warm groceries), compresses it to handle the heat better, pushes the heat outside, and then creates a chilly space for your food to stay cool. However, like a superhero who needs perfect conditions to work, this cycle operates under idealized conditions that aren't always practical in real life.

COP (Coefficient of Performance): Highest possible for given temperature limits. COP for refrigeration: $\frac{T_L}{T_H - T_L}$ Limitation: Purely theoretical; requires isothermal processes (not practical with gases at large scales). Large, impractical equipment sizes and slow operation.

The efficiency of the reversed Carnot cycle is measured by the Coefficient of Performance (COP), which is defined as the ratio of the temperature of the cold source (TL) to the difference between the high temperature (TH) and the low temperature (TL). This gives the reversed Carnot cycle the highest theoretical COP compared to other refrigeration cycles. However, the cycle is primarily theoretical. In practice, achieving the perfectly isothermal processes required is very challenging, particularly for gases over large scales. Also, the equipment needed for this cycle tends to be large and cumbersome, making it impractical for everyday use. The slow operation of these systems further limits their applicability.

Imagine trying to set up a flawless air conditioning system in your home using only theoretical concepts. While it sounds perfect on paper (like our ideal unit), as soon as you try to build it, you find out you need a giant unit that takes forever to cool down the room. In the real world, we need to compromise for practicality, leading to designs that are efficient but not as perfect as the Carnot cycle suggests.

Limitation: Purely theoretical; requires isothermal processes (not practical with gases at large scales). Large, impractical equipment sizes and slow operation.

The limitations of the reversed Carnot cycle stem from its reliance on idealized processes. For it to function as intended, all heat transfer must occur isothermally, which is nearly impossible with gases in real-world scenarios. Additionally, the equipment required for this cycle tends to be too large for practical applications and operates slowly. Therefore, while it serves as an important theoretical benchmark, it cannot be effectively implemented in practical refrigeration systems.

Consider a recipe for a perfect cake that requires precise conditions and ingredients. If your kitchen doesn’t have the right tools or environment (like an ideal oven that maintains exact temperatures), you can’t recreate that perfect cake. Similarly, the reversed Carnot cycle outlines a 'perfect' refrigeration system, but the practical hurdles mean we often settle for less than the ideal scenario.

Serves as a benchmark for comparison with practical cycles. Not used in actual air refrigeration systems due to practical implementation challenges.

One of the main applications of the reversed Carnot cycle lies in its function as a theoretical benchmark. It provides a standard against which other, more practical refrigeration cycles can be compared. However, given the practical difficulties tied to its idealized processes, it is not used in real-life air refrigeration systems, where alternative cycles are preferred.

Think of the reversed Carnot cycle as a perfect score in an exam. While it sets a high standard for students, not every student can achieve that score. It serves as a measure of potential, helping students identify areas for improvement, just as the Carnot cycle helps engineers assess and improve real refrigeration technologies.

--