1. Definition

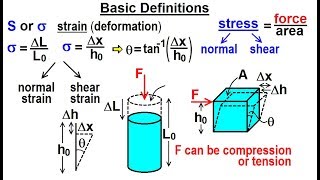
The shear center is defined as the point in the cross-sectional plane relative to which the net torque due to shear stress distribution (originating because of transverse load only) vanishes.

The shear center is a critical concept in structural mechanics, particularly when analyzing beams under transverse loads. It is the point where the application of shear force does not cause any twisting in the beam. Essentially, if you were to place the load at the shear center, the beam would solely bend without having any additional rotational motion. This concept is essential for engineers to consider when designing and analyzing structural components to ensure they maintain their intended shape and functionality under load.

Think of the shear center like the balancing point of a seesaw. If you sit exactly at the center, it will go up and down without tipping sideways. If you sit too far to one side, not only will it tilt, but it will also create a rotational motion. Just like in a seesaw, the shear center is where forces can be applied without causing twisting effects, allowing the structure to behave predictively.

Finding analytical formula for the location of the shear center for a general cross-section isn’t possible. However, the same can be derived for thin and open cross-sections such as the one in Figure 1.

For complex cross-sections, deriving a formula for the shear center is often impractical. However, for simpler geometries, like thin and open cross-sections, there are methods to ascertain its position. In practice, engineers often utilize graphical methods or computational tools to find the shear center for more complex shapes. This highlights the importance of understanding the principles behind shear centers, even if computational tools are used to find their exact locations.

Imagine trying to find the balance point of a weirdly shaped piece of wood. It’s much easier to find the balance point on a flat piece of cardboard than on a jagged rock. In engineering, many designs can be approximated as simple shapes like that cardboard, allowing for easier calculations, while more complex shapes might need extra tools, like a balance scale or computer software.

As the net torque about the shear center must be zero, we can first find the total moment about the shear center and then equate its x-component to zero.

In the context of shear centers, it's key to remember that for stability, the sum of forces and torques acting on the structure must equal zero. The net torque calculated about the shear center must be balanced; otherwise, the structure will twist. This leads to equations that help in determining the positions of the shear center by setting up the conditions where the torques cancel each other out. Understanding these dynamics is crucial for ensuring the structural integrity of beams.

Think of balancing a spinning top. For it to not fall over, the forces and rotational effects need to be in equilibrium. If a child pushes down on one side at an unequal angle, the top will begin to wobble and potentially fall. Similarly, if the forces on a beam are not balanced around the shear center, it leads to twisting and potential failure.

The formulas for shear center coordinates hold only if y and z axes are also the principal axes of the cross-section.

The principal axes are the axes about which the structure's moments of inertia are maximum or minimum, making them essential for analyzing shear centers. If the shear center formulas only apply when the principal axes coincide with the coordinate axes, it underscores the significant relationships between a shape's geometry and its mechanical properties. Knowing whether you're aligned with the principal axes can drastically simplify calculations and lead to correct applications in structural design.

You can visualize this with a tightrope walker. If they stand straight on the rope (aligned with their center of gravity) versus leaning or swaying (off-axis), their balance will be maintained only when centered. Similarly, for beams and structures, maintaining alignment with principal axes ensures stability under loads, preventing failure.

--