Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Euler-Bernoulli Beam Theory
Unlock Audio Lesson
Today, we will discuss the Euler-Bernoulli beam theory. Can anyone tell me what assumptions we make in this theory?
Does it assume that the beam's cross-section remains perpendicular to its centerline?
Exactly! The centerline tangent and the cross-section normal are aligned, which is crucial for the theory. Any other assumptions?
Is the axial displacement neglected in this theory?
Right! We assume that the axial displacement is negligible, simplifying the problem significantly. Let's remember this with the acronym 'CAT' - Centerline Aligned, Tangent aligned, Axial displacement neglected.
What’s the significance of these assumptions?
These assumptions allow us to derive a much simpler equation for beam deflection!
Can you summarize the equation for us?
Certainly! The governing equation is: $$ \frac{d^2y}{dx^2} = \frac{M(X)}{EI} $$. We will explore it more as we go.
Understanding Bending in Beams
Unlock Audio Lesson
Let’s discuss how bending moments relate to the curvature of a beam. Can someone explain this to us?
Isn’t curvature defined as the change in angle along the beam?
Yes! Curvature (κ) measures how sharply a beam bends. It's defined by the formula: $$ κ = \frac{d^2y}{dx^2} $$. Remember, as curvature increases, bending moment does too.
So M = EIκ includes how stiff the beam is at resisting bending?
Exactly! The bending moment M is proportional to the bending stiffness EI multiplied by the curvature κ.
Examples of Beam Theory Application
Unlock Audio Lesson
Let’s apply the theory to a practical example. Suppose we have a beam clamped at one end. What can we determine?
We can find the bending moment profile>
Correct! By applying equilibrium conditions, we derive the bending moment as a function of the distance from the support.
And the deflection at the free end can be calculated using that?
Yes! Using the governing equation, we get the deflection of the beam at any point, particularly at the end.
What are the conditions we set up for the equation?
Great question! We set boundary conditions where deflection is zero at the clamped end and the slope is also zero at that end.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the Euler-Bernoulli beam theory, detailing its assumptions, mathematical formulation, and practical applications in calculating beam deflections under various loading conditions. Key concepts include curvature, bending moments, and differential equations governing beam behavior.
Detailed
Euler-Bernoulli Beam Theory
The Euler-Bernoulli beam theory is essential for understanding beam behavior under various loads. It assumes that:
- The tangent to the beam's centerline and the normal to its cross-section are aligned.
- Axial displacement of the beam is negligible.
- The slope of the beam's centerline is also negligible.
These simplifying assumptions allow us to describe the bending of beams using the relationship between bending moment (M), bending stiffness (EI), and curvature (κ). The governing equation derived from this theory is:
$$ \frac{d^2y}{dx^2} = \frac{M(X)}{EI} $$
This second-order linear differential equation can be solved to find the beam's deflection under different loading conditions. Two examples illustrate the application of this theory where one beam is clamped, and another is simply supported, detailing the deflection calculations through boundary conditions.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Alignment of Centerline and Cross-Section Normals
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
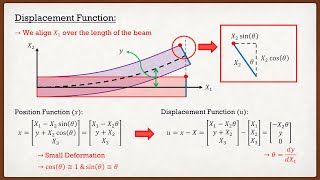
In this theory, it is assumed that the centerline tangent and the cross-section normal are aligned (see Figure 4b).
Detailed Explanation
The Euler-Bernoulli beam theory makes a crucial simplification by assuming that the direction in which the beam bends (the tangent of the centerline) is the same as the direction normal to the cross-section. This means when the beam bends, the cross-sections remain perpendicular to the centerline at any point, which simplifies the analysis significantly.
Examples & Analogies
Imagine a straighter-than-usual drinking straw. When you bend it, the top surface (cross-section) remains at a right angle to the line formed by the bent straw (centerline). This is similar to how the beam behaves under the assumptions of the Euler-Bernoulli theory.
Bending Moment and Curvature Relation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To get the required equations, we can invoke the following bending formula derived in an earlier lecture: M=EIκ.
Detailed Explanation
The equation M = EIκ relates the bending moment (M) acting on the beam to its curvature (κ), where E is the modulus of elasticity and I is the moment of inertia of the beam's cross-section. This relationship is essential because it allows us to understand how the bending moment influences the beam's deformation.
Examples & Analogies
Think of bending a rubber band. The more you stretch it (apply a moment), the tighter the curve (increased curvature) becomes. In the same way, as the moment increases for a beam, the curvature increases, leading to greater bending.
Negligible Axial Displacement Assumption
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the Euler-Bernouli beam theory, the axial displacement is also assumed to be negligible.
Detailed Explanation
This assumption simplifies the analysis further by stating that the horizontal position (axial displacement) of any point along the beam does not change significantly when the beam bends. This means that the angle of the centerline bends without moving sideways.
Examples & Analogies
Picture a tightrope walker. As they sway side to side, the rope itself doesn't elongate in the horizontal direction. It remains mostly straight; similarly, the beam's axial displacement is minimal during bending.
Linear Curvature Relation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To linearize the above expression in deflection y, it is further assumed that the magnitude of the slope of the centerline is very small.
Detailed Explanation
This means that when the beam bends, the angle of the slope (the tangent of the curve) is small enough that we can approximate the curvature using just the deflection of the beam without needing complex calculations.
Examples & Analogies
Consider a gentle hill on a road. If the hill is subtle enough, you don't need to account for sharp changes; you can treat it as a straight line for simplicity when driving over.
Governing Equation of Euler-Bernoulli Beam Theory
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Substituting the above relation in equation (2), we get d²y / dx² = M(X) / EI.
Detailed Explanation
This derived equation, d²y / dx² = M(X) / EI, is a second-order ordinary differential equation that relates the deflection of the beam (y) at any point to the bending moment acting at that section (M(X)). It allows engineers to calculate how much the beam will deflect under a given load.
Examples & Analogies
Think about a trampoline. The deeper you push down (the more force you apply), the more the surface dips. Similarly, this equation shows how the force applied to the beam relates to how much it bends.
Boundary Conditions in Deflection Problems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We need two boundary conditions to solve it.
Detailed Explanation
Boundary conditions specify the behavior of the beam at its supports or ends. For example, if one end of the beam is fixed, the deflection at that point will be zero. These conditions are crucial for getting specific solutions to the differential equation derived.
Examples & Analogies
Imagine a swing. If one end is held tightly, the swing won’t droop there, just like a beam won’t deflect at a fixed support. The conditions help define how the beam behaves under loading.
Examples of Beam Deflection Calculations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
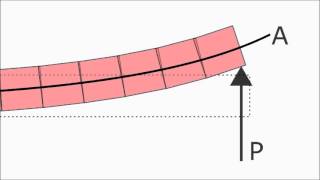
Suppose we have a straight beam which is clamped at one end and is subjected to a transverse load P at its other end.
Detailed Explanation
Here, the practical example illustrates how to use the Euler-Bernoulli beam theory to calculate the bending moment and deflection of the beam subjected to a transverse load. By cutting the beam at a certain point and analyzing equilibrium, we derive expressions that help in determining deflection due to the applied load.
Examples & Analogies
Think of a diving board. If you stand on the end of it, the board bends down due to your weight, and by applying this theory, you can predict how much it will bend based on your weight and the board's stiffness.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Euler-Bernoulli Beam Theory: A fundamental theory that describes the relationship between bending moments and beam deflections under loading.
-
Assumptions in Beam Theory: The crucial assumptions include alignment of cross-section normals with centerline tangents, negligible axial displacement, and small slope of the beam's centerline.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of a clamped beam: Analyzing deflection and bending moment under a transverse load at its free end.
-
Example of a simply supported beam: Understanding how to calculate bending moment due to a uniformly distributed load.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In beams so tall, we learn with ease, M and EI keep our bending at peace.
📖 Fascinating Stories
-
Imagine a chef carefully balancing the ingredients (bending moments) on a beam. The ratios (EI) need to be just right to keep everything balanced!
🧠 Other Memory Gems
-
CATS: Centerline, Axial displacement negligible, Tangent aligned, Slope negligible.
🎯 Super Acronyms
BEAM
- Bending equations
- Elasticity
- Axial alignment
- Moments.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Bending Moment (M)
Definition:
The moment that causes a beam to bend, dependent on load and location.
-
Term: Bending Stiffness (EI)
Definition:
A measure of a beam's resistance to bending, calculated as the product of the modulus of elasticity (E) and the moment of inertia (I).
-
Term: Curvature (κ)
Definition:
A measure of the bending of a curve, defined as the reciprocal of the radius of curvature.
-
Term: Axial Displacement
Definition:
The movement of points along the length of a beam under load, considered negligible in Euler-Bernoulli beam theory.