Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Stress Variation
Unlock Audio Lesson
Let's start with an essential concept: how does stress vary within a body under load? Stress is not uniform; it can differ points to point depending on the applied loads!
Could you explain why knowing stress at different points is crucial?
Great question, Student_1! Higher stress levels can increase the likelihood of failure, so we need to assess the distribution to predict behavior accurately.
How do we actually measure or calculate this variation?
We use stress equilibrium equations, which we'll derive in this lecture.
Linear Momentum Balance
Unlock Audio Lesson
Next, let's delve into the linear momentum balance. Imagine a small cuboid within our material — it helps us understand force interactions.
How does Newton's second law apply to this cuboid?
Exactly, Student_3! By applying Newton's second law, we can assess the net force acting upon the cuboid, considering traction on its surfaces.
What kind of forces are we talking about here?
Good question, Student_4! We're looking at internal tractions and body forces — both critical to understanding the material's response.
Traction Contributions
Unlock Audio Lesson
Let's focus now on traction contributions. Each face of our cuboid experiences forces due to the stress acting on it.
How do we represent this mathematically?
Great inquiry! We use a stress tensor to express these contributions mathematically, simplifying our equations.
Why do we need to use Taylor's expansion here?
Excellent point! Taylor's expansion helps us approximate stress variations across the cuboid's area, leading to accurate force calculations.
Conclusion of Stress Equilibrium Concept
Unlock Audio Lesson
To wrap up, understanding stress equilibrium equations is essential for predicting material failure.
So, understanding how stresses balance helps us innovate better materials!
Exactly, Student_3! Balancing forces leads to better designs in engineering applications.
I get it now, this knowledge can help prevent failures in real-world situations!
Precisely! Remembering these concepts is crucial as we move deeper into solid mechanics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces the stress equilibrium equations, highlighting how stress can vary within a body under load. Specifically, it outlines the need to determine stress levels at different points to predict failure chances, setting the stage for a deeper exploration of linear momentum balance and torque in solid mechanics.
Detailed
Introduction to Stress Equilibrium Equations
In solid mechanics, particularly when studying how materials respond to applied loads, understanding the variation of stress within a body is crucial. This section introduces the concept of stress equilibrium equations, emphasizing that
stress levels at various points can influence the overall behavior and failure of the body under load. The goal is to derive these equations to analyze how stresses are distributed within a material, which is fundamental for engineers and scientists in predicting material failure.
By applying Newton’s second law to a small cuboid within a material, we can explore the forces acting on it due to internal tractions and external body forces, leading to a comprehensive understanding of force balance and momentum changes within the material.
Youtube Videos
![Mechanics of Solids [Intro Video]](https://img.youtube.com/vi/TdmQGMUbUVw/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of the Body and Stress Variation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
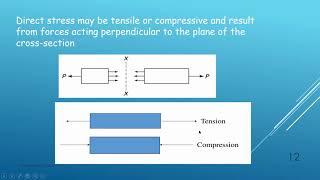
Let us suppose we have a body which could be clamped at some part of the boundary as shown in Figure 1. We have talked about traction and stress at a point but not about how stress is varying in the body.
Detailed Explanation
In this chunk, we're introducing the concept of a physical body that is fixed or clamped at some boundary. This setup is commonly encountered in mechanical systems where parts need to be held in place. The focus here is on understanding how stress, which is internal pressure in the material, varies throughout the body, rather than just at a single point. This variability is important because it helps us understand the performance and failure points of the body under load.
Examples & Analogies
Imagine a sponge being squeezed by two hands. While you can identify points where the pressure is high (like where you're squeezing it the hardest), the pressure differs across the entire sponge. Similarly, stress varies across different points in a mechanically restrained body.
Importance of Determining Stress Distribution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As we apply a load at some part of the boundary, the stress would be different at different points within the body. To decide where the body is going to fail, we need to know the value of stress at every point in the body. Higher the stress, more the chance of failure.
Detailed Explanation
This chunk highlights the crucial link between applied loads and stress distribution within a body. When a load is applied, each point in the material experiences different levels of stress based on its location, the material properties, and the boundary conditions. Understanding these differences is vital in engineering and materials science because high stress in certain areas can lead to failure, such as cracks or fractures. Therefore, we must measure or calculate stress throughout the entire body to prevent disasters in structural applications.
Examples & Analogies
Consider a suspended bridge; if you know different stress levels along its beams, you can predict when and where repairs are necessary, just like a doctor checks different body parts to assess health and prevent injury.
Role of Stress Equilibrium Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The stress equilibrium equations allow us to obtain the distribution of stress in a body.
Detailed Explanation
In this last chunk of the introduction, we introduce stress equilibrium equations as fundamental tools used in mechanics to derive stress distributions within a solid body under external loads. These equations are based on the principles of equilibrium, which state that for any piece of a material to remain stable, the internal stresses must balance out the applied external forces and moments. By solving these equations, engineers can predict how a component will behave under specified loads, which is crucial for safe and effective design.
Examples & Analogies
Think of stress equilibrium equations like balancing scales at a market. If you add weights to one side and don't balance it, one side tips over, leading to failure. Similarly, if stress is not balanced throughout a structure, it can lead to collapses or failures.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Stress Distribution: Refers to how stress is spread out over a material when it's subjected to forces.
-
Equilibrium Conditions: Conditions that must be satisfied for a body to be in a stable state under applied forces.
-
Traction Forces: Forces that arise at internal surfaces of a body due to stress, governing the internal force distribution.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: A steel beam under load will have higher stress concentration near its supports compared to the center of the span.
-
Example 2: When a person steps onto a soft surface, the stress experienced on the ground beneath their foot varies based on the weight and surface area contact.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Stress is not at rest, understand the test, the load is best!
📖 Fascinating Stories
-
Once a beam under a load learned how stress varied, it saved the city from collapse by understanding team effort!
🧠 Other Memory Gems
-
STRESS: Stress Transmission Relies on Equilibrium and Surface Support.
🎯 Super Acronyms
LMB
- Linear Momentum Balance - essential for deriving stress distributions.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Stress
Definition:
The internal force per unit area within materials that arises from externally applied forces, uneven heating, or permanent deformation.
-
Term: Equilibrium
Definition:
A state where forces acting on a body are balanced, resulting in no net force or moment.
-
Term: Traction
Definition:
The forces acting at the surface of a body that results from stress, influencing how loads are transmitted through materials.
-
Term: Linear Momentum
Definition:
A measure of the motion of a body, calculated as the product of its mass and velocity, which is important for understanding motion under forces.
-
Term: Body Force
Definition:
A force that acts throughout the volume of a material due to effects like gravity or electromagnetic fields.