Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Stress-Strain Relation
Unlock Audio Lesson
Today, we're beginning our discussion on the stress-strain relation. Can anyone tell me why it's essential to understand how stress and strain are related in materials?
It's important because we need to know how much stress a material can handle without breaking.
Exactly! Understanding this relation helps ensure that materials stay within safe limits. Remember, we often call this the constitutive relation, focusing on how materials respond to external loads.
So, if we understand the relationship, we can predict failure points in materials?
Absolutely! Predicting failure is critical in engineering. What happens if we don’t have this relation?
We might not be able to analyze material behavior accurately, leading to potential disasters.
Right! It could lead to catastrophic failures in structures. Let's delve deeper into how we can derive this stress-strain relationship from equilibrium equations.
Equilibrium Equations and Unknowns
Unlock Audio Lesson
When we set up our equilibrium equations, typically we deal with three equations and multiple unknowns. How many stress components can we encounter?
We can have nine components in total, right?
Correct! But due to the symmetry in stress tensors, we actually only have six independent components to worry about. Can anyone tell me what this implies?
It means we have more unknowns than equations, which makes solving them difficult!
Yes! This is where the stress-strain relation becomes essential. It provides the additional equations we need to solve these systems. Let's discuss how displacement and strain relate to stress.
So, we can express strain in terms of displacement?
Exactly! And through this connection, we can indirectly express stress in terms of displacement as well. Let's learn how that works.
Lagrangian Description of Motion
Unlock Audio Lesson
In the study of motion under deformation, we often refer to the Lagrangian description. What do you think this implies?
Does it mean we track the movement of particles based on their positions in the reference configuration?
Exactly! By keeping a reference point, we can derive useful equations for velocity and acceleration. Why is this approach useful for our understanding?
It helps us find out how stresses develop as the material deforms, right?
Correct! And we've now established how stress relates to strain, helping us solve complex mechanical problems effectively.
Could we consider both linear and nonlinear stress-strain relationships?
Yes! Most initial analyses use linear relationships for simplicity, but we will also explore nonlinear scenarios in the future.
Constitutive Relations
Unlock Audio Lesson
Let's summarize our understanding so far. Anything important we’ve discussed about stress-strain relations?
The constitutive relation helps us connect stress and strain and is vital in predicting material behavior.
Yes! Remember, these relations help solve for the stresses in various loading conditions, which is crucial in structural engineering.
And understanding these relations helps avoid engineering failures, right?
Absolutely! It's a foundation for ensuring the safety and stability of structures. Keep this principle in mind as we move into more complex models in future lessons.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section elaborates on the importance of the stress-strain relation in solid mechanics, emphasizing that understanding stress is crucial for preventing material failure. It explains how these relationships allow for the interpretation of equilibrium equations and the behavior of materials under loads, leading to accurate predictions of deformation and stress distribution.
Detailed
Detailed Summary
In this section, we explore the fundamental need for the stress-strain relation in solid mechanics. The behavior of materials when subjected to external loads is analyzed by considering a body fixed at one boundary and subjected to an external force at another. The initial state of a material is characterized by its reference configuration, represented by a position vector X, which displaces to x due to deformation.
Understanding stress is essential to ensure that the material operates within safety limits to avoid failure or fracture. The equilibrium equations established are foundational in determining internal stresses within materials but pose a challenge due to the number of unknowns and the limited number of equations available. This section outlines how the stress-strain relationship acts as a crucial bridge, enabling us to express stress in terms of strain, thus linking these concepts and allowing for a comprehensive understanding of material deformation.
Key aspects discussed in this section include:
- The equations of equilibrium and the inherent challenges of solving them without additional information about stress.
- The significance of the stress-strain relation, also known as the constitutive relation, to derive stress from displacement.
- The understanding of velocity and acceleration in a Lagrangian framework, considering time derivatives during deformation.
Establishing this relationship is pivotal in progressing to solutions of the deformed body, facilitating advancements in safety and design in engineering applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Stress and Strain Relationship
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
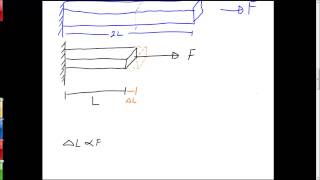
Consider a body clamped at one part of the boundary and acted upon by an external load on another part of its boundary as shown in Figure 1. Any general point in the reference configuration (denoted by position vector X) is displaced by u(X,t) as shown in the figure.
Detailed Explanation
A body experiences changes when forces are applied to it. When part of a body is fixed, and the other part is loaded, the body deforms, meaning its shape changes. The position of a point in the original shape of the body, denoted as 'X', shifts to a new position given by 'u(X,t)', which shows how much it moves and how time affects this movement. This relationship is crucial for understanding how materials respond to forces.
Examples & Analogies
Think of a rubber band. When you pull one end while the other is held tight, it stretches and deforms. The point where you measure the rubber band’s stretch from is similar to 'X', and how much it stretches away from that point is comparable to 'u(X,t)'.
Importance of Stress in Material Strength
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Usually, we are interested in knowing the final deformed shape of the body and the stress generated in it. The knowledge of stress is important because it helps us to check if it is within the prescribed limits so that the body does not fail or fracture.
Detailed Explanation
Understanding stress is crucial because it informs us whether the material can handle the applied forces without breaking. Engineers and designers need to ensure that the stress does not exceed certain limits; otherwise, the material might fail or fracture. This concept is essential for safety in buildings, bridges, and other infrastructures.
Examples & Analogies
Consider a bridge: engineers must calculate the stress on different parts of the bridge to ensure it can safely support traffic. If the stress exceeds limits, it could lead to the bridge collapsing, much like how a weight placed too heavily on a thin shelf could cause it to snap.
Equilibrium and Stress Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In order to find stress in the body, we can use the following equations of equilibrium derived earlier. We have nine unknown components of stress matrix in three equations here. Using symmetry of stress matrix, the number of unknowns reduces to six.
Detailed Explanation
To analyze the stress within a body, we apply equilibrium equations which consider the balance of forces. Initially, there are nine unknown components of stress that we must solve, but using the symmetrical properties of the stress matrix, we simplify this to six unknowns. This mathematical reduction is key for solving real-world problems efficiently.
Examples & Analogies
Imagine trying to balance a book on your head. You might initially think about how much pressure is on each corner of the book. By recognizing the symmetry (the book is balanced evenly), you can reduce the complexity of your calculations and focus on just a few points while maintaining balance.
Need for Additional Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus, this system cannot be solved without the help of additional equations. These additional equations are given by stress-strain relation.
Detailed Explanation
When we set up the equations to solve for stress using equilibrium, we find that we have more unknowns than equations. To resolve this issue, we require additional relationships known as stress-strain relations to link stress and strain directly, allowing us to express one in terms of the other.
Examples & Analogies
Think of a puzzle: if you have more pieces than the slots available, you need additional rules or information about how the pieces fit together. Similarly, the stress-strain relationship provides the necessary connections to solve the mathematical puzzles in structural analysis.
Expressing Stress in Terms of Strain
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If we can now in some way express stress in terms of strain, then indirectly, we have actually expressed stress in terms of displacement.
Detailed Explanation
By deriving a relationship between stress (the internal forces) and strain (the deformations), we simplify our equations to handle just the displacements of the body. This transformation makes it easier to analyze how a material will respond under load, paving the way to solve the equilibrium equations.
Examples & Analogies
Imagine a sponge. When you press it (apply stress), it deforms (strain). By knowing how much it squishes for a given pressure, you can predict how much it will squish under different pressures, allowing you to design things like sponges for specific uses based on their stress-strain characteristics.
Constitutive Relation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus, the stress-strain relation is necessary to get the deformed solution of a body from equilibrium equations. Often, the stress-strain relation is also called constitutive relation.
Detailed Explanation
The relationship between stress and strain is pivotal in material science and solid mechanics because it allows engineers to predict how materials will behave under various loading conditions. It’s one of the fundamental principles that guide the design of safe and effective materials and structures.
Examples & Analogies
Think of a tuning fork. When you strike it, it vibrates. The stress and strain relationship illustrates how the material responds to being struck, and engineers use this principle to understand how materials can vibrate in musical instruments, which is vital for creating the right sounds.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Stress: The internal force per unit area within materials that resists deformation.
-
Strain: The change in shape or dimensions of a material due to applied stress.
-
Equilibrium equations: Mathematical formulations that express the balance of forces in a material.
-
Constitutive relation: The mathematical expression linking stress and strain.
-
Lagrangian description: A method of describing motion relative to an object's initial configuration.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A steel beam subjected to a load will deform, exhibiting both stress and strain. By analyzing these, engineers can predict whether the beam will fail under specified loads.
-
In a rubber band, stretching it leads to a specific strain that can be quantitatively related to the stress applied, showcasing the stress-strain relation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Stress and strain in the skeletal frame; keep them in check to avoid any blame.
📖 Fascinating Stories
-
Imagine a bridge made of steel that bends slightly under heavy traffic. This bending is stress and strain working together, and knowing their relationship prevents catastrophic failure.
🧠 Other Memory Gems
-
S.S. = Safety Secured through Stress-Strain knowledge.
🎯 Super Acronyms
SOS
- Stress Overcomes Safety - remember to analyze stress-strain relations to ensure safety.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Stress
Definition:
The internal resistance of a material to deformation, typically expressed as force per unit area.
-
Term: Strain
Definition:
The measure of deformation representing the displacement between particles in a material.
-
Term: Constitutive Relation
Definition:
An equation that relates stress and strain, essential for predicting material behavior.
-
Term: Equilibrium Equation
Definition:
A mathematical statement that expresses the balance of forces acting on a body.
-
Term: Lagrangian Description
Definition:
A formulation in mechanics that describes motion based on the positions of particles in their reference configuration.