Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Stress and Strain Tensors
Unlock Audio Lesson
Welcome, class! Today, we'll start by discussing the stress and strain tensors, which are vital concepts in solid mechanics. Can anyone tell me what a stress tensor represents?
Isn't it about the internal forces acting within a material?
Exactly! And similarly, the strain tensor measures how much a material deforms under those stresses. Both tensors have mathematical similarities. For instance, both contain normal and shear components. Why do you think this similarity is important?
It might help in applying the same principles we learned in stress analysis to strain analysis?
Right! Knowing their parallels can simplify our work with these concepts.
Principal Components of Strain and Stress
Unlock Audio Lesson
Let’s talk about principal directions. Can anyone explain what principal stresses are?
I think they are the directions where the stresses are maximized or minimized.
Correct! And similarly, we can have principal strain directions. The maximum longitudinal strains occur in those principal directions. How do we mathematically find these directions?
By finding the eigenvectors of the strain tensor?
Yes! That's an important connection. The eigenvalues give us the principal strain components.
Mohr's Circle for Strain
Unlock Audio Lesson
Now let's explore Mohr’s circle for strain. Do you remember how we used it for stress?
Yes, it helped visualize the normal and shear stresses on different planes.
Exactly! We can do something similar for strain. How does the positioning of axes change in a strain circle compared to a stress circle?
I think the vertical axis has an extra factor of 2 for shear strain because of its formula?
Great observation! This adjustment allows us to derive the maximum shear strain from the radius of the circle.
Decomposition and Invariants
Unlock Audio Lesson
Let’s move on to the decomposition of tensors. What are the two components we can divide them into?
Hydrostatic and deviatoric components?
Correct! The volumetric strain tensor corresponds to the hydrostatic part. What do our invariants help us understand?
They provide fundamental properties that don't change with coordinate transformations.
Precisely! They give us vital characteristics of the material, regardless of how we view it.
Strain Compatibility Conditions
Unlock Audio Lesson
Lastly, let’s cover strain compatibility conditions. Why do we need to enforce these conditions?
To ensure that our strain functions produce a valid displacement function?
Exactly! Without these constraints, we can end up with overlapping or impossible physical displacements. Can you think of an example of where this might occur?
Maybe in situations with large deformations?
That’s a good point! Always remember to check compatibility in your analyses.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section outlines how stress and strain tensors share analogous properties, particularly their symmetric nature and principal components. It discusses practical applications such as Mohr's circle for strain, strain compatibility conditions, and showcases examples that demonstrate these concepts.
Detailed
Similarity Between Stress and Strain Tensors
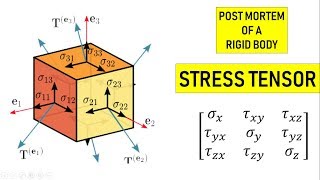
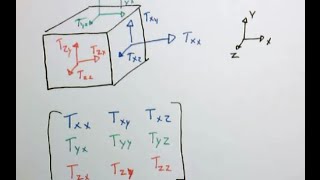
In this section, we delve into the similarities between stress and strain tensors in mechanics. Both tensors are fundamental to understanding material deformation and stress response within solid mechanics. Stress tensors, denoted with sigma (σ), represent the internal forces experienced by a material, while strain tensors, denoted with epsilon (ϵ), quantify deformation. Below are some key points discussed:
Key Points:
- Mathematical Similarity: Both tensors possess similar mathematical structures; their normal components and shear components follow analogous formulations.
- Principal Directions: Just as with stress, we can define principal directions and components for strain, where the maximum/minimum values of strains occur along specific line elements.
- Diagonal Representation: In their principal coordinates, both stress and strain tensors exhibit diagonal forms, simplifying calculations and interpretations of physical effects.
- Maximum Shear Strain: Like stress, the maximum shear strain can also be derived from principal strains demonstrated through geometrical considerations such as angles between line elements.
- Mohr’s Circle for Strain: Similar to Mohr's circle for stress, this tool is adapted for strain, allowing visual interpretation of shear strains and longitudinal strains.
- Invariants and Decomposition: The invariants of strain tensors parallel those of stress tensors, facilitating deeper understanding and formulation of tensor decomposition into volumetric and deviatoric parts.
- Strain Compatibility: Strain compatibility conditions are critical, emphasizing that any combination of strain must lead to a consistent displacement function without overlaps in the material.
Overall, recognizing these similarities aids in applying stress concepts to strain analysis effectively.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Stress and Strain Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us list the formulae of stress and strain components derived earlier to observe the similarities between the two. On the stress side, we have normal (σ) and shear (τ) components of traction while on the strain side, we have longitudinal (ϵ) and shear (γ) strains as shown below. We can notice the similarity in above formulas.
Detailed Explanation
In mechanics, stress and strain are two fundamental concepts that describe the behavior of materials. Stress (σ) is the force applied per unit area, while strain (ϵ) is a measure of deformation representing the displacement between particles in a material body. Both stress and strain have normal and shear components, which make up their respective tensor forms. These components indicate how the material will behave when subjected to forces, and observing their formulas reveals a close resemblance between the two, allowing us to apply principles of stress analysis directly to strain analysis.
Examples & Analogies
Think of stress like the pressure you feel when someone pushes on your arm, and strain as the actual deformation of your arm during that push. Just as we can measure how much pressure we apply (stress), we can measure how much your arm bends or stretches (strain), and the formulas for these measurements look quite similar.
Principal Directions and Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We can also define principal strain directions (not planes) and principal strain components. We know that at a point, principal stress planes are the planes on which the normal component of traction is maximized/minimized. Similarly, at a point in the body, out of the numerous line elements, the directions of those line elements that experience maximum/minimum longitudinal strain are called principal strain directions.
Detailed Explanation
Principal strains are the normal strains that occur when the material is oriented at a specific angle. Just like principal stress planes, where the stress reaches maximum or minimum values, principal strain directions indicate where the strain is maximized or minimized. To identify these directions, we utilize mathematical techniques like finding eigenvectors of the strain tensor. This means that the material has specific orientations where it elongates or compresses the most when forces are applied.
Examples & Analogies
Imagine stretching a rubber band. There are specific angles at which the rubber band stretches the most. Finding these angles is similar to finding the principal strain directions, where the strains are at their highest when you apply the force in certain directions.
Diagonality of Matrix in Principal Coordinate System
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When we represent the strain matrix in the coordinates system of the principal strain directions, it will become a diagonal matrix. The off-diagonal components will be zero, which means that if we take the two line elements directed along the principal strain directions, there will not be any change of angle between them.
Detailed Explanation
In the principal coordinate system, the strain matrix takes a simplified form—diagonal. This means that the associated strains in the specific directions do not interact, leading to no shear strains acting on those axes. It is a powerful visualization tool that denotes clear relationships between various components without angular distortion.
Examples & Analogies
Think of a photo of a rectangular object. If you capture it in the right perspective (principal coordinates), it appears exactly rectangular without any distortion. When the object is aligned with the camera, you see clear corners without skew; similarly, a diagonal strain matrix indicates clean, straightforward relationships between strain components.
Maximum Shear Strain
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We can also maximize shear strain at a point just like we maximized the shear component of traction. The pair of perpendicular line elements that undergo maximum change in angle will be directed at 45° from principal strain directions.
Detailed Explanation
Just as we can determine where shear stress is maximized by looking at certain angles, the same applies to shear strain. The maximum shear strain happens at 45 degrees to the principal strain directions, which signifies a critical orientation when analyzing material deformation.
Examples & Analogies
Think of twisting a piece of dough. At certain angles, you’ll feel it stretch easier; similarly, shear strain that has maximum impact will occur at these angles. When you find the right twist, it starts to bulge out more!
Mohr's Circle for Strain
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We can also think of Mohr’s circle for strain. If we know the value of longitudinal strain along two perpendicular directions and also know shear strain between them, we can use Mohr’s circle for strain to obtain longitudinal and shear strains for two perpendicular line elements oriented at an angle θ.
Detailed Explanation
Mohr's Circle is a graphical representation that helps visualize the relationships between normal and shear strains. It allows us to extract crucial information about how strains interact based on their orientations. Using the circle, we can find the resultant strains, which makes it easier to understand complex strain situations without delving into complicated matrices.
Examples & Analogies
Imagine a pie chart; each slice represents different strains at various angles. By knowing two parts of the pie (two strains), we can easily find the rest using the relationships illustrated by the circle. It simplifies what could otherwise be a convoluted analysis.
Invariants of Strain Tensor
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Just like we have invariants of the stress tensor as I1, I2, and I3, we also have invariants of the strain tensor denoted by J1, J2, and J3.
Detailed Explanation
Invariants are quantities derived from the tensors (stress or strain) that remain unchanged under any transformation (like rotation or translation). The invariants provide important information about the overall state of the material without being affected by its orientation, allowing for a deeper insight into the material's behavior.
Examples & Analogies
Think of invariants as the core characteristics of a person. No matter how their appearance changes (like dressing differently or changing hairstyles), their qualities (like kindness, intelligence, or skill) remain unchanged. Similarly, strain tensor invariants give us the fundamental properties of strain independent of orientation.
Decomposition of the Strain Tensor
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We can also decompose the strain tensor into two parts. The first part is proportional to identity and is called the volumetric strain tensor. The second part is called the strain deviator, responsible for distorting the body.
Detailed Explanation
The decomposition helps in analyzing the overall behavior of materials under stress. The volumetric part affects the volume change (not shape) while the deviatoric part contributes to shape distortion. This breakdown allows for targeted analysis, distinguishing between these two aspects.
Examples & Analogies
Think about inflating a balloon. When you pump air into it, the volume increases (volumetric strain), but its shape also changes to a more spherical form (strain deviator). Understanding these two aspects separately can help in predicting how the balloon will behave when filled.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Stress Tensor: Represents internal forces within a material.
-
Strain Tensor: Quantifies deformation due to stress.
-
Principal Directions: Maximum/minimum directions for stress or strain.
-
Mohr's Circle: Graphical tool for analyzing stresses and strains.
-
Invariants: Unchanging properties of tensors under transformations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a beam subjected to bending, the stress tensor can illustrate the internal forces as a function of distance from the neutral axis.
-
Mohr’s Circle for strain can show how the maximum shear strain occurs at a 45-degree angle to the principal strain directions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Stress makes us tense, it shows internal force, while strain is the change, in shape, of course!
📖 Fascinating Stories
-
Imagine a rubber band, stretching and snapping back; stress pulls it tight, strain shows the slack. Together they dance on the mechanics track!
🧠 Other Memory Gems
-
For remembering Mohr's Circle, think 'Max and Shear - angle in gear!'
🎯 Super Acronyms
PES = Principal, Eigenvalues, Strain – remember to keep track!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Stress Tensor
Definition:
A mathematical representation that describes the internal forces experienced by a material.
-
Term: Strain Tensor
Definition:
A mathematical representation that quantifies how much a material deforms under stress.
-
Term: Principal Directions
Definition:
Directions along which stress or strain reaches a maximum or minimum value.
-
Term: Mohr's Circle
Definition:
A graphical representation used to determine stress or strain components on different planes.
-
Term: Eigenvalues
Definition:
Values that determine the principal components of a tensor through its characteristic equation.
-
Term: Invariants
Definition:
Quantities derived from tensors that remain unchanged under coordinate transformations.
-
Term: Deviatoric Component
Definition:
The part of the tensor responsible for changes in shape without affecting volume.
-
Term: Hydrostatic Component
Definition:
The part of the tensor that causes a uniform change in volume without altering shape.
-
Term: Strain Compatibility Conditions
Definition:
Conditions that ensure displacements derived from strain tensors do not lead to overlaps or inconsistencies.