Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Strain Tensor
Unlock Audio Lesson
Today, we'll discuss the strain tensor and its representation in cylindrical coordinates. Can anyone explain what the strain tensor represents?
Isn't it a measure of deformation in materials?
Exactly! The strain tensor reflects how much an object deforms. Let's dive into how this tensor is structured in cylindrical coordinates, starting with the gradient of displacement.
Gradient Representation in Cylindrical Coordinates
Unlock Audio Lesson
In Cartesian coordinates, the gradient of a quantity is straightforward. However, in cylindrical coordinates, the gradient is adjusted for the circular nature of the system, specifically by dividing the derivative with respect to θ by r. Why do you think that's necessary?
This adjustment accounts for the radial distance in cylindrical coordinates!
Right! This ensures we're accurately measuring the change in displacement across our coordinates. Let’s look at how we express the displacement vector next.
Displacement Vector in Cylindrical Coordinates
Unlock Audio Lesson
The displacement vector can be decomposed into three components: radial, circumferential, and axial. Can anyone name them?
u_r, u_θ, and u_z!
Great memory! As we visualize this in a cylindrical body, it's important to understand how these components contribute to the strain matrix. Let's move on to derive the displacement gradient.
Derivation of the Strain Matrix
Unlock Audio Lesson
Using the displacement gradient, we can find the strain matrix as the symmetric part. What gives rise to these additional terms in cylindrical coordinates?
The changing basis vectors as you move around the axis, right?
Absolutely! These terms reflect the uniqueness of cylindrical systems. Lastly, let’s examine the physical significance of each strain component.
Significance of Strain Components
Unlock Audio Lesson
Now that we've derived the strain matrix, how do these components, like ε_rr and ε_θθ, relate to the physical shape of the object?
They describe how the object stretches in the radial and circumferential directions!
Correct! Stress and strain can be directly correlated, especially in isotropic materials. Each component plays a role in determining how materials respond under load.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we derive the strain tensor and its matrix representation in cylindrical coordinates, building from gradient and displacement definitions and examining the significance of strain components. Emphasis is placed on the relationship between stress and strain within isotropic materials.
Detailed
In this section, we delve into the representation of the strain tensor in cylindrical coordinate systems, building upon prior lectures discussing equilibrium equations. We begin with a review of the strain tensor's definition and its matrix form in Cartesian coordinates. Next, we express gradients and displacement vectors in cylindrical coordinates. The importance of understanding displacement gradients leads us to derive the displacement gradient matrix. Subsequently, we derive the strain matrix as the symmetric part of this gradient, detailing each strain component's physical significance. Further, we explore the relationship between stress and strain for isotropic materials, highlighting how to relate the two matrices regardless of coordinate system. This section emphasizes essential concepts and their implications in solid mechanics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Strain Tensor
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The strain tensor (ϵ) is defined as (1) Wecan recallits matrix form in Cartesian coordinate system: (2)
Detailed Explanation
The strain tensor ϵ represents the deformation of a material. It is a mathematical object that relates the change in shape or size of an object to the forces acting on it. In this context, we first need to understand its representation in Cartesian coordinates, which serves as a foundation before we can translate this representation into cylindrical coordinates.
Examples & Analogies
Imagine a rubber band being stretched. The strain tensor would help describe how the rubber band stretches in various directions as you pull on it.
Gradients in Cylindrical Coordinates
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
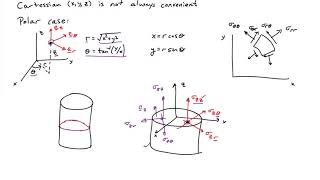
We need to first express gradients in the cylindrical coordinate system. In Cartesian coordinate system, the gradient of a quantity is given by (3) whereas its definition in cylindrical coordinate system is (4). Notice that the partial derivative with respect to θ is divided by r as θ is non-dimensional and we are taking the gradient in space.
Detailed Explanation
In the cylindrical coordinate system, gradients must be expressed differently than in Cartesian coordinates. The gradient helps to describe how a quantity changes in space. Specifically, in cylindrical coordinates, the partial derivative with respect to the angle θ is adjusted because this angle is a non-dimensional measure. This change allows us to correctly capture how changes in displacement occur within the cylindrical framework.
Examples & Analogies
Think of standing in the center of a circular field. If you observe changes in how high grass grows at different angles from your position, the gradient helps you understand how that growth varies around you, accounting for the circular nature of your surroundings.
Displacement Representation in Cylindrical Coordinates
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The displacement vector can be written in cylindrical coordinate system by decomposing it along cylindrical basis as follows: u = u_e + u_e + u_e (5) r r θ θ z z
Detailed Explanation
The displacement vector, which describes how a point moves in space, can be represented in cylindrical coordinates by breaking it down into components along the radial (r), angular (θ), and axial (z) directions. Each of these components represents how much the displacement occurs in each respective direction, giving a complete picture of the object's deformation.
Examples & Analogies
Imagine a balloon being inflated. The displacement vector helps you understand how the surface of the balloon stretches in three different directions: outward (radial), around the balloon (angular), and along the height (axial) as it expands.
Displacement Gradient Representation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, we can plug in the displacement vector given in equation (5) in the gradient definition (4) to obtain (6). For the terms here, the basis vectors act as a constant as they change only with θ.
Detailed Explanation
By substituting the displacement vector into the gradient definition, we compute the gradient of the displacement, which captures how the displacement varies in space. We also observe that some aspects of the basis vectors remain constant except when changing direction around the cylindrical body.
Examples & Analogies
Think of a hill. As you walk on the hill, certain aspects of the landscape (like the steepness in a particular direction) change while others may remain flat. The calculation described allows us to understand those changes in displacement over the landscape, capturing the 'gradient' of your movement.
Strain Tensor Representation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, we can use equation (1) to obtain strain matrix which is the symmetric part of the displacement gradient matrix derived above. It turns out to be the following: (10)
Detailed Explanation
The strain matrix is derived as the symmetric part of the displacement gradient matrix. The symmetric nature means it effectively captures how the material deforms under stress without redundantly incorporating rotational effects. Understanding this matrix is crucial for relating deformation to applied forces on the cylindrical body.
Examples & Analogies
Think of a sponge. When you squeeze it, the way it compresses and expands represents its strain. The strain matrix allows us to quantify how each part of the sponge reacts differently when pressured, ignoring any twisting.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Strain Tensor: Represents the deformation of materials.
-
Cylindrical Coordinates: Essential for analyzing structures like pipes or cylindrical shells.
-
Gradient in Cylindrical Coordinates: Adjusts physical measurement for curvature.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of a hollow cylinder that experiences radial strain during expansion.
-
Example of how hoop strain affects the durability of gas pipelines.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Cylinders bend and twist, strain's what we can't miss.
📖 Fascinating Stories
-
Imagine a balloon inflating; it expands in all directions, like the radial and hoop strains.
🧠 Other Memory Gems
-
Remember 'R.H.Z.' for Radial, Hoop, and Z-axes in cylindrical coordinates.
🎯 Super Acronyms
STR (Strain, Tensor, Representation) for strain's fundamental concepts.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Strain Tensor
Definition:
A mathematical representation of deformation in a material, represented as a matrix.
-
Term: Displacement Vector
Definition:
A vector that describes the change in position of points in a given material.
-
Term: Gradient
Definition:
A mathematical operation that represents the rate of change of a quantity.
-
Term: Cylindrical Coordinates
Definition:
A three-dimensional coordinate system defined by a radial distance, angle, and height.
-
Term: Isotropic Material
Definition:
A material whose properties are the same in all directions.
-
Term: Hoop Strain
Definition:
Strain occurring in the circumferential direction of a cylindrical object.