Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Stress Matrix
Unlock Audio Lesson
Welcome everyone! Today we are discussing the concept of the stress matrix, which is vital in solid mechanics. Can anyone tell me what a stress tensor is?
Isn't it a mathematical representation of stress at a point?
That's correct! The stress tensor encapsulates various stress components at a point in a material. The stress matrix represents this tensor in a particular coordinate system. Can anyone tell me why we need to transform the stress matrix to different coordinate systems?
To analyze different orientations of structures, right?
Exactly! The transformation allows us to understand how stress states appear from various perspectives. Remember, while the stress matrix changes, the physical stress tensor remains constant. That's an important point to remember!
Transformation of Stress Matrix
Unlock Audio Lesson
Now, let's move on to the transformation of the stress matrix. How do we relate stress matrices in different coordinate systems?
We use a rotation tensor, right?
Correct! The rotation tensor helps relate one set of basis vectors to another. So, if we have our stress matrix from one coordinate system, we can find a new matrix using this tensor. Can anyone remind us of the notation used for this transformation?
It’s sigma and the hat notation, right?
Great recall! We denote transformed components using different symbols, which helps distinguish between original and transformed values. It's crucial for clarity when applying the formulas.
Application of the Transformation
Unlock Audio Lesson
Let’s consider applying these transformations in a practical example. When using rotation matrices, how do we compute them?
We derive them based on the angle of rotation, correct?
Exactly! For instance, a rotation matrix for a 45-degree angle would look different from that of a 90-degree angle. How do these matrices impact the stress matrix formulation?
They help us find the new stress matrix representation?
Yes! After finding the rotation matrix, we apply it to transform the stress matrix accordingly. Let’s verify the transformation by calculating traction on a specified plane using our derived matrix.
Verification of Stress Matrix
Unlock Audio Lesson
To verify our stress matrix, we can calculate the traction on a specific plane. Who remembers the formula we discussed for traction?
It's based on the stress matrix and the normal vector, right?
Correct! The traction on a plane normal to the vector involves multiplying the stress matrix by this vector. Let’s see an example and how to confirm our results.
What if the results differ? How should we handle that?
Good question! If results differ, we need to double-check calculations and ensure our normal vectors and transformation processes were correctly applied.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses the stress matrix, its formation from traction vectors in a coordinate system and its transformation when changing coordinate systems. The relationship between the stress matrix and rotation tensors is highlighted, showcasing the preservation of the stress tensor despite changes in representation.
Detailed
Detailed Summary
The stress matrix represents the stress tensor in a given coordinate system and plays a crucial role in mechanics. It can change when we transition from one coordinate system to another, although the stress tensor itself remains unaffected. To construct the stress matrix from a stress tensor, we select a coordinate system (e1, e2, e3) and determine the traction forces acting on planes whose normal vectors align with these basis vectors. In a different coordinate system, we repeat the process using the new basis vectors.
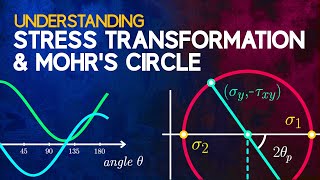
The transformation of a stress matrix involves establishing a relationship between stress matrices in distinct coordinate systems using a rotation tensor. By expressing the traction on an arbitrary plane, we facilitate the understanding of how stress components relate when coordinates change. The section elaborates on deriving transformation equations and illustrates using a practical example, where a rotation matrix derived from a specified angle modifies the stress representation. Verification methods using traction calculations reinforce the theoretical framework laid out, ensuring a comprehensive grasp of stress matrices.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Stress Matrix
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
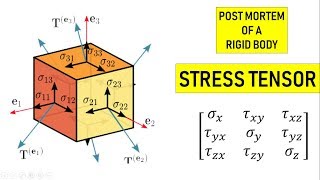
It is the representation (matrix form) of the stress tensor in a coordinate system. The stress matrix changes from one coordinate system to another but the stress tensor itself remains the same.
Detailed Explanation
A stress matrix is a mathematical representation of the internal forces (stresses) acting within a material or structure. When we change the coordinate system used to analyze these stresses, the representation of the stress in matrix form adjusts accordingly. However, the actual physical stress within the material remains constant, regardless of how we choose to analyze or represent it. This means the stress matrix is dependent on the coordinate system, but the underlying stress tensor (the physical reality) does not change.
Examples & Analogies
Imagine you're looking at a box from different angles. The way you describe what you see (the matrix representation) might change depending on your viewpoint (coordinate system), but the box itself (the stress tensor) remains unchanged.
Forming the Stress Matrix
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
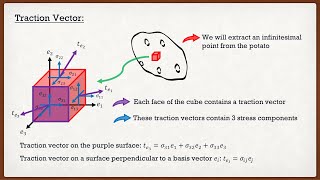
If we want to get the stress matrix of a stress tensor, then we first choose the coordinate system (let’s say e₁, e₂, e₃). We then find traction on the three planes whose normals are e₁, e₂, and e₃ and form columns out of those tractions.
Detailed Explanation
To create a stress matrix, the first step is selecting a coordinate system. After that, we identify forces acting on specific plane sections of the material. For each section (which corresponds to a normal vector in our chosen coordinate system), we calculate the stress (traction) acting on that section. These tractions become the columns of the stress matrix. So, if we have three planes corresponding to our three coordinate directions, we ultimately create a three-column matrix representing these tractions.
Examples & Analogies
Think about how you might build a report card for a student. You first decide on the subjects (coordinate system), then you collect grades for each subject (tractions on the planes), and finally you arrange these grades into a table (the stress matrix) that summarizes their performance.
Changing Coordinate Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In case we have a different coordinate system, we simply have to find traction on planes whose normals are the basis vectors of the new coordinate system and then form columns from these tractions.
Detailed Explanation
If we switch to a different coordinate system, the process of finding stress remains similar: we just need to compute the stresses (or tractions) on planes defined by the new set of basis vectors. By recalculating the stresses for these new planes, we can once again construct the stress matrix for the new coordinate system. This effectively shows how the stress matrix varies while the actual stress tensor remains constant.
Examples & Analogies
Returning to the box analogy, if you change the angle from which you're looking at the box, you will describe the dimensions and angles differently. But the box itself is unchanged. In the same way, how stresses are represented in a new frame changes, while the actual stresses active in the material do not.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Transformation of Stress Matrix: Refers to the process of relating stress matrices from different coordinate systems using rotation tensors.
-
Traction Vectors: Forces acting on specific planes in response to stress states, crucial for determining the stress matrix.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Given a stress matrix in e1, e2, e3 coordinates, derive the new stress matrix after rotating the coordinate system by 45 degrees.
-
Using the rotation matrix for a 60-degree turn, calculate the new stress tensor components.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Stress tensor stays the same, matrix transforms, that’s the game.
📖 Fascinating Stories
-
Imagine a stress tensor as a character traveling through various lands (coordinate systems), changing outfits (matrix forms) but keeping the same identity (stress state).
🧠 Other Memory Gems
-
S.T.R.E.S.S: Shift the Tensor in Relation to Every System Setup.
🎯 Super Acronyms
M.A.T.R.I.X
- Matrix And Tensor Representation In eXtraction.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Stress Matrix
Definition:
A representation of the stress tensor in a specific coordinate system.
-
Term: Stress Tensor
Definition:
A mathematical object defining the stress state at a point in a material.
-
Term: Rotation Tensor
Definition:
A mathematical representation that relates different coordinate systems through rotation.
-
Term: Traction
Definition:
The force per unit area acting on a specific plane within a material.