Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Traction Vector
Unlock Audio Lesson
Today, we’ll start with the concept of the traction vector. The traction vector describes how forces are acting on a given surface. Can anyone tell me why this might be important in solid mechanics?
I think it's important because it helps us understand how materials will respond under different loads.
Exactly! Now, when we calculate the traction vector at a point, we use a plane with a specific normal vector, right? This helps us define the direction and magnitude of the force.
Does that mean we can choose any plane we want?
Yes, and that's the interesting part: no matter which three planes we use, the resultant traction vector remains the same. This independence is crucial.
Let’s remember this with the acronym T.I.P: Traction Independence on Planes. Can we all repeat that?
T.I.P - Traction Independence on Planes.
Understanding the Stress Tensor
Unlock Audio Lesson
Great! Now that we’ve understood the traction vector, let’s move on to the stress tensor. Who can summarize how the stress tensor relates to the traction vector?
Isn’t it a way to express the traction vector for every possible plane at a point?
Spot on! The stress tensor encapsulates all of the traction vectors in a matrix form which allows us to represent how forces are distributed in multi-dimensional space.
So it’s like a summary of all tractions at a point?
Exactly! And it’s important because it helps us solve more complex problems in solid mechanics. Imagine trying to analyze a bridge's stress; without the stress tensor, it would be almost impossible.
Let’s use the mnemonic ‘STEM’ for Stress Tensor Equally Multiplies forces when transitioning from traction vectors.
STEM - Stress Tensor Equally Multiplies.
Practicing the Concepts
Unlock Audio Lesson
Now, I’d like you all to consider a cube of material. How can we visualize the stress tensor for this cube based on what we’ve learned?
We can think about the different faces of the cube and how traction vectors would act on them.
Correct! The traction forces would vary based on the planes. How do we justify that the stress tensor will work for any orientation?
Because the tensors themselves capture all possible interactions and tensions, it doesn’t matter how we rotate the cube.
Right! This versatility is what makes tensors so powerful in physical representations. Let’s summarize: in tensor notation, we can easily switch perspectives without losing meaning.
Remember this key idea with the mnemonic ‘TENSORS’: Tension Equivalents Navigate Stress and Orientation Responsively.
TENSORS - Tension Equivalents Navigate.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The traction vector is a fundamental concept in solid mechanics that describes the distribution of force on a surface. The section explains how to calculate the traction vector for any arbitrary plane and emphasizes that the calculated values remain consistent regardless of the planes chosen. Additionally, the section introduces the stress tensor, which is derived from the traction vector.
Detailed
Traction Vector
The traction vector is critical for understanding stress distribution within a material. It is defined at a point on any plane with a normal vector and can be calculated using different orientations of planes. Equation (2) highlights that the value of the traction vector remains invariant regardless of the choice of three planes used to derive it. The independence from the selection of these planes underlines the universality of the traction vector concept, making it reliable for further applications in stress analysis. Furthermore, this section leads into the definition of the stress tensor, which formalizes the relationship between traction and stress in a material, indicating how forces are transmitted through different cross-sections.
Key Points
- Definition and calculation of the traction vector on arbitrary planes.
- The consistency of the traction vector indicating its independence of a particular plane orientation.
- Introduction of the stress tensor as fundamental for understanding traction in solid mechanics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Traction Vector
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
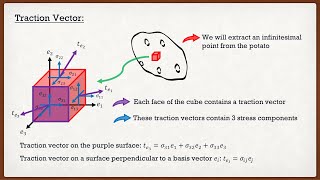
We had found the formula for traction at point x on an arbitrary plane with normal n (shown in Figure 1).
Detailed Explanation
In this chunk, we introduce the concept of the traction vector, which quantifies the force per unit area acting on a specific plane at a given point. The traction vector is determined based on the point in question, x, and the orientation of the normal vector, n, of the plane being considered.
Examples & Analogies
Imagine holding a piece of paper taut with one hand while pressing down on it with the other. The pressure you apply creates a traction vector on the surface of the paper, reflecting the force you exert relative to the area of contact.
Independence of Traction from Plane Selection
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But physically, this tn, the traction on the plane with normal n, has to be the same irrespective of what three planes were used to find out this traction.
Detailed Explanation
This chunk explains that the traction calculated for a given point on a specific plane does not depend on how we calculate it—that is, it remains constant regardless of the three planes chosen for the calculation. This property assures consistency in results.
Examples & Analogies
Consider a balloon. No matter which three directions you push from (top, side, bottom), you will still notice the tension in the material of the balloon remains the same. This illustrates the principle of independence related to the traction vector calculation.
Conclusion on Traction Vector
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus, the formula for tn is independent of what three planes are used.
Detailed Explanation
In summary, the traction vector derived from this concept indicates that the force experienced at point x remains consistent, ensuring that it does not vary due to the choice of planes. This independence is significant for further deriving relationships in mechanics, particularly regarding stress tensors.
Examples & Analogies
Think of a car experiencing the same acceleration regardless of the road’s incline. No matter how you approach measuring the force acting on it, the fundamental mechanics dictate it will remain constant, similar to how traction behaves in mechanics.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Traction Vector: Describes forces on surfaces, invariant to plane selection.
-
Stress Tensor: Represents internal force distribution in materials as a matrix.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When analyzing a bridge, the traction vector helps engineers understand where forces may concentrate.
-
In an experiment, applying different loads to a beam allows observation of how the stress tensor predicts deformation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Forces acting, the traction's the way, shows the direction of stress every day.
📖 Fascinating Stories
-
Imagine a group of students pushing on a large door from different angles. Each push represents a traction vector; together they determine how the door moves.
🧠 Other Memory Gems
-
Use 'T.I.P' to remember Traction Independence on Planes when you're calculating forces.
🎯 Super Acronyms
For the stress tensor, use 'STEM' meaning Stress Tensor Equally Multiplies forces to remember its importance.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Stress Tensor
Definition:
A mathematical representation of the internal distribution of forces within a material, encapsulated in a matrix format.
-
Term: Normal Vector
Definition:
A vector that is perpendicular to a given surface at a point.
-
Term: Tensor Product
Definition:
A mathematical operation that produces a matrix from two vectors, representing the stress tensor.