Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Loading Types
Unlock Audio Lesson
Today, we're going to talk about the different types of loading you might encounter when analyzing beams. Can someone tell me what they think a concentrated load might mean?
Isn’t that where a load is applied at a specific point on the beam?
Exactly! A concentrated load is applied at a single point. Now, can anyone give me an example of this type of load?
Like a weight sitting on a shelf?
Yes, that's a perfect example! Now there’s also distributed loads, which can be uniformly distributed or vary. Can anyone explain these types?
A uniformly distributed load spreads the load evenly across the beam, right?
Exactly! While a linearly varying distributed load changes intensity along the beam. Remember, think of UDL as even spread, and LVDU like a ramp. Let's move on to how supports interact with these loads.
Support Types
Unlock Audio Lesson
Moving on to supports, who can tell me what a roller support does?
It allows vertical movement but not horizontal, right?
Correct! Roller supports can provide vertical reactions but not resist horizontal forces. What about hinge supports?
They allow both vertical and horizontal reactions?
That's spot on! And finally, what is unique about fixed supports?
They provide vertical and horizontal reactions plus a bending moment?
Exactly! These reactions are crucial in determining the stability of a structure. Now, let’s tie this into the types of beams.
Beam Types
Unlock Audio Lesson
There are various types of beams in engineering. Can anyone identify a statically determinate beam?
A simply supported beam?
Yes! What about statically indeterminate beams?
A continuous beam! It has more supports than necessary?
Very good! Understanding these definitions will aid you later. Remember, simply supported beams are the most straightforward, while continuous beams offer more stability but are more complex to analyze.
Beam Reactions
Unlock Audio Lesson
Now let's get into beam reactions. Why do we need to calculate these?
To understand how the beam holds up the loads applied to it?
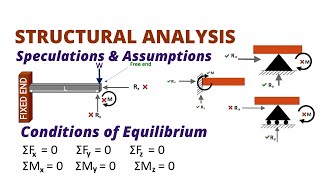
Absolutely! By using the free body diagram and the three equations of equilibrium—ΣF_x = 0, ΣF_y = 0, ΣM = 0—we can find these reactions. Can anyone summarize what those equations signify?
They ensure all horizontal and vertical forces and moments balance out?
Perfectly summarized! This balance is crucial for safe and effective structural design.
Sign Convention
Unlock Audio Lesson
Finally, let’s wrap up with the sign convention we're adopting. Can someone describe the positive directions for our forces?
The positive x-direction is to the right, and the positive y-direction is upward?
Exactly! And what about the positive moment?
Counter-clockwise, right?
Correct! Understanding this convention helps in maintaining clarity when we conduct our calculations. Let’s ensure these concepts are solid before we tackle examples.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the types of loads that can be applied to beams, categorize support types, and identify the various beam types. Importantly, we also analyze how reactions are developed in beams due to these loads, reinforced by sign conventions.
Detailed
Beam Analysis
This chapter delves into the fundamental aspects of beam analysis, which is crucial in the field of civil engineering and structural design. It begins with an overview of the loading on beams, distinguishing between concentrated and distributed loads, including Uniformly Distributed Load (UDL) and Linearly Varying Distributed Load (LVDU). This foundational understanding is essential as the loading directly influences how beams respond to structural loads.
Next, the section categorizes support types—roller, hinge, and fixed supports—that determine how loads are transferred to other structural members such as columns. Each type of support plays a critical role in ensuring stability and integrity in structures.
The analysis continues into different beam types, breaking down statically determinate and indeterminate beams alongside various configurations, like simply supported, continuous, cantilevers, and overhanging beams. Understanding these types allows engineers to select the appropriate beam for specific applications based on the load conditions and structure design requirements.
Additionally, the chapter emphasizes beam reactions, explaining how these reactions arise from applied loads and can be calculated using the three equations of equilibrium—crucial for designing and analyzing structures.
A sign convention is also introduced to maintain consistency in understanding the direction of forces and moments, providing clarity as students approach examples later in the section.
Finally, the section presents examples that illustrate beam behavior under various loads, creating a bridge between theoretical knowledge and practical application, underscoring the importance of internal forces, such as shear and bending moments, that are developed within beams.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Loading on Beams
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
2.1 Loading on Beams:
The loading on beam can be categorized to (Figure 2-1):
- Concentrated Load
- Concentrated Force
- Concentrated Moment
- Distributed Load
- Uniformly Distributed Load (UDL)
- Linearly Varying Distributed Load (LVDU)
Figure 2-1: Loading types on beams
Detailed Explanation
In beam analysis, the loads that act upon beams are crucial for understanding how they will perform structurally. There are mainly two types of loads: concentrated loads and distributed loads.
- Concentrated Load: This type of load is applied at a single point on the beam. It can be further broken down into:
- Concentrated Force: A force exerted at a specific point.
- Concentrated Moment: A moment or torque applied at a specific point, causing rotation about that point.
- Distributed Load: This load is spread over a length of the beam rather than acting at a single point. It can be categorized as:
- Uniformly Distributed Load (UDL): A load that is consistent across the beam length.
- Linearly Varying Distributed Load (LVDU): A load that changes linearly along the beam length, increasing or decreasing in intensity.
Examples & Analogies
Imagine holding a long, straight stick where one person applies a weight, like a backpack, at one specific point (this represents a concentrated load). Now, think about laying a blanket on the stick where various items are placed on it evenly (this represents a uniformly distributed load). This helps visualize how different loads affect the stick (or beam) differently.
Support Types
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
2.3 Support Types:
Supports on beams transfer the loads to the following structural member (usually a column).
Three major types (Figure 2-2):
- Roller: Vertical reaction only
- Hinge: Vertical and horizontal reaction
- Fixed: Vertical and horizontal reaction + a bending moment
Figure 2-2: Beam reaction types
Detailed Explanation
Supports are critical because they determine how the loads from the beam transfer to the structure. There are three major types of supports:
- Roller Support: This allows vertical movement but not horizontal movement. This means the roller can slide up and down, creating only a vertical reaction to the loads applied.
- Hinge Support: This allows both vertical and horizontal movement. It provides a more complex reaction than the roller support, being able to resist vertical forces as well as horizontal forces.
- Fixed Support: This type does not allow any movement at the ends of the beam, providing vertical and horizontal reactions as well as resisting bending moments, making it the most rigid type of support.
Examples & Analogies
Think of a seesaw (beam). If one end is propped up by a rock (roller), it can move up and down. If it’s held by a person (hinge), they can push it sideways too. And if it’s cemented to the ground (fixed), it can’t be moved at all! Each support type gives different stability and movements to the seesaw (the beam).
Beam Types
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
2.4 Beam Types:
Beams can be divided into (Figure 2-4):
- Statically determinate beams:
- Statically indeterminate beams:
- Simply supported beams
- Continuous beam
- One-sided over-hanging beam
- End-supported cantilever
- Two-sided over-hanging beam
- Fixed at both ends
- Cantilever beam
Figure 2-4: Beam types
Detailed Explanation
Beams can be classified based on how they are supported and the forces they experience:
- Statically Determinate Beams: These beams can be analyzed using only the equations of equilibrium, meaning all reactions at the supports can be determined directly from the applied loads.
- Statically Indeterminate Beams: These beams have more unknown support reactions than equations of equilibrium available, requiring additional analysis methods (like compatibility conditions) to solve.
Categories of Beams:
- Simply Supported Beams: Supported at both ends, free to rotate.
- Continuous Beams: Extend over more than two supports.
- Overhanging Beams: Project beyond their support on one or both ends.
- Cantilever Beams: Fixed at one end and free at the other, crucial in many structural scenarios.
Examples & Analogies
Consider a diving board (cantilever beam) at one end of a swimming pool, where the other end is firmly fixed. If you walk on it (interpreting loads), it bends downwards. A bridge (continuous beam) that spans the river over multiple columns can handle many cars (loads) while remaining stable. Both examples help illustrate the varying types of beams employed based on load and support situations.
Beam Reactions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
2.5 Beam Reactions:
- Reactions on beams are developed due to the applications of the various loads on the beam.
- The reactions can be calculated (determinate beams only) by applying the three equations of equilibrium after drawing the free body diagram of the beam.
- The three equations of equilibrium are:
A3F_x = 0
A3F_y = 0
A3M = 0
Figure 2-5: Beam reaction types
Detailed Explanation
When loads are applied to a beam, reactions occur at the supports which must be calculated to ensure structural integrity. The reactions can only be calculated directly for statically determinate beams using the three fundamental equations of equilibrium:
1. Sum of Horizontal Forces (∑F_x = 0): The total horizontal forces must balance, ensuring no lateral movement.
2. Sum of Vertical Forces (∑F_y = 0): The total vertical forces must also balance to prevent vertical movement.
3. Sum of Moments (∑M = 0): The moments about any point must balance to ensure there’s no rotation.
These conditions must all be satisfied for an equilibrium state.
Examples & Analogies
Think about balancing a seesaw at the playground. If one kid is heavier (applying more load), the other side (the support) needs to adjust to keep it level. Similarly, in engineering, we must ensure that forces and moments on the beam balance out so that the structure remains stable, just like how you’d operate a seesaw.
Sign Convention
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
2.6 Sign Convention:
The positive sign convention used throughout the course is summarized in Figure 2-6. The positive x-direction is taken to the right, the positive y-direction is taken upward, and the positive moment is taken in the counter-clockwise direction.
Detailed Explanation
In engineering, establishing a clear sign convention is essential for consistently analyzing forces and moments. The conventions used in beam analysis specify the following:
- Positive x-direction: Forces moving to the right are considered positive.
- Positive y-direction: Forces moving upwards are considered positive.
- Positive Moment: A rotation that occurs counter-clockwise is considered positive.
These conventions help ensure that everyone working on the project interprets forces and moments in the same way, which is crucial for collaboration and correctness.
Examples & Analogies
Think of how we read maps – north is always up. Similarly, in engineering analysis, certain predefined rules (sign conventions) tell us how to interpret forces. If everyone has the same understanding, then projects – like building bridges or skyscrapers – will proceed without confusion, much like teams navigating together using the same map.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Concentrated Load: A load that is applied at a specific point on a beam.
-
Distributed Load: A load spread over a length of a beam rather than being concentrated at one point.
-
Support Types: The methods through which beams are held, affecting stability and load distribution.
-
Beam Types: Classifications based on how the beams are supported and their ability to carry loads.
-
Reactions: Forces that occur in response to loads applied on beams, crucial for equilibrium.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A concentrated load may occur when a weight is placed at the center of a simply supported beam.
-
A uniformly distributed load can be seen in structures like bridges where the weight is evenly spread across the surface.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a concentrated load's tight embrace, one weight sits in just one place.
📖 Fascinating Stories
-
Imagine a strong beam being challenged by both heavy weights and gentle pushes. Each load applies pressure, while the supports hold firm, ensuring balance through teamwork.
🧠 Other Memory Gems
-
Remember 'CRF': Concentrated, Roller, Fixed supports for an easy recall of beam supports.
🎯 Super Acronyms
Think 'STAB' for Beam Types
- Statically determinate
- Statically indeterminate
- Additional types.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Concentrated Load
Definition:
A load applied at a single point on a beam.
-
Term: Distributed Load
Definition:
A load applied over a length of the beam instead of a single point.
-
Term: Uniformly Distributed Load (UDL)
Definition:
A type of distributed load where loads are applied evenly across the beam.
-
Term: Linearly Varying Distributed Load (LVDU)
Definition:
A distributed load that varies linearly along the length of the beam.
-
Term: Support Types
Definition:
Various methods in which a beam is supported, affecting how loads are transferred.
-
Term: Fixed Support
Definition:
A support that can resist vertical and horizontal forces as well as moments.
-
Term: Equilibrium
Definition:
A state where the sum of all forces and moments acting on the beam is zero.