Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Procedure for Analysis
Unlock Audio Lesson
Welcome, class! Today we will learn about the procedure for analyzing internal forces in beams. Can anyone tell me why we need to determine these forces?
We need to ensure the structural integrity of beams.
Exactly! Let’s start with the first step: computing support reactions. Remember the acronym SEEP: Support, External forces, Equilibrium, and Portion selection. Can anyone recall what we do in this step?
We apply equilibrium equations to find the support reactions on the beam, right?
Right! Now, in cantilever beams, we might skip this by analyzing the free portion instead. That’s a little trick to remember! Moving on, what’s the next step?
Cut the beam at the desired location.
Exactly! By passing a section where we want to analyze forces, we simplify the next calculations. Let’s look at how we select which beam portion to analyze next.
We look for the portion with fewer external forces.
Correct! This keeps our calculations simpler. Remember, simpler is better!
To summarize, first compute support reactions, cut the beam, and choose the portion. We'll cover the next steps next class.
Calculating Forces: Axial, Shear, and Bending Moment
Unlock Audio Lesson
Today we’ll discuss calculating the internal forces starting with axial force. Who can explain how we can do that?
We sum the external loads in the direction of the beam's axis.
Yes! The axial force is simply the sum of these forces. Let's remember 'ASAP' – 'Axial Sum Action'. Now, how about shear?
We add the components of forces perpendicular to the axis.
Exactly! We compute shear forces by summing perpendicular components. To summarize: Axial = Sum of parallel forces, Shear = Sum of perpendicular forces. Now, who would like to tackle bending moments?
That’s about taking moments around the section we cut, right?
Correct! Moments are calculated by summing the moments of external forces around that section. Make sure to grasp this as it’s essential for the next topic: verification.
How do we verify our calculations?
Good question! We can check our results using the other beam portion. If they're identical, our work is solid. Remember the formulae involved and stay engaged!
Using the Procedure: Practical Applications
Unlock Audio Lesson
Now that we understand the theory, let’s apply this to real-world examples. Who would like to present their analysis of a beam?
I have a beam with a concentrated load. I found the support reactions first.
Great job! What did you find next?
I cut the beam at the load location to analyze axial force.
Did you find the shear force next?
Yes! I calculated the shear by summing the forces perpendicular to the axis.
Excellent! It's key to keep the order right: Axial, then Shear, then Bending Moment. Anyone else wants to share their process?
I used another example with a distributed load, and it was tricky!
Distributed loads can be complicated. Always look at applying the same steps systematically. Revisit each step and verify your work afterwards.
For homework, I want each of you to analyze a beam with a different load type and bring your steps to the next class.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section provides a step-by-step procedure for determining support reactions and analyzing internal forces at specified points on a beam. Key steps include computing support reactions, determining axial forces, shear forces, and bending moments, with an emphasis on verifying results for accuracy.
Detailed
Theory of Structures
This section describes the methodical approach to analyzing internal forces within beams, a critical aspect of structural engineering. The procedure consists of several methodical steps:
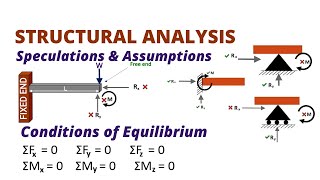
- Compute Support Reactions: Begin by applying equilibrium equations to find the support reactions. For cantilever beams, you may ignore this step by analyzing the free portion.
- Cutting the Beam: Introduce a section perpendicular to the centroidal axis at the desired point of analysis, thus dividing the beam into two sections.
- Selecting Beam Portion: Choose the beam portion with fewer external loads or no reactions for simplicity in calculations.
- Determine Axial Force: Sum the forces parallel to the beam axis to find the axial force.
- Determine Shear Force: Calculate the shear force by summing the perpendicular components of external forces.
- Determine Bending Moment: Find the bending moment by evaluating moments around the section due to external forces and couples.
- Verification: Optionally repeat calculations using the unutilized portion of the beam to verify accuracy.
The section concludes with exercises urging students to apply these principles to specific examples.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Procedure for Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The procedure for determining internal forces at a specified location on a beam can be summarized as follows:
Detailed Explanation
This introduction sets the stage for understanding how to analyze beams in structural engineering. It suggests that there is a systematic approach to determining internal forces, which is essential for ensuring structures are stable and safe.
Examples & Analogies
Think of analyzing a beam like checking the stability of a bridge. Just as engineers need to consider various forces acting on the bridge, we must analyze internal forces within the beams that hold it up.
Step 1: Compute the Support Reactions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
1- Compute the support reactions by applying the equations of equilibrium and condition (if any) to the free body of the entire beam. In cantilever beams, this step can be avoided by selecting the free, or externally unsupported, portion of the beam for analysis.
Detailed Explanation
In this step, we calculate the reactions at the supports of the beam. These reactions are the forces exerted by the supports to keep the beam in equilibrium. If we are analyzing a cantilever beam (which is supported at only one end), we can simplify things by focusing on the unsupported portion.
Examples & Analogies
Imagine a seesaw. The point where it rests (the support) reacts to all the weight on either side. If one side is unsupported, a lot of the analysis can focus on just that side, making calculations easier.
Step 2: Pass a Section Perpendicular to the Beam
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
2- Pass a section perpendicular to the centroidal axis of the beam at the point where the internal forces are desired, thereby cutting the beam into two portions.
Detailed Explanation
Here, we are instructed to make an imaginary cut in the beam where we want to analyze internal forces. This cut divides the beam into two parts, enabling us to examine the forces and moments acting on either side of the cut.
Examples & Analogies
Think of slicing a cake. If you want to check how much icing is on a specific piece, you cut a slice and look at the frosting on that piece rather than the whole cake.
Step 3: Select the Portion with Less Computational Effort
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
3- Although either of the two portions of the beam can be used for computing internal forces, we should select the portion that will require the least amount of computational effort, such as the portion that does not have any reactions acting on it or that has the least number of external loads and reactions applied to it.
Detailed Explanation
Choosing which side of the beam to analyze is critical. Selecting the portion that simplifies calculations reduces potential errors and saves time. This is particularly important when the chosen side has no reactions or fewer loads.
Examples & Analogies
Imagine you have a heavy backpack. It's easier to analyze and see if you can lift it if you only examine one side instead of trying to assess both sides at once.
Step 4: Determine the Axial Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
4- Determine the axial force at the section by algebraically summing the components in the direction parallel to the axis of the beam of all the external loads and support reactions acting on the selected portion.
Detailed Explanation
This step involves calculating the axial forces that act along the length of the beam. We do this by adding up all the loads and reactions acting parallel to the beam's axis to determine the resultant axial force at the cut section.
Examples & Analogies
Think of a tug-of-war game. The total force exerted by both teams pulls in different directions. When assessing the strength of the rope, we need to sum how strongly each team is pulling.
Step 5: Determine the Shear Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
5- Determine the shear at the section by algebraically summing the components in the direction perpendicular to the axis of the beam of all the external loads and reactions acting on the selected portion.
Detailed Explanation
In this step, we focus on calculating the shear forces, which act perpendicular to the beam's length. Just like axial forces, we sum all the forces acting in the vertical direction at the section to find the total shear force.
Examples & Analogies
Imagine a stack of books on a table. If someone pushes the top book to one side, the pushing force represents shear. We calculate this force to understand how much resistance the stack can handle.
Step 6: Determine the Bending Moment
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
6- Determine the bending moment at the section by algebraically summing the moments about the section of all the external forces plus the moments of any external couples acting on the selected portion.
Detailed Explanation
The bending moment indicates how much a beam bends under load. We calculate it by summing the moments, produced by external forces and couples, about the cut section. Moments are calculated as the force multiplied by the distance from the point of interest.
Examples & Analogies
Picture a seesaw again. If one side is pushed down, the moment around the pivot changes. Understanding how these moments work helps us ensure that the seesaw remains balanced.
Step 7: Verify the Calculations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
7- To check the calculations, values of some or all of the internal forces may be computed by using the portion of the beam not utilized in steps 4 through 6. If the analysis has been performed correctly, then the results based on both left and right portions must be identical.
Detailed Explanation
Verification is a crucial step in the analysis. By calculating the internal forces on the other side of the cut section, we ensure consistency in our results. If both calculations yield the same results, our analysis is likely correct.
Examples & Analogies
Think of double-checking your homework answers. If the same question yields the same answer regardless of which route you take to get there, you can be more confident in your solution.
Conclusion & Examples
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For the following examples, determine the axial forces, shears, and bending moments at points A and B of the structure shown.
Detailed Explanation
After discussing the procedure for analyzing internal forces in beams, the text provides examples to apply this knowledge. Working through examples reinforces the learned concepts and demonstrates their practical application.
Examples & Analogies
Consider learning to ride a bicycle. Initially, you learn the theory of pedaling, balancing, and steering. By practicing on a real bike, you can apply what you've learned – this transition from theory to practice is similar to what happens when students work with examples.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Axial Force: The internal force acting along the beam's length.
-
Shear Force: The internal force acting perpendicular to the beam's length.
-
Bending Moment: The moment that results in the bending of the beam due to external loads.
-
Equilibrium: Conditions under which a beam remains stationary and balanced under external loads.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Calculation of axial forces in a statically determinate beam with a concentrated load.
-
Example 2: Determination of shear forces in a simply supported beam under uniform load.
-
Example 3: Bending moment calculation at a point on a cantilever beam with point loading.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Axial, Shear, then Moment come dear, keep them in mind when analyzing here!
📖 Fascinating Stories
-
Imagine a beam named Benny. Benny gets loads from the left and right. He feels pressure (shear) but keeps his balance (moment) at the center. Always check Benny before he bends!
🧠 Other Memory Gems
-
Remember: A - Analyze support reactions, C - Cut sections, S - Select portions, U - Ultimate forces.
🎯 Super Acronyms
Remember 'ASAP' for Axial, Shear, and Moment calculations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Support Reactions
Definition:
Forces developed at the supports of a beam to maintain equilibrium.
-
Term: Axial Force
Definition:
A force that acts along the length of the beam.
-
Term: Shear Force
Definition:
A force acting perpendicular to the length of the beam.
-
Term: Bending Moment
Definition:
A measure of the internal moment that induces bending in a beam.
-
Term: Equilibrium
Definition:
A state where all forces and moments are balanced.
-
Term: Centroidal Axis
Definition:
An imaginary line that passes through the centroid of a beam's cross-section.