Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Structural Geometry
Unlock Audio Lesson
Today we're discussing the Magazini Generali and its remarkable geometry. Why do you think the shape of a structure is important?
I think it might affect how strong the building is?
Yeah, the shape could also influence how it looks!
Exactly! The internal supporting frames' shape is critical for both stability and aesthetic appeal. We can summarize this using the acronym SAFE: Structure, Aesthetics, Functionality, and Efficiency.
What does each part of SAFE stand for again?
Sure! SAFE stands for Structure for stability, Aesthetics for beauty, Functionality for use, and Efficiency for performance. This concept is fundamental in architecture.
Calculating Loads
Unlock Audio Lesson
Next, let's move on to how we calculate the loads acting on the Magazini Generali. What load factors do we need to consider?
The weight of the roof and the frame itself, right?
And we need to know how to combine them!
Correct! The total uniform load can be found by adding the roof load and the frame weight. If we use examples like 98 psf for the roof load and 13.6 kips for the frame, what would our total load be?
I think it's 1.6 k/ft by adding them together.
Exactly! Being comfortable with these calculations is crucial for understanding structural design.
Reactions and Internal Forces
Unlock Audio Lesson
Now, let's connect our understanding to the reactions in the beam. How do we calculate the reaction forces?
We can use the total weight and divide it since the beam is symmetrical?
That gives us each reaction force at 51 k!
Exactly right! These reactions are supported by internal shear forces. Let's also review how we determine the shear and moment diagrams in this context.
Understanding Shear and Moments
Unlock Audio Lesson
Finally, we need to discuss the nature of shear and moment forces within the beam. What happens to the shear across the length of the beam?
It changes from positive to negative?
And there's a maximum moment at the center, right?
Correct! The moment is maximum at midspan, which we can calculate using the formula M = qL²/8. Understanding these concepts helps us design safe and functional structures.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
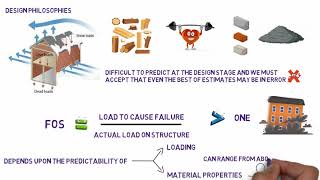
In this section, we explore the geometrical aspects of the Magazini Generali storage house, highlighting how Maillart's design integrates aesthetic appeal with engineering efficiency. Key concepts include the shape of internal supporting frames, load calculations, and the internal forces acting within the structure.
Detailed
Geometry
This section analyzes the geometrical features of the Magazini Generali, a storage house designed by Maillart in 1924. It showcases a remarkable blend of aesthetics and engineering, particularly evident in the shape of its internal supporting frames, which influence both structural integrity and visual appeal. The design includes idealized beams supported by cantilever columns, crafted to minimize moment transmission to the foundations. Furthermore, the section includes calculations of loads from roof slabs and frames, revealing how these contribute to the total structural load. We also discuss reaction forces, shear forces, and moments, emphasizing their critical role in maintaining equilibrium within a uniformly loaded beam system.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Magazini Generali
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This storage house, built by Maillart in Chiasso in 1924, provides a good example of the marriage between aesthetic and engineering.
Detailed Explanation
The Magazini Generali building exemplifies how architecture can blend beauty with structural engineering. Designed by Maillart in 1924, it highlights how the visual appeal of a structure can be integrated with the principles of engineering. The concept discussed here emphasizes that effective architectural design does not sacrifice functionality for aesthetics but rather brings them together seamlessly.
Examples & Analogies
Think of a well-designed smartphone that is not only visually striking but also highly functional. Just like the phone combines attractive design with useful features, the Magazini Generali building combines beauty with the engineering challenges of supporting the structure.
Supporting Frames
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The most striking feature of the Magazini Generali is not the structure itself, but rather the shape of its internal supporting frames, Fig. 32.1.
Detailed Explanation
The internal supporting frames of the Magazini Generali are noteworthy as they play a crucial role in sustaining the building. These frames are designed to handle the structural loads while also providing an interesting visual outline. The shape and configuration of these frames are essential not just for stability, but they also contribute to the overall aesthetic appeal of the building.
Examples & Analogies
Consider a suspension bridge, where the cables and towers create an iconic silhouette against the skyline. Just like those cables must be structurally sound while creating an attractive shape, the supporting frames in Magazini Generali must also ensure stability while being visually appealing.
Beam and Column Support Structure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The frame can be idealized as a simply supported beam hung from two cantilever column supports. Whereas the beam itself is a simple structural idealization, the overhang is designed in such a way as to minimize the net moment to be transmitted to the supports (foundations), Fig. 32.2.
Detailed Explanation
The building's frame can be visualized as a beam that is supported at its ends by columns that extend outward (cantilevered). This design helps to reduce the forces, or moments, that are transmitted to the foundation, ensuring that the structure remains stable and secure. The idealization simplifies our understanding of the complex forces at work within the building's design.
Examples & Analogies
Imagine a diving board that is anchored at one end while extending out over the pool. The way the board extends out minimizes the stress on the anchor point. Similarly, the overhang in the Magazini Generali reduces the amount of weight and force that the supports have to bear, making the entire structure more efficient.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Structural Integrity: The ability of a structure to withstand its intended load without failure.
-
Aesthetic Design: The visual aspects that contribute to the overall attractiveness and harmony of a structure.
-
Load Calculation: The process of determining the weights and forces acting on a structure.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In Magazini Generali, the design incorporates a cantilever structure, allowing for extended overhangs that enhance both aesthetics and stability.
-
The calculation of loads shows how the roof weight of 98 psf contributes to a uniform total load, important for determining support requirements.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Beams above, strong and bright, hold the roofs, day and night.
📖 Fascinating Stories
-
Imagine a cantilever beam hanging over a pool, strong enough to hold the weight and look fabulous while doing it!
🧠 Other Memory Gems
-
For LOAD: L for Lump, O for Overhead, A for All, D for Distributed. This helps remember what types of loads to consider.
🎯 Super Acronyms
SHAPE = Stability, Harmony, Aesthetic, Performance, Efficiency.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Beam
Definition:
A long, horizontal structural element supported at its ends.
-
Term: Cantilever Column
Definition:
A column that is fixed at one end and free at the other.
-
Term: Uniform Load
Definition:
A load that is evenly distributed over a structural element.
-
Term: Shear Force
Definition:
The internal force that acts along the length of a beam, resulting from external loads.
-
Term: Moment
Definition:
The measure of the rotational effect of a force about a point.