Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Rigid Bar and Spring System
Unlock Audio Lesson
Today, we'll learn about the analogy between a rigid bar stability and the dynamics of a mass-spring system. Can anyone describe what a rigid bar connected by springs might look like?
It’s like a bar held at one end with springs allowing it to sway.
Exactly! And when we think of a two-degree-of-freedom mass-spring system, we can visualize two masses acting like that bar. What forces do you think affect these masses?
The spring force and the inertial force from the acceleration.
Right! The inertial force is calculated as mass times acceleration. Let's remember it with the acronym ‘F=ma’. How does it apply here?
It means the more mass we have, the greater the force when accelerating.
Perfect! So, the rigid bar and mass-spring system share the behavior of responding to applied forces similarly.
To summarize, both systems showcase how forces interact to maintain stability.
Equations of Motion
Unlock Audio Lesson
Let’s explore the equations of motion for each mass. The motion is described through second-order differential equations. Who can summarize this?
Each mass has its motion tied to the spring forces and it creates a differential equation.
Correct! Specifically, for mass `m1`, the equation is `m1 * u1'' + k1 * (u1 - u2) = 0`. What about for mass `m2`?
`m2 * u2'' + k2 * (u2 - u1) = 0`!
Well done! Remember, the motion of these masses interacts and affects each other.
To summarize, the interaction between masses indicates how systems can be interconnected dynamically.
Matrix Representation
Unlock Audio Lesson
Next, let's talk about representing the equations of motion in matrix form. Why do you think we might do this?
It simplifies the calculations and makes it easier to deal with multiple equations.
Exactly! In matrix form, we construct a system using mass and stiffness matrices. Can someone give me an example of how it looks?
It looks like `M U' + K U = 0` where `U` represents the displacement vector.
Right! This representation is critical in analyzing systems thoroughly. Always keep in mind the relationships between components.
In conclusion, matrix representation provides an efficient means for handling complex problems.
Characteristic Equation and Natural Frequency
Unlock Audio Lesson
Finally, let's discuss the characteristic equation, `K(λ) = M`, relating stiffness and mass. Who can explain what this represents?
It helps us find the natural frequencies of the system!
That's right! The natural frequency gives us insights into how the system will react to disturbances.
So higher stiffness means higher frequency?
Correct! To summarize, understanding natural frequencies can help predict a system's response to loading.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section draws parallels between the equilibrium of a rigid bar under axial load and the dynamics of a two-degree-of-freedom mass-spring system, highlighting key principles of equilibrium, inertia, and forces at play.
Detailed
Analogy with Free Vibration
This section discusses the significant similarities between the stability of a rigid bar system and the vibration characteristics of a two-degree-of-freedom mass-spring system. When analyzing both systems, the forces acting on each mass in a dynamic system, as well as their inertial properties, can be represented via a mathematical model.
Key Points Covered:
- System Description: The mass-spring system consists of two masses,
m1andm2, connected by springsk1andk2. The dynamics of these masses can be described using Newton's laws, where each mass experiences inertial forces proportional to their acceleration. - Equations governing the motion are framed using Hooke's law.
- Equations of Motion: The motion of both masses is governed by second-order differential equations, which incorporate both spring forces and inertial forces:
- For mass
m1:m1 * u1'' + k1 * (u1 - u2) = 0 -
For mass
m2:m2 * u2'' + k2 * (u2 - u1) = 0 - Matrix Representation: The equations can be represented in matrix form for a clearer analysis involving matrix operations in eigenvalue problems. The interaction between the masses and springs showcases coupled motion.
-
Characteristic Equation: Understanding the characteristics of vibrations involves constructing a characteristic equation that links stiffness (
K) and mass (M) matrices.
Thus, this section serves to illustrate how insights from mechanical vibration topics can enhance understanding rigid bar stability concepts, emphasizing an integrated approach in structural engineering. Understanding vibrational principles equips engineers with skills to predict responses to loads, thereby fostering stability assessments in structural applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Analogous Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
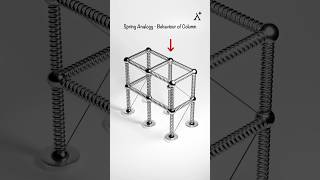
The problem just considered bears great resemblance with the vibration of a two degree of freedom mass spring system, Fig. 18.4.
Detailed Explanation
In this chunk, we highlight how the problem of stability that previously discussed is similar to a mass-spring system with two degrees of freedom. This implies that both systems behave in ways that can be described using similar physical laws despite their different contexts.
Examples & Analogies
You can think of this analogy like a seesaw. If one side is pushed down (like applying a load to our bar), the other side lifts up. If you let go, the seesaw will vibrate up and down until it settles in a stable position, similar to how our two-degree freedom system vibrates until it reaches a stable state.
Equations of Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Each mass is subjected to an inertial force equals to the mass times the acceleration, and the spring force: 2mü + ku + k(u2 - u1) = 0 (18.14-a)
m1ü1 + ku1 + k(u2 - u1) = 0 (18.14-b)
Detailed Explanation
This section provides the equations of motion for the two mass-spring system. The first equation shows that the sum of forces acting on each mass (inertia force and spring forces) equals zero, meaning the system is in equilibrium. These equations help us analyze how the system will behave over time.
Examples & Analogies
Imagine two people sitting on a connected trampoline. If one jumps, it affects how the other person moves up and down. The equations illustrate that each person's movement is interconnected, just like the two masses in our spring system.
Matrix Formulation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
or in matrix form: M Ü + K U = 0, where M is the mass matrix and K is the stiffness matrix.
Detailed Explanation
This chunk states that when we arrange the equations of motion in matrix form, we simplify the process of solving for system behaviors. M represents how the mass is distributed in the system, while K represents how the system resists deformation (its stiffness). By using matrices, we can handle complex systems more easily.
Examples & Analogies
Think of a matrix like a recipe that mixes different ingredients (masses and springs) to create a dish (the system’s movement). Rather than dealing with each ingredient separately, the recipe provides a structured way to combine and analyze them all at once.
Characteristic Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The characteristic equation is K(λ) - M = 0 where λ = ω², and ω is the natural frequency.
Detailed Explanation
The characteristic equation is crucial because it helps us determine the natural frequencies of the system, which are the frequencies at which the system tends to vibrate when not subjected to external forces. Finding these frequencies is key to understanding the behavior of any dynamic system.
Examples & Analogies
Consider a swing. It has a natural frequency determined by its length and the force of gravity. When you push the swing at exactly the right moments (its natural frequency), it goes higher and higher. Our characteristic equation tells us how to find those moments for our mass-spring system.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Rigid Bar Stability: The balance of forces acting on a rigid bar supported by springs.
-
Mass-Spring System: A system that behaves dynamically when masses and springs are interconnected.
-
Equations of Motion: Mathematical formulations that describe the dynamics of a system.
-
Characteristic Equation: An essential equation used in systems analysis to find frequencies.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Consider a mass-spring system with two masses, each affected by the spring forces and the acceleration due to gravity. This showcases how mass distribution affects dynamic behavior.
-
An engineer may analyze a building's swaying during an earthquake, likening it to a two-degree-of-freedom dynamic system to assess stability.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a springy state, with mass and weight, vibrations sound like a melody straight.
📖 Fascinating Stories
-
Imagine a dancer on springs; when she jumps (force), she sways side to side—this is like our mass-spring system.
🧠 Other Memory Gems
-
To remember the steps: M for mass, K for spring—together, they sing in vibrational swing!
🎯 Super Acronyms
FMS for Free Mass Spring
- Forces
- Modes
- Stability.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Inertial Force
Definition:
The force acting on a mass proportional to its acceleration, calculated as mass times acceleration.
-
Term: Equilibrium
Definition:
A state in which the sum of forces and moments acting on an object is zero.
-
Term: Characteristic Equation
Definition:
An equation that relates the stiffness and mass matrices to determine natural frequencies.
-
Term: Natural Frequency
Definition:
The frequency at which a system tends to oscillate in the absence of any driving force.