Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Types of Connections
Unlock Audio Lesson
Today we are discussing the different types of beam-column connections we can have in structural frames. Can anyone tell me the three main types?
I think they're flexible, rigid, and semi-rigid.
Exactly! Let's dive into flexible connections first. Flexible connections act like hinges. What do you think that implies about their ability to resist moments?
They won’t resist moments at all, right? Both ends of the connection would have zero moments.
Correct! Remember, in a flexible connection, both end moments are zero. Now, how about rigid connections?
Rigid connections can transmit moments, so they would have non-zero end moments.
Exactly! Which leads to equal rotations at the ends. So if the beam is in a rigid connection with the column, both ends will rotate uniformly under load. Let's summarize this key point: For rigid connections, M = 0 and θ_C = θ_B.
Behavior of Simple Frames
Unlock Audio Lesson
Now let's consider how these connections influence the behavior of frames under vertical loads. When loads act on a frame, what do you think happens to the moments in rigid connections?
I guess the maximum moment in the beam would be reduced because the rigid connection shares the load.
Right! A rigid connection effectively distributes the load, which helps reduce undue stress. Can anyone explain what happens at the ends of the beam in this case?
There would be negative moments at the ends, but those would transfer to the columns, right?
Spot on! This interaction is vital for ensuring structural integrity. Remember, the interplay of moments helps maintain stability in frames, and that's why we need to understand these concepts.
Semi-Rigid Connections
Unlock Audio Lesson
Let’s shift to semi-rigid connections. How do they differ from flexible and rigid connections?
I think they can have non-zero moments just like the rigid ones, but the rotations don’t have to be equal.
Exactly! In semi-rigid connections, we have equal end moments, but the rotations differ. This behavior is accommodated by a spring mechanism. What does this say about the flexibility in design?
It means we can design for a balance between rigidity and flexibility depending on the loads!
Great insight! Balancing these characteristics is ultimately crucial for effective structural design.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explores beam-column connections, detailing their characteristics and effects on frame structure behavior. It differentiates between flexible, rigid, and semi-rigid connections and their influence on load distribution and deformation.
Detailed
Detailed Summary
This section provides an in-depth look at the concept of frames in structural engineering. Key relationships between beams and columns are analyzed, focusing on the three types of connections: flexible, rigid, and semi-rigid.
Connection Types
- Flexible Connections:
- Function as hinges that can only transfer forces, leading to cantilever action.
- Results in both end moments being equal to zero (M = 0).
- Rotations at the connected members are not equal.
- Rigid Connections:
- Allow moment transfer between sections, leading to equal end moments and rotations (M = 0, θ_C = θ_B).
- Crucial in maintaining structural integrity under vertical loads.
- Semi-Rigid Connections:
- Exhibit characteristics of both flexible and rigid connections.
- Have equal end moments that are non-zero while rotations differ.
- Resistance to rotation differences is provided through a spring mechanism.
Behavior of Simple Frames
The section illustrates how rigid connections mitigate the maximum moment in beams under loads, affecting the moment distribution throughout the frame. This sets the stage for understanding their behavior under various loading conditions and informs design considerations for structural engineers.
Overall, this section sets a foundational understanding of structural frame connections essential for further design and analysis discussions in structural engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Beam Column Connections
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
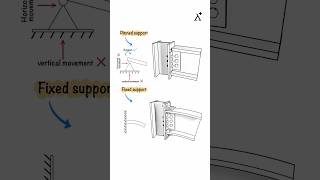
The connection between the beam and the column can be, Fig. 33.1:
1. Flexible
2. Rigid
3. Semi-Flexible
Flexible: that is a hinge which can transfer forces only. In this case we really have cantilever action only. In a flexible connection the column and beam end moments are both equal to zero, M = M = 0. The end rotation are not equal, \( \theta_{col} \neq \theta_{beam} \).
Rigid: The connection is such that \( \theta_{col} = \theta_{beam} \) and moment can be transmitted through the beam-column connection. In a rigid connection, the end moments and rotations are equal (unless there is an externally applied moment at the node), M = M = 0, \( \theta_{col} = \theta_{beam} \).
Semi-Rigid: The end moments are equal and not equal to zero, but the rotations are different. \( \theta_{col} \neq \theta_{beam} \), M = M = 0. Furthermore, the difference in rotation is resisted by the spring.
Detailed Explanation
The connections in a frame structure are crucial because they determine how beams and columns interact under loads.
- Flexible Connections: These do not resist moment. They act as hinges allowing rotation but cannot transfer bending forces. The moments at both ends of the beam are zero, indicating no bending occurs.
- Rigid Connections: These allow for the transfer of moments between the beam and the column. Both ends of the beam can resist bending and the rotation at both ends will be equal. This provides strength to the structure under loads.
- Semi-Rigid Connections: These are partially flexible and allow for some moment transfer but not completely. The moments may be the same at the ends but rotation will differ, creating a need for additional resistance in the form of springs.
Examples & Analogies
Consider a bicycle frame as an analogy. The joints where the handlebars connect to the frame can be thought of in similar terms. A flexible joint (like a hinge) would allow the handlebars to turn freely without much resistance, while a rigid joint would keep them firmly attached, allowing for no rotation but steady control. Semi-rigid would be like a joint that can bend a little but still allows some control.
Behavior of Simple Frames
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For vertical load across the beam, a rigid connection will reduce the maximum moment in the beam (at the expense of a negative moment at the ends which will in turn be transferred to the column).
Detailed Explanation
In frame structures when a vertical load is applied:
- Rigid connections have the significant benefit of reducing the maximum bending moment experienced in the middle of a beam. This is important because high bending moments can lead to failure. The trade-off is that negative moments occur at the ends of the beam due to the rigid connection's nature, which are transferred to the column supporting the beam. Thus, while the beam experiences a reduction in bending, it imparts some stress to the columns at the base.
Examples & Analogies
Imagine a tightly held flagpole in the wind. When the wind pushes against it (vertical load), the bottom of the pole (the columns) feels extra pressure even though the flag itself (the beam) isn't bending much. While the midsection remains sturdy, the anchoring at the base absorbs some of the pressure translated from the wind's force through the rigid connection keeping it upright.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Flexible Connections: Transfer forces with zero moments.
-
Rigid Connections: Allow moment transfer with equal rotations.
-
Semi-Rigid Connections: Equal non-zero moments with differing rotations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a flexible connection, such as in a cantilever beam setup, the beam's end moment is zero, allowing it only to experience axial and shear forces.
-
A rigid connection in a building frame not only allows for moment transfer to maintain structural integrity but also ensures that all connected sections respond uniformly to loads.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Flexible is free, with moments at zero, rigid stands strong, in a structural superhero.
📖 Fascinating Stories
-
In a grand old building, the rigid columns stood tall, sharing loads with grace, inspiring awe in all. The listeners learned how semi-rigid gave a flexible charm, as every connection held steady, safe from harm.
🧠 Other Memory Gems
-
Remember 'F R S' for Flexible, Rigid, and Semi-Rigid connections.
🎯 Super Acronyms
FRS
- 'Flexible
- Rigid
- Semi-Rigid' for memory aid.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Flexible Connection
Definition:
A joint that transfers forces only and has zero moments at the ends.
-
Term: Rigid Connection
Definition:
A joint that allows moment transfer, ensuring equal moments and rotations at the connected members.
-
Term: SemiRigid Connection
Definition:
A joint that has equal non-zero moments at the ends but differing rotations, with resistance provided by a spring.
-
Term: End Moments
Definition:
Moments acting at the ends of a structural member, crucial for load distribution.
-
Term: Cantilever Action
Definition:
The condition in a flexible connection where only the beam behaves as a cantilever due to zero moments.