Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Curves
Unlock Audio Lesson
Let's begin with the definition of curves. In road and railway design, curves help us connect two points that cannot be directly linked by straight lines due to natural terrain. Can anyone explain what types of curves we might find in this context?
Are horizontal and vertical curves the main types we study?
Exactly, Student_1! Horizontal curves change direction, while vertical curves change slope. Both are crucial for safe navigation. Why do you think it's important to design these curves carefully?
To ensure drivers have a smooth experience and to maintain safety on roads!
Yes! Let's remember that smooth transitions help maintain vehicle stability. Curves ensure we don't have abrupt direction changes that might lead to accidents.
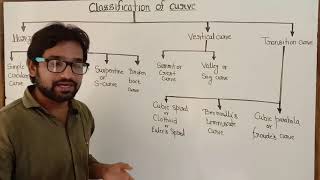
Types of Horizontal Curves
Unlock Audio Lesson
We have four main types of horizontal curves: simple, compound, reverse, and transition. Can anyone describe a simple curve for us?
A simple curve connects two straight sections with a single arc, right?
Precisely, well done! Now, what about a compound curve?
Is that when two arcs of different radii bend in the same direction?
Yes! Good job, Student_4! Compound curves help in locations where more gradual transitions are needed. Reverse curves, on the other hand, curve in opposite directions. Why might we want to avoid these on high-speed roads?
Because they could cause sudden jerks that might be dangerous at high speeds?
Very much so! Now, the transition curve is slightly different. Can someone explain its purpose?
It gradually introduces the centrifugal force to prevent sudden force on vehicles.
Excellent! Transition curves are essential for driver comfort and safety.
Components of Simple Circular Curves
Unlock Audio Lesson
Now, let's discuss the various parts of a simple circular curve, such as tangent points and central angles. What do we know about tangent points?
They are the points where the curve touches the tangent lines.
Exactly right! We also have an intersection point where the two tangents meet. What is the significance of the angle of intersection?
It helps us understand how much the curve deviates from the tangents.
Correct! The angle of intersection plays a pivotal role in defining the curvature of the road. Lastly, how do we calculate the length of the curve?
By using the radius and the angle in radians, right?
That's right! Understanding these components is vital to the curve layout process.
Super-Elevation
Unlock Audio Lesson
Super-elevation is crucial in horizontal curves. Can someone tell me why we need it?
To counteract the centrifugal force acting on vehicles while turning!
That's absolutely correct, Student_2! Proper super-elevation reduces the risk of skidding. What factors do you think affect how much super-elevation is needed?
Speed of vehicles and road conditions, maybe?
Exactly! We always consider the expected speed and weather conditions when designing super-elevation.
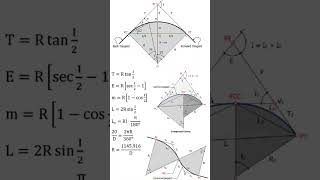
Computation of Curves
Unlock Audio Lesson
When setting out curves, various parameters must be calculated, such as tangent lengths and apex distances. Can anyone explain how we would find the tangent length?
By using the radius and the deflection angle?
Correct! The formula employs tangent calculations based on these parameters. How does this help us in a real-world scenario?
It helps ensure that the curves are safely navigable for vehicles!
Exactly! Correct calculations ensure smooth transitions on our roads.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on horizontal and vertical curves necessary for road and railway design. It classifies different types of curves, such as simple, compound, reverse, and transition curves, and details their components, computations, and the critical role of super-elevation in ensuring smooth vehicle movement.
Detailed
Curves in Transportation Engineering
In road and railway design, curves play a pivotal role in ensuring safe and efficient movement by accommodating direction and slope changes. This section delves into:
- Types of Curves: Learning about horizontal (e.g., simple, compound, reverse, transition) and vertical curves, which facilitate gradual direction changes.
- Curve Components: Understanding elements like tangents, intersections, tangent lengths, and apex distance that are essential for curve layout.
- Super-elevation: Highlighting its necessity in horizontal curves to counterbalance lateral forces and enhance vehicle stability.
- Computation: Exploring the relationships for calculating various parameters essential for setting out curves in the field, underpinning the application of geometry and trigonometry in practical situations.
- Practice Resources: A plethora of problems is provided for practice, encouraging problem-solving and a deep understanding of curve layout essentials.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Curves
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Curves are regular bends provided in the lines of communication, like highways, railways, etc., to make gradual change in the horizontal and vertical directions. Those curves that change the alignment or direction are known as horizontal curves, and those that change the slope are called vertical curves. Horizontal curves are provided in the horizontal plane to have the gradual change in direction, whereas vertical curves are provided in the vertical plane to obtain the gradual change in the grade.
Detailed Explanation
Curves are essential features in roads and railways, allowing smooth transitions in direction and slope. Horizontal curves help vehicles change direction without jerking or sudden turns, while vertical curves manage changes in elevation, ensuring a smoother ride. Think of a roller coaster—without curves, the ride would be abrupt and potentially unsafe as vehicles would have to turn sharply or climb steeply without any assists.
Examples & Analogies
Imagine driving along a scenic road. If the road just kept going straight without any curves, it would feel less enjoyable and also be more dangerous when changing directions. Curves in the road, like gentle bends, ensure drivers can navigate without losing control.
Types of Horizontal Curves
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Circular curves are classified as: (i) Simple, (ii) Compound, (iii) Reverse, and (iv) Transition curves.
Detailed Explanation
Horizontal curves can be categorized based on their shape and configuration. A simple curve is a single arc connecting two straight lines. Compound curves consist of multiple arcs of different radii, whereas reverse curves are two arcs bending in opposite directions. Transition curves gradually connect straight paths to curves to minimize sudden forces on vehicles.
Examples & Analogies
Think of riding a bicycle. If you suddenly turned sharply, it would be jarring. But if the path had a gentle curve, you would navigate smoothly. A simple curve is like a smooth ramp; a compound curve is like a wavy path with slight dips and rises, and a transition curve feels like easing into a turn before hitting a curve.
Simple Curves Explained
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A simple curve consists of a single arc of a circle connecting two straights. It has the same radius throughout. The intersection point of the two straights is called the intersection or vertex point.
Detailed Explanation
A simple curve is defined as a curve that has a constant radius and connects two straight segments. The point where these two lines meet at the curve is known as the intersection point. This curve shape is crucial as it maintains a uniform change in direction, contributing to safety and comfort for drivers.
Examples & Analogies
Picture a racetrack. The simplest turns are the half-circular curves that allow your car to smoothly transition from straight to angled movement, providing consistency in speed and control.
Understanding Compound Curves
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A compound curve consists of two or more simple curves having different radii bending in the same direction and lying on the same side of the common tangent.
Detailed Explanation
Compound curves comprise two or more simple curves connected sequentially, each with its radius but bending in the same direction. This allows for a gradual adjustment in direction while accommodating the needs of the terrain. In project design, understanding how to implement compound curves is crucial for maintaining road safety and efficiency.
Examples & Analogies
Consider a spiral staircase. Each step has a curve to it, gently guiding you to the next step while keeping you in a gradual ascent instead of a straight vertical climb, which would be awkward and uncomfortable.
Reverse Curves Characteristics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A reverse curve is made up of two equal or different radii bending in opposite directions with a common tangent at their junction.
Detailed Explanation
Reverse curves are defined by their two arcs, which bend in opposite directions but share a tangent point. They are often used in situations where two straight paths are close, allowing for a seamless transition between them. However, they should be used cautiously in high-speed areas to minimize abrupt changes.
Examples & Analogies
Think of a race track with a sharp hairpin turn. One segment curves left, and immediately after, the next curves right. This design allows vehicles to navigate what could be a jarring shift between two straight paths.
Transition Curves Importance
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A transition curve is provided in between the straight line and circular curve to provide gradual centrifugal force.
Detailed Explanation
Transition curves serve to smooth the transition from a straight path to a curve by gradually introducing centrifugal forces. This gradual change allows vehicles to adjust their speed and maintain control without abrupt changes in inertia. Proper implementation of transition curves enhances safety and improves the driving experience.
Examples & Analogies
Think about when you're running and need to turn a corner. If you just suddenly change direction, you might stumble. But if you gradually lean into the turn, your body adapts, maintaining your balance and speed—this is the principle behind transition curves.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Types of Curves: Horizontal vs. Vertical curves help in geometry for roads and railways.
-
Components of Curves: Understand tangents, apex, central angles, etc.
-
Super-elevation: Critical for safe navigation through circular curves.
-
Computation: Essential for real-world applications in road layouts.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A simple curve in road design allows for smooth transitions at intersections.
-
Super-elevation reduces the risk of an accident by compensating for centrifugal forces on curves.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Curves in the road, turn left or right; with super-elevation, we speed without fright.
📖 Fascinating Stories
-
Imagine driving through a scenic landscape. Each curve represents a new adventure, but only if designed well can it be a smooth ride without less strain on the vehicle.
🧠 Other Memory Gems
-
C-H-S: Curvature leads to Horizontal, and Super-elevation for stability.
🎯 Super Acronyms
C.E.S.T
- Curvature
- Elevation
- Smoothness
- Transition – the keys to effective curves.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Horizontal Curve
Definition:
A curve affecting the alignment or direction in the horizontal plane.
-
Term: Vertical Curve
Definition:
A curve affecting the slope in the vertical plane.
-
Term: Superelevation
Definition:
The banking of a roadway at a curve to counteract centrifugal force.
-
Term: Tangent
Definition:
A straight line that touches a curve at a single point.
-
Term: Apex
Definition:
The highest point or midpoint of a curve.
-
Term: Compound Curve
Definition:
A combination of two or more simple curves with different radii.
-
Term: Back Tangent
Definition:
The tangent line before the curve.
-
Term: Forward Tangent
Definition:
The tangent line after the curve.