Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Instantaneous Velocity
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to explore instantaneous velocity. Who can tell me how average velocity differs from instantaneous velocity?
Average velocity is the total distance divided by the total time, but it doesn't show how fast something is moving at a specific moment!
Exactly! Average velocity provides an overall picture, but instantaneous velocity tells us the speed at any specific time. We calculate it by taking the limit of average velocity as the time interval approaches zero. Can anyone give me the formula for that?
I think itβs v = limit as Ξt approaches 0 of Ξx/Ξt!
Well done! And this gives us the instantaneous velocity at that instant. Remember, the smaller the Ξt, the closer we get to the true instantaneous velocity.
Can we visualize this on a graph?
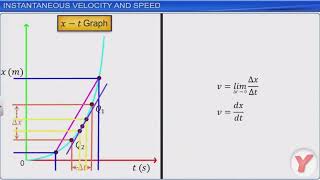
Great question! Imagine plotting a position vs. time graph. The instantaneous velocity is represented by the slope of the tangent line at any point. So, let's keep that in mind as we move forward.
Graphical Representation of Velocity
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
To understand how to find instantaneous velocity graphically, remember the concept of the tangent line. If I want to find the velocity at t=4s, what should I do?
You would draw a tangent line at that point on the graph?
Correct! This tangent lineβs slope gives us the instantaneous velocity at that specific moment. What happens if our Ξt is too large?
It would give us an average velocity instead of the instantaneous velocity!
Right again! Always remember that as Ξt approaches zero, we zero in on specific values of velocities. Itβs crucial for accurately interpreting motion.
Numerical Methods for Instantaneous Velocity
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs shift gears to how we can find instantaneous velocity numerically. What do we mean by calculating average velocities as we reduce the intervals?
We measure the change in position over smaller time intervals to see what value it approaches.
Exactly! For instance, if I calculated velocities for intervals of 2s, 1s, down to 0.01s, what would I expect to find?
The values will get closer and closer to the instantaneous velocity of the motion!
That's right! And when we plot these values, they should converge to a single point on our graph illustrating the instantaneous velocity.
Instantaneous Speed vs. Instantaneous Velocity
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs switch to speed now. How does instantaneous speed relate to instantaneous velocity?
Instantaneous speed is just the magnitude of the instantaneous velocity without considering direction, right?
Precisely! So if we have a velocity of +24 m/s or -24 m/s, the instantaneous speed is the same for both.
What about average speed? How does that relate to average velocity?
Great question! Average speed is always greater than or equal to the magnitude of average velocity. Why do you think that is?
Because average speed doesn't consider direction, so it adds all the distances together.
Exactly! And that's key to differentiating between these concepts.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Instantaneous velocity is defined as the limit of average velocity as the time interval approaches zero. It provides the velocity of an object at a specific moment. The section also discusses how both instantaneous velocity and speed are calculated, using graphical representation and numerical methods.
Detailed
Instantaneous Velocity and Speed
In this section, we delve into the concepts of instantaneous velocity and instantaneous speed. Average velocity provides the overall speed of an object over a specific time period, but it does not account for variations during that time. To determine how fast an object is moving at any instant, we focus on the instantaneous velocity (v), which is defined mathematically as:
$$v = \lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t}$$
This equation indicates that, as the time interval ($\Delta t$) becomes infinitesimally small, we can find the precise velocity at time (t). The graphically represented tangent line at a point on a position-time graph also conveys this concept.
To compute instantaneous velocity numerically, one can evaluate average velocities over progressively smaller intervals and observe the limiting value as $\Delta t$ trends to zero. The section concludes with the distinction between instantaneous velocity and instantaneous speed, emphasizing that while velocity can have a direction (positive or negative), speed is simply the absolute value of velocity.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Instantaneous Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The average velocity tells us how fast an object has been moving over a given time interval but does not tell us how fast it moves at different instants of time during that interval. For this, we define instantaneous velocity or simply velocity v at an instant t.
Detailed Explanation
Average velocity is calculated over a time interval; however, it doesn't give specific information about how fast an object is moving at any single momentβthis is where instantaneous velocity comes into play. Instantaneous velocity refers to the speed of an object at a specific point in time.
Examples & Analogies
Think of driving a car and looking at the speedometer. The speedometer shows your instantaneous velocity at that moment versus looking at a trip meter that shows the average speed over your entire journey.
The Concept of Limit
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The velocity at an instant is defined as the limit of the average velocity as the time interval βt becomes infinitesimally small.
Detailed Explanation
In calculus, to find the instantaneous velocity, we take the average velocity over smaller and smaller time intervals (βt). As βt approaches zero, we obtain a more precise measure of how fast the object is moving at that precise moment. This mathematical approach allows us to define instantaneous velocity accurately.
Examples & Analogies
Imagine measuring how fast a sprinter runs, but instead of running the full distance, you time how long it takes to cover increasingly smaller sections of the track. As you get closer to measuring one second, your reading becomes more accurate to their actual running speed at that exact moment.
Graphical Determination of Instantaneous Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We can use the equation for velocity at an instant either graphically or numerically.
Detailed Explanation
To find instantaneous velocity on a graph, you can consider the slope of the position-time graph at a particular point. The tangent line at that point provides the instantaneous velocityβthis slope reflects how steeply the line rises, indicating the object's speed at that instant.
Examples & Analogies
Imagine dropping a ball and watching its position over time on a graph. To find out exactly how fast it is falling at a certain moment (say, just after it has been dropped), you draw a tangent line at that point. The steeper the line, the faster the ball is falling at that moment.
Numerical Calculation of Instantaneous Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If we have data of positions at different instants or an exact expression for the position as a function of time, we can calculate βx/βt from the data for decreasing values of βt and find the limiting value.
Detailed Explanation
If we have a function that describes the position of an object over time, we can differentiate this function to find instantaneous velocity. Additionally, by calculating changes in position (βx) over very small changes in time (βt) repeatedly, we approach the velocity value accurately.
Examples & Analogies
Consider a runner's position over time given by a formula. By plugging in smaller and smaller time intervals in your calculations, you'd be narrowing down to the runner's exact speed at any given moment, much like calibrating a fine measurement tool to be more precise.
Understanding Speed
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Instantaneous speed or simply speed is the magnitude of velocity.
Detailed Explanation
While velocity includes direction, speed solely focuses on how fast an object is moving, disregarding the direction. For example, whether moving forward at +24.0 m/s or backward at -24.0 m/s, the speed remains 24.0 m/s.
Examples & Analogies
When measuring how fast a race car is going, you care about the number on the speedometer (the speed), not whether it's going forward or in reverse. This distinction is crucial, especially in physics.
Relation Between Average Speed and Instantaneous Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Though average speed over a finite interval of time is greater or equal to the magnitude of the average velocity, instantaneous speed at an instant is equal to the magnitude of the instantaneous velocity at that instant.
Detailed Explanation
Average speed measures the total distance traveled divided by total time, while average velocity considers the net displacement over the same time. The instantaneous measures, however, capture the speed and direction at particular instances. Therefore, instantaneous speed is always the absolute value of instantaneous velocity.
Examples & Analogies
If a car travels a curved path, its average speed might be high because it covers a long distance in a certain time, but its average velocity might be lower because it may end up not far from the starting point. Instantaneous measures give you the true pace at every fraction of the journey.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Instantaneous Velocity: Defined as the limit of average velocity as the time interval approaches zero.
-
Average Velocity: Calculated by dividing total displacement by total time for the interval.
-
Instantaneous Speed: The magnitude of instantaneous velocity, disregarding direction.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When an object's position is defined as a function of time, for example, x = a + btΒ², you can find instantaneous velocity by differentiating the function with respect to t.
-
In a position-time graph, the instantaneous velocity at t=4s can be found by calculating the slope of the tangent line at that point.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Instantaneous speed you see, is the motionβs pure decree.
π Fascinating Stories
-
Imagine a car speeding down a highway. At every moment, we capture how fast it's going without any delay, illustrating instantaneous velocity.
π§ Other Memory Gems
-
I See Instantaneous Void (ISIV) β for Instantaneous Speed vs. Instantaneous Velocity.
π― Super Acronyms
VAST - Velocity Always Shows Time (the essence of understanding instantaneous velocity).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Instantaneous velocity
Definition:
The velocity of an object at a specific instant in time, defined as the limit of average velocity as the time interval approaches zero.
-
Term: Average velocity
Definition:
The total displacement divided by the total time taken.
-
Term: Instantaneous speed
Definition:
The magnitude of instantaneous velocity, indicating how fast an object is moving regardless of direction.