Enrol to start learning
Reading is open to everyone. Enrolling is free, and it is what unlocks the audio lessons, practice tests and progress tracking.
5.5.2. Finding square root through repeated subtraction
Interactive Audio Lesson
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free account
Today, we're going to learn about how to find the square root of a number using repeated subtraction. Can anyone tell me what a square root is?
It's the number that, when multiplied by itself, gives the original number!
Very good! For instance, the square root of 25 is 5 because 5 times 5 equals 25. But today, we'll do this using a different method called repeated subtraction.
How does that work?
Great question! We start with a perfect square and keep subtracting odd numbers from it until we reach zero. Let's explore this with the number 81.
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free account
Let's take 81. We subtract 1, then 3, then 5. Who can remind me what the first few subtractions would look like?
81 minus 1 is 80, then minus 3 is 77!
Excellent! Keep going. What comes next?
So, 77 minus 5 is 72, and 72 minus 7 is 65.
Perfect! We keep doing this until we reach zero. Can someone finish this for 81?
If I keep subtracting, I get to 0 after 9 steps.
Correct! This means the square root of 81 is indeed 9. Well done!
Unlock the classroom podcast
The transcript is above and free to read. A free account plays the conversation back.
Create a free accountNow, why do you think we subtract odd numbers, specifically?
Maybe because every square number can be expressed this way?
Exactly! The sum of the first n odd natural numbers gives us n². That's why subtracting odd numbers is effective in reaching zero when we start with a square number.
So all perfect squares can be found using this method?
Yes! This illustrates the beautiful relationship in mathematics between squares and odd numbers. Let’s practice this method with more examples!
Overview
Short Summary
The section explains how to find square roots using the method of repeated subtraction of odd natural numbers.
Medium Summary
In this section, students learn that square roots can be found by subtracting consecutive odd natural numbers from a perfect square until reaching zero. This method demonstrates the relationship between square numbers and odd numbers.
Detailed Summary
Finding Square Roots through Repeated Subtraction
In this section, we explore a unique method to find the square root of a perfect square by utilizing the principle that the sum of the first n odd natural numbers equals n². By starting with a perfect square and subtracting successive odd numbers, we can ultimately derive the square root.
Key Concepts:
-
Repeated Subtraction: The process involves subtracting 1, 3, 5, 7, and so forth from the perfect square. The total number of subtractions made until the remaining value reaches zero gives the square root.
-
Example: Taking the number 81 as an example:
- 81 - 1 = 80
- 80 - 3 = 77
- 77 - 5 = 72
- 72 - 7 = 65
- 65 - 9 = 56
- 56 - 11 = 45
- 45 - 13 = 32
- 32 - 15 = 17
- 17 - 17 = 0
After 9 subtractions, we reach 0, thus confirming that the square root of 81 is 9.
-
The process of finding square roots through this method highlights the deeper relationship between square numbers and odd counting numbers, showcasing a remarkable property in mathematics.
Reference YouTube Videos
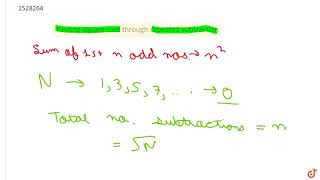
Audio Book
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountDo you remember that the sum of the first n odd natural numbers is n2? That is, every square number can be expressed as a sum of successive odd natural numbers starting from 1.
Detailed Explanation
The concept of square roots is closely related to square numbers. A square number is a number that can be expressed as the product of an integer with itself. For example, 4 (which is 2x2) and 9 (which is 3x3) are square numbers. The square root of a number is the value which, when multiplied by itself, gives the original number. For instance, the square root of 9 is 3 because 3 x 3 = 9.
Examples & Analogies
Think of a square garden. If you wanted to determine the size of one side based on the total area, you could visualize how many odd-length strips of fencing you would need to measure out. Each odd number corresponds to a specific step in defining the square's area.
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountConsider 81. Then, (i) 81 – 1 = 80 (ii) 80 – 3 = 77 (iii) 77 – 5 = 72 (iv) 72 – 7 = 65 (v) 65 – 9 = 56 (vi) 56 – 11 = 45 (vii) 45 – 13 = 32 (viii) 32 – 15 = 17 (ix) 17 – 17 = 0 From 81 we have subtracted successive odd numbers starting from 1 and obtained 0 at 9th step. Therefore 81 = 9.
Detailed Explanation
To find the square root of a number through repeated subtraction, you start with the number (like 81) and subtract successive odd integers (1, 3, 5, etc.) until you reach 0. The total number of times you subtract corresponds to the square root of the original number. Here, after subtracting 9 odd numbers from 81, we reach 0, indicating that the square root of 81 is 9.
Examples & Analogies
Imagine you have 81 apples, and each minute you remove sets of apples that gradually get larger (1 apple in the first minute, then 3 apples, then 5 apples, etc.). If you continue this until you have no apples left, the number of minutes it took represents the square root of how many apples you started with!
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free accountCan you find the square root of 729 using this method? Yes, but it will be time consuming. Let us try to find it in a simpler way.
Detailed Explanation
Finding square roots through repeated subtraction can be simple yet time-consuming for larger numbers like 729. Instead of subtracting repeatedly, we can use easier methods like prime factorization, which pairs up the prime factors of a number to find its square root effectively.
Examples & Analogies
Think about finding the number of rows and columns needed in a large garden. Instead of trial and error with a small count each time, using a systematic approach (like looking at dimensions) can save time and effort!
--
Key Concepts
Core takeaways and short definitions to help you quickly recall the key ideas from this section.
Repeated Subtraction: The process involves subtracting 1, 3, 5, 7, and so forth from the perfect square. The total number of subtractions made until the remaining value reaches zero gives the square root.
Example: Taking the number 81 as an example:
81 - 1 = 80
80 - 3 = 77
77 - 5 = 72
72 - 7 = 65
65 - 9 = 56
56 - 11 = 45
45 - 13 = 32
32 - 15 = 17
17 - 17 = 0
After 9 subtractions, we reach 0, thus confirming that the square root of 81 is 9.
The process of finding square roots through this method highlights the deeper relationship between square numbers and odd counting numbers, showcasing a remarkable property in mathematics.
Examples
Step-by-step examples to apply the section's ideas and test your understanding.
Example 1: Finding the square root of 81 by subtracting odd numbers and reaching 0 after 9 subtractions.
Example 2: If you start with 36 and use repeated subtraction: 36 - 1, 36 - 3, and so on, you will find that you will reach 0 after 6 steps.
Memory Aids
Interactive tools to help you remember key concepts
Flash Cards
Glossary
Square Root
A value that, when multiplied by itself, gives the original number.
Repeated Subtraction
A method of finding square roots by continuously subtracting odd numbers from a perfect square until zero is reached.
Odd Natural Numbers
The sequence of numbers that are not divisible by 2, e.g., 1, 3, 5, 7, etc.