Properties of Square Numbers
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Square Numbers
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Good morning, class! Today, we will be discussing square numbers. Who can tell me what a square number is?

Isn't it a number that can be expressed as the product of an integer with itself?

Exactly! For instance, 4 is a square number because it's 2 times 2. Now, can anyone share some more examples?

1, 9, 16, and 25! They all follow that pattern.

Great! Now, remember that square numbers like 1, 4, and 9 can be written as 1^2, 2^2, 3^2, and so on. A helpful acronym to remember this is ‘SQUAR’, which stands for Square Numbers = QUote A Result.

Is there a way to know if a number is a square just by looking at its last digit?

Good question! Yes, all square numbers end with the digits 0, 1, 4, 5, 6, or 9. So, if you see a number ending with 2, 3, 7, or 8, it can't be a square number!

That makes it easier to identify non-square numbers!

Indeed! Let’s recap: square numbers can be expressed as n^2, they have specific unit digits, and certain patterns can help us identify them.
Properties of Square Numbers
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s explore some interesting properties of square numbers. What can you tell me about the zeros at the end of square numbers?

They can only have an even number of zeros!

Correct! For example, 100 has two zeros, and 40000 has four zeros. If we look at an odd number like 25, it has no zeros at all. Now, how about the relationship between odd and even squares?

The square of an even number is even, and the square of an odd number is odd!

Exactly! Can anyone think of how can we visualize square numbers as patterns?

Like using dots to create a square shape?

Yes! And also, remember the sum of the first n consecutive odd numbers gives us n squared. This pattern is quite fascinating.

So, 1 + 3 + 5 adds up to 9, which is 3 squared!

Perfect! Now let’s summarize what we've learned about the properties of square numbers.
Real-World Applications
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

So far, we’ve covered the properties and concepts of square numbers. Can anyone think of where we might see square numbers in real life?

In architecture, when designing square spaces!

Excellent! And how about in calculating areas?

Yeah! The area of a square is found by squaring the length of one of its sides.

Exactly. If a garden has a side length of 5 m, the area is 5^2 = 25 m². Remember, understanding square numbers can help in various subjects, especially geometry.

What about when we're measuring things or trying to fit objects into spaces?

Great point! The concepts of square numbers are foundational in measurements, design, and various fields in mathematics.

So recognizing these patterns can help us in solving problems more effectively!

Exactly! Always keep an eye out for square numbers! In summary, we've discussed how square numbers appear in multiple contexts.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore square numbers, including their properties regarding their units digits, the zeros at the end of square numbers, and various methods to determine their nature. We also delve into interesting patterns related to square numbers that emerge through mathematical operations.
Detailed
Properties of Square Numbers
Square numbers are integers that can be expressed as the product of an integer with itself. For example, 1, 4, 9, and 16 are all square numbers because they can be expressed as 1x1, 2x2, 3x3, and 4x4 respectively. In this section, we will explore several key properties of square numbers:
Key Properties:
- Unit's Digits: All square numbers end with the digits 0, 1, 4, 5, 6, or 9. Knowing this helps identify non-square numbers quickly—if a number ends with 2, 3, 7, or 8, it cannot be a square number.
- Even Number of Zeros: Square numbers can only have an even number of zeros at the end. For instance, the squares of numbers like 10 and 100 have two and four zeros, respectively.
- Nature of Odd and Even Squares: The square of an even number is always even, whereas the square of an odd number is always odd.
- Sum of Odd Numbers: The square of a natural number can also be represented as the sum of the first n odd numbers, i.e., 1 + 3 + 5 = 9 (which is 3^2).
Patterns:**
Examining the differences between consecutive square numbers reveals patterns in the number of non-square integers present between them. For example, between squares n^2 and (n+1)^2, there are 2n non-square numbers, which can be deduced by simple arithmetic.
This section serves as a foundation for understanding square numbers, their behaviors, and their importance in algebra and geometry.
Youtube Videos








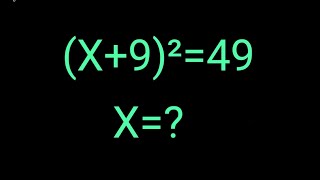

Audio Book
Dive deep into the subject with an immersive audiobook experience.
Squares of Numbers from 1 to 20
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Following table shows the squares of numbers from 1 to 20.
| Number | Square |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
| 11 | 121 |
| 12 | 144 |
| 13 | 169 |
| 14 | 196 |
| 15 | 225 |
| 16 | 256 |
| 17 | 289 |
| 18 | 324 |
| 19 | 361 |
| 20 | 400 |
Detailed Explanation
This chunk presents a table displaying the numbers from 1 to 20 along with their corresponding squares. The left column lists natural numbers, and the right column represents the calculated squares of these numbers. For example, the square of 3 is 9 (since 3 × 3 = 9), the square of 4 is 16 (4 × 4 = 16), and so forth up to 400 (20 × 20). Students can clearly see the relationship between a number and its square.
Examples & Analogies
Imagine stacking squares of different sizes. Each number represents a square's side length, and its square represents how many unit squares can fit inside. So, if you have a square that is 4 units long on each side, you can fit 16 smaller squares (4 × 4) inside it!
Ending Digits of Square Numbers
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Study the square numbers in the above table. What are the ending digits (that is, digits in the units place) of the square numbers? All these numbers end with 0, 1, 4, 5, 6 or 9 at units place. None of these end with 2, 3, 7 or 8 at unit’s place.
Detailed Explanation
Here, we analyze the units digit (or the last digit) of square numbers derived from the earlier table. It notes that square numbers (like 1, 4, 9, 16, 25) exclusively end with certain digits – specifically 0, 1, 4, 5, 6, or 9. This means if we see any number ending in 2, 3, 7, or 8, we can confidently conclude that it is not a square number. For example, 25 (which ends with 5) is a square number, while 22 (which ends with 2) cannot be a square.
Examples & Analogies
Think of square numbers as special tickets for a concert that only have specific ending numbers. If your ticket ends in 2, your entry is denied because it's not one of the lucky numbers. However, if it ends in 0, 1, or 5, you're set to go!
Even and Odd Square Numbers
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
What can you say about the squares of even numbers and squares of odd numbers?
Detailed Explanation
This section encourages the exploration of patterns in squares of even and odd numbers. It hints that all squares derived from even numbers remain even (like 2² = 4, 4² = 16), while squares from odd numbers result in odd outcomes (like 3² = 9, 5² = 25). The squared outcomes correspond to the nature of the original numbers: evens yield evens, and odds yield odds.
Examples & Analogies
Imagine baking cakes: if you mix an even number of eggs together (like 2 or 4), your batter will always have an even amount. On the other hand, if you use an odd number of eggs (like 3 or 5), your batter will have an odd amount. This represents how squares behave with even and odd numbers!
Perfect Squares Identified
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Is 32 a square number? We know that 52 = 25 and 62 = 36. If 32 is a square number, it must be the square of a natural number between 5 and 6. But there is no natural number between 5 and 6. Therefore 32 is not a square number.
Detailed Explanation
This chunk delves into identifying whether a specific number, 32, is a perfect square. It explains that since 32 falls between the squares of 5 (25) and 6 (36), and there’s no whole number between 5 and 6, it confirms that 32 cannot be expressed as the square of a natural number. Thus, it is not a square number.
Examples & Analogies
Think of climbing stairs: if you can step one step at a time (like natural numbers), you can only reach specific heights. Since you can't step halfway (between levels 5 and 6), you can't reach a height of 32 with whole steps — hence, 32 is not a valid square height.
Conclusion of Square Numbers
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The following square numbers end with digit 1. Write the next two square numbers which end in 1 and their corresponding numbers.
| Square Number |
|---|
| 1 |
| 81 |
| 121 |
| 361 |
| 441 |
Detailed Explanation
Finally, this section asks students to identify square numbers ending in 1 and find subsequent examples. It highlights the tendency of certain square numbers to end with 1, encouraging pattern recognition among numbers such as 1, 121, and 361. This enhances students' understanding of numerical patterns and relationships between numbers.
Examples & Analogies
Picture a treasure hunt: imagine markers leading to treasures are placed in a specific pattern. When you find treasures with 1 as the ending digit, it's like uncovering hidden gems of knowledge. You get to explore which numbers follow suit, quite like finding the next clues on a trail!
Key Concepts
-
Square Numbers: Integers expressed as n^2.
-
Units Digit: Digit in the ones place; for squares, it’s limited to specific digits.
-
Perfect Squares: Another name for square numbers, emphasizing their integrity.
-
Even Zeros: Square numbers terminate with even zeros.
-
Odd and Even Squares: The parity of the original number reflects in its square.
Examples & Applications
Example 1: The square of 5 is 25, i.e., 5^2 = 25.
Example 2: The square of a number ending with 5, like 25, gives a square ending in 25.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In a square, we take a side, Multiply it by itself, and watch it glide.
Stories
Once in a math kingdom, the numbers met, The squares always played last, in sun's warm set. They danced only with 0, 1, 4, 5, 6 and 9, Because those were their friends; the perfect, so fine!
Memory Tools
To remember square endings, just recall: '0, 1, 4, 5, 6, and 9 stand tall'.
Acronyms
Remember SQUARE for Square numbers
Sidelengths of units in Quadrants Are Real Equally!
Flash Cards
Glossary
- Square Number
A number that can be expressed as the product of an integer with itself.
- Perfect Square
Another term for square numbers, emphasizing their nature as integers.
- Units Digit
The digit in the ones place of a number.
- Even Number of Zeros
Refers to square numbers having an even count of trailing zeros.
Reference links
Supplementary resources to enhance your learning experience.
