Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Addition and Subtraction of Algebraic Expressions
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's start by discussing how we can add and subtract algebraic expressions. Does anyone remember what an algebraic expression is?
An algebraic expression is made up of variables and constants, like x + 3 or 2y β 5.
Exactly! Now, when we add expressions like 7xΒ² - 4x + 5 and 9x - 10, how should we organize them?
We should write like terms in the same column!
Well done! This helps us combine them efficiently. Letβs look at the terms together.
So, -4x + 9x equals 5x?
Right! Now, can anyone summarize the steps we've discussed?
We organize like terms, add or subtract them, and write down the final expression!
Perfect! Remember the acronym LATE: Like terms, Add or subtract, Then write the final expression.
Multiplication of Algebraic Expressions
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's move on to multiplication. Can someone explain what a monomial is?
A monomial is an algebraic expression that contains only one term, like 3xy.
Exactly! Now, how do we multiply two monomials, say 4x and 5y?
We multiply the coefficients and then the variables, so it becomes 20xy.
Great! And what happens when we multiply a monomial by a polynomial?
We distribute the monomial to each term of the polynomial.
Yes! This is called using the distributive property. Who can give me an example?
If we multiply 3x by (4x + 5), we get 12xΒ² + 15x.
Exactly correct! Remember to watch out for like terms when simplifying.
Understanding Polynomial Multiplication
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that weβve discussed monomials, letβs look at binomials. What is a binomial?
A binomial is an algebraic expression with two terms, like x + 2.
Yes! How do we multiply two binomials, such as (x + 3) and (x - 2)?
We use the distributive property for each term in the first binomial with each term in the second binomial.
Exactly! So, what do we get when we multiply them?
We get xΒ² + 3x - 2x - 6, which simplifies to xΒ² + x - 6.
Correct! Always remember to combine like terms in the end.
Can we use a mnemonic for this? Like βGreet, Multiply, and Simplifyβ?
Thatβs a wonderful idea! It makes it easier to remember the process.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section covers key operations involving algebraic expressions, such as addition, subtraction, and multiplication of monomials and polynomials. It also highlights the importance of identifying like terms, using the distributive property, and understanding algebraic identities.
Detailed
In this section, we dive into algebraic expressions, which are mathematical phrases that can include constants, variables, and operations. The focus is on how to add and subtract these expressions by combining like terms effectively. Importance is placed on writing expressions in a structured format to visualize the calculations clearly. Moreover, we explore the multiplication of monomials and the rules that apply, including how to handle multiple terms systematically using the distributive property. The section emphasizes that algebraic identities can simplify calculations and provide deeper insights into mathematical relationships between expressions.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Algebraic Expressions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In earlier classes, we have already become familiar with what algebraic expressions (or simply expressions) are. Examples of expressions are: x + 3, 2y β 5, 3xΒ², 4xy + 7 etc.
Detailed Explanation
Algebraic expressions involve variables, constants, and operations. A variable is a symbol (like x or y) that can represent a number. A constant is a fixed number (like 3 or 5). An expression combines these elements using operations like addition, subtraction, and multiplication. The examples provided help illustrate different forms of these expressions: single variables, terms with coefficients, and combinations of variables and constants together.
Examples & Analogies
Think of algebraic expressions like shopping lists. If 'x' represents the number of apples and 'y' represents oranges, 'x + 3' could mean buying 'x' apples and 3 bananas. Just like changing the number of items changes your expense, changing variables in expressions alters their value.
Addition of Algebraic Expressions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For example, to add 7xΒ² β 4x + 5 and 9x β 10, we do:
7xΒ² β 4x + 5
+ 9x β 10
= 7xΒ² + 5x β 5.
Detailed Explanation
To add algebraic expressions, align like terms vertically. Like terms share the same variable part; for instance, the terms 'β4x' and '9x' are like terms. You can add the coefficients directly: β4 + 9 = 5, yielding '5x'. The process is similar for constants: 5 + (β10) results in β5. The final expression combines all simplified terms.
Examples & Analogies
Imagine combining two different fruit baskets. If one basket has '7 apples', '4 bananas', and '5 oranges', and the other has '9 bananas' and '10 oranges', you would add your apples separately from your bananas and oranges to see what you have in total.
Subtraction of Algebraic Expressions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Solution: 7xΒ² β 4xy + 8yΒ² + 5x β 3y
β (5xΒ² β 4yΒ² + 6y β 3)
= 2xΒ² β 4xy + 12yΒ² + 5x β 9y + 3.
Detailed Explanation
Subtraction in algebraic expressions also involves aligning like terms and carefully managing signs. Each term from the second expression (the one being subtracted) needs its sign changed according to the subtraction operation. For example, subtracting +5xΒ² switches it to β5xΒ². This change must then be combined with the first expression's terms. Collect similar terms to form the final expression.
Examples & Analogies
Imagine you have a certain number of fruits, and you give some away. If you have '7 bananas' but give away '5 bananas', to find out how many bananas you have left, visualize '7' and 'β5' being added, which results in '2 bananas'. The signs represent whether you have or lose items.
Multiplication of Algebraic Expressions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We shall look at the multiplication of two monomials. An expression that contains only one term is called a monomial.
Example: 4 Γ (3x) = 12x.
Detailed Explanation
Multiplying monomials involves simple arithmetic on their coefficients and applying the rules for exponents on variable parts. For example, multiplying '4' (a coefficient) by '3x' (a monomial) gives '12x'. Similarly, x multiplied by x (x^1 * x^1) becomes xΒ² due to the exponent rule which states to add exponents.
Examples & Analogies
Think of monomials as individual fruit trees. If one tree produces '4 fruits' and you have '3 trees', the total fruit is like multiplying, resulting in '12 fruits'. Each tree contributes to the total yield just like each term contributes in an expression.
Multiplication of a Monomial by a Polynomial
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Expression that contains two terms is called a binomial. Multiplying a monomial by a binomial, e.g., 3x Γ (5y + 2) results in 15xy + 6x.
Detailed Explanation
When multiplying a monomial by a binomial, distribute the monomial to each term in the binomial. For 3x Γ (5y + 2), you multiply 3x by both 5y and 2 individually. The process involves adhering to the distributive property, ensuring that each multiplication occurs which helps combine terms efficiently.
Examples & Analogies
Consider a scenario where you pay for two different items in a shop. If you spend '3 dollars' on '5 apples' and '2 oranges', you would calculate your total cost separately by multiplying your purchase amount with quantities. The way your money is distributed relates closely to how we distribute terms in an expression.
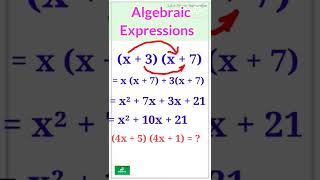
Multiplying a Polynomial by a Polynomial
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In multiplication of polynomials with polynomials, we should always look for like terms if any, and combine them.
Example: (2a + 3b) Γ (3a + 4b) = 6aΒ² + 17ab + 12bΒ².
Detailed Explanation
Multiply each term in one polynomial by every term in the other polynomial. This involves careful multiplication, followed by the need to combine like terms. For instance, in the product of polynomials (2a + 3b) and (3a + 4b), you multiply 2a with both 3a and 4b, and 3b with both, and finally sum all resulting terms while combining any like terms.
Examples & Analogies
If you have two types of plants (letβs say '2 types of apple trees' and '3 types of orange trees') and each type can produce different varieties, the combinations of each type teaching show how many varieties can be created, reflecting how polynomial terms interact, leading to a diverse range of results.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Algebraic Expressions: Formed from variables and constants.
-
Addition and Subtraction: Involves combining like terms.
-
Multiplication: Includes the distributive property for expanding expressions.
-
Polynomials: Comprised of one or more terms; can be of any degree.
-
Identities: Relationships between expressions that hold true universally.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: For the expression 7x + 5 - 2x, combine like terms to get 5x + 5.
-
Example 2: Multiply (x + 2)(x + 3) using distribution to get xΒ² + 5x + 6.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
When you add terms in a line, like terms together, itβs just fine!
π Fascinating Stories
-
Imagine a farmer named Polly who loves to multiply seeds. When she plants 3 rows of 2x plants, she joyfully watches 6x grow, adding fruits to her baskets!
π§ Other Memory Gems
-
Remember: 'Demon means distribute!' for using the distributive property.
π― Super Acronyms
Use the acronym *SIM* for Simplifying Expressions
- Simplify
- Identify and Multiply!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Algebraic Expression
Definition:
A mathematical phrase that can include numbers, variables, and operations.
-
Term: Monomial
Definition:
An algebraic expression that contains only one term.
-
Term: Binomial
Definition:
An algebraic expression that consists of two terms.
-
Term: Polynomial
Definition:
An algebraic expression made up of one or more terms.
-
Term: Like Terms
Definition:
Terms that have the same variable raised to the same power.
Challenge
- Question:
- Answer: No answer provided
- Hint: Expand step by step.
- Question:
- Answer: No answer provided
- Hint: Distribute first then combine like terms.