Learn
Games

4.3.2 - Equally likely outcomes

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Understanding Random Experiments

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Today, we're going to explore random experiments. Can anyone tell me what they think a random experiment is?

Student 1
Student 1

Is it something where you don't know the outcome?

Teacher
Teacher

Exactly! A random experiment is an experiment where the outcome cannot be predicted with certainty. For example, tossing a coin is a random experiment.

Student 2
Student 2

What can happen when we toss a coin?

Teacher
Teacher

Great question! When we toss a coin, we can get either heads or tails. These are the outcomes of our random experiment.

Equally Likely Outcomes

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Now let's talk about equally likely outcomes. What does it mean if the outcomes are equally likely?

Student 3
Student 3

Does it mean they have the same chance of happening?

Teacher
Teacher

Exactly! In a fair coin toss, both heads and tails have a probability of 1/2. Would someone like to calculate the probability of getting tails?

Student 4
Student 4

It’s also 1/2, right?

Teacher
Teacher

Spot on! When all outcomes are equally likely, we can express this mathematically as the number of favorable outcomes divided by the total number of outcomes.

Practical Examples

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

What do you think the possible outcomes are when we roll a die?

Student 1
Student 1

The numbers from 1 to 6!

Teacher
Teacher

Right! And since it's a fair die, what's the probability of rolling a 3?

Student 2
Student 2

It’s 1/6 because there are six outcomes!

Teacher
Teacher

Good job! This means for any number on the die, the probability remains the same. Now, what happens if we roll the die many times?

Student 3
Student 3

The counts would be closer to each other for each number?

Teacher
Teacher

Correct! They will converge towards their expected values as the number of rolls increases.

Linking Outcomes to Events

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Let’s connect outcomes to events. If I say getting a head is an event, what does that mean?

Student 4
Student 4

It’s one possible result of the toss?

Teacher
Teacher

Exactly! And there are other events like getting tails too. So what would be the probability of getting an even number when rolling a die?

Student 1
Student 1

There are three even numbers: 2, 4, and 6. So it would be 3 out of 6, or 1/2.

Teacher
Teacher

Perfect! Understanding events helps us link concepts together in probability.

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

The section discusses the concept of equally likely outcomes in probability, where each outcome in a random experiment has the same likelihood of occurring.

Standard

This section explores how equally likely outcomes arise in random experiments, illustrated with examples such as tossing a coin or rolling a die. It highlights how the probability of specific outcomes can be calculated based on their equal likelihood.

Detailed

Equally Likely Outcomes

In probability, an experiment can yield outcomes that are said to be equally likely when each outcome has an identical chance of occurring. For example, when tossing a coin, the results can be either Head or Tail, each with a probability of

\[ P(Head) = P(Tail) = \frac{1}{2} \]

Similarly, when rolling a fair die, each number from 1 to 6 has the same probability:

\[ P(n) = \frac{1}{6}, \text{ for } n = 1, 2, 3, 4, 5, 6 \]

As more repetitions of an experiment are performed, the results tend to stabilize around their expected probabilities. The section illustrates how conducting a larger number of tosses results in counts of heads and tails that tend to converge, indicating that these outcomes are equally likely. The concept is foundational in linking the practical outcomes of random experiments to the theoretical framework of probability.

Youtube Videos

Class-8-Maths-Ch-4-Data Handling-Topic- What are Equally Likely Events Tossing a Coin
Class-8-Maths-Ch-4-Data Handling-Topic- What are Equally Likely Events Tossing a Coin
Equally likely Outcomes | Data Handling | Chapter 5 Class 8 NCERT DATA HANDLING |
Equally likely Outcomes | Data Handling | Chapter 5 Class 8 NCERT DATA HANDLING |
Class 8 Chapter 4 Data Handling Guaranteed Qs in Exam 2025 #shorts #maths #class8
Class 8 Chapter 4 Data Handling Guaranteed Qs in Exam 2025 #shorts #maths #class8
Probability Of Rolling Dice | How To Calculate Dice Probabilities #Shorts #NowWeKnow
Probability Of Rolling Dice | How To Calculate Dice Probabilities #Shorts #NowWeKnow
Chances and Probability - Data Handling | Class 8 Mathematics Chapter 4 | CBSE 2024-25
Chances and Probability - Data Handling | Class 8 Mathematics Chapter 4 | CBSE 2024-25
Chance and Probability Class 8 Maths (Concept + Questions) - Data Handling | BYJU'S - Class 8
Chance and Probability Class 8 Maths (Concept + Questions) - Data Handling | BYJU'S - Class 8
Data Handling in One Shot | Maths - Class 8th | Umang | Physics Wallah
Data Handling in One Shot | Maths - Class 8th | Umang | Physics Wallah
12in Pizza vs 8in Pizza #ytshorts #ytshorts #mathsclass10 #ncert #byjus
12in Pizza vs 8in Pizza #ytshorts #ytshorts #mathsclass10 #ncert #byjus
#Maths #Maths shorts#Shorts#Video trending #data Handling #
#Maths #Maths shorts#Shorts#Video trending #data Handling #
Chance and probability related to real life : Data Handling Class 8 Maths NCERT Chapter 5
Chance and probability related to real life : Data Handling Class 8 Maths NCERT Chapter 5

Audio Book

Dive deep into the subject with an immersive audiobook experience.

Coin Toss Experiment

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

A coin is tossed several times and the number of times we get head or tail is noted. Let us look at the result sheet where we keep on increasing the tosses:

Number of tosses Tally marks (H) Number of heads Tally mark (T) Number of tails
50 | | | | | | | | | | | | 27 | | | | | | | | | | | | 23
| | | | | | | | | | | | | | | | |
60 | | | | | | | | | | | | 28 | | | | | | | | | | | | 32
| | | | | | | | | | | | | | | | | | | | | | | | |
70 ... 33 ... 37
80 ... 38 ... 42
90 ... 44 ... 46
100 ... 48 ... 52

Detailed Explanation

In this chunk, we observe the outcomes of a coin toss experiment where we count the frequency of heads and tails as we increase the number of times the coin is tossed. The tally marks show how often heads (H) and tails (T) are obtained over multiple tosses. For instance, after 50 tosses, we recorded 27 heads and 23 tails. The pattern continues as we toss the coin more, and it becomes evident that the number of heads and tails tends to get closer as we increase tosses, suggesting each outcome has an equal probability.

Examples & Analogies

Imagine flipping a coin while playing a game. At first, you might notice that heads come up more. But if you keep playing for a long time, you'll find that heads and tails balance out. This is similar to how more trials of the experiment lead to equal outcomes.

Equally Likely Outcomes

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Observe that as you increase the number of tosses more and more, the number of heads and the number of tails come closer and closer to each other. This could also be done with a die, when tossed a large number of times. Number of each of the six outcomes become almost equal to each other. In such cases, we may say that the different outcomes of the experiment are equally likely.

Detailed Explanation

As we continue to increase the number of tosses, the frequency of heads and tails will eventually balance out, indicating that both outcomes are equally likely. This principle applies not only to coin tossing but also to other random experiments like rolling a die. If we roll a die multiple times, we should expect to see roughly the same number of each outcome (1 through 6) after a sufficient number of rolls. This balance assures us that each side of the dice has an equal chance of landing face up, symbolizing 'equally likely outcomes.'

Examples & Analogies

Think of a fair six-sided die. You might roll it and get a 3 a few times in a row, but as you roll it more times, you will also see the numbers 1, 2, 4, 5, and 6 appear frequently, showing that all sides are equally likely to come up in the long run.

Linking Chances to Probability

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

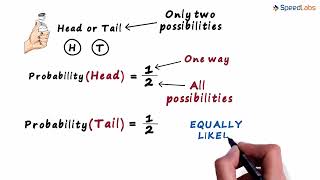
Consider the experiment of tossing a coin once. What are the outcomes? There are only two outcomes – Head or Tail. Both the outcomes are equally likely. Likelihood of getting a head is one out of two outcomes, i.e., (1/2). In other words, we say that the probability of getting a head = (1/2). What is the probability of getting a tail?

Detailed Explanation

When we toss a coin, we can only get two possible outcomes: Head (H) or Tail (T). Since both outcomes are equally likely, the probability of getting a head is 1 out of the 2 possible outcomes, which is mathematically expressed as 1/2. Similarly, the probability of getting a tail is also 1/2. This ratio implies that if we were to determine the likelihood of obtaining heads or tails, each has a 50% chance of occurring.

Examples & Analogies

Consider a simple scenario where you and a friend decide to flip a coin at the same time. If you both call 'heads,' you have a fair chance of winning; however, if you repeatedly flip the coin, you would expect to see heads and tails come up with similar frequency, promoting the idea of equal chances.

Outcomes as Events

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Each outcome of an experiment or a collection of outcomes makes an event. For example in the experiment of tossing a coin, getting a Head is an event and getting a Tail is also an event.

Detailed Explanation

In probability, every result from an experiment can be classified as an event. In the coin toss example, each side of the coin represents a distinct event: getting Heads is one event, and getting Tails is another event. Additionally, combined outcomes also represent events. For instance, getting either Heads or Tails from a single toss collectively represents the entire sample space of the experiment.

Examples & Analogies

Picture a game where you're drawing a colored ball from a bag. If you draw a red ball, that's one event, while drawing a blue ball is another. Both events represent different outcomes from your action of drawing.

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Random Experiment: An experiment with uncertain outcome.

  • Equally Likely Outcomes: Outcomes that have an equal chance of occurring.

  • Probability: A numerical expression of how likely an outcome is.

  • Event: A specific result or a set of results from an experiment.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • Tossing a coin yields two outcomes: heads or tails, each with a probability of 1/2.

  • Rolling a die has six equally likely outcomes: 1, 2, 3, 4, 5, and 6.

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • When you toss a coin, don't you see? Heads or tails, that's the key!

📖 Fascinating Stories

  • Imagine a fair game where coins and dice roll, each side has a fair chance, that's the goal!

🧠 Other Memory Gems

  • For outcomes, use the acronym 'ELO', which stands for 'Equally Likely Outcomes'.

🎯 Super Acronyms

Use the acronym 'P.O.E.' for Probability Outcomes Equally.

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: Random Experiment

    Definition:

    An experiment whose outcome cannot be predicted with certainty.

  • Term: Equally Likely Outcomes

    Definition:

    Outcomes of an experiment that have the same probability of occurring.

  • Term: Event

    Definition:

    A specific outcome or a collection of outcomes from an experiment.

  • Term: Probability

    Definition:

    A measure of the likelihood of a particular outcome occurring, ranging from 0 to 1.