Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Large Numbers with Exponents
Unlock Audio Lesson

Today, we're exploring exponents, a powerful tool for expressing large numbers. For example, instead of writing the mass of the Earth as 5,970,000,000,000,000,000,000,000 kg, we can write it as 5.97 × 10²⁴ kg. Can anyone tell me why this is beneficial?

It's easier to read and write!

Exactly! By using exponents, we can quickly understand the magnitude of the number. Now, let's look at how we represent smaller numbers using negative exponents.

What do you mean by negative exponents?

Good question! Negative exponents indicate division. For example, 10⁻² means 1 divided by 10 squared, or 0.01. Let’s practice converting 10⁻³.

So, that would be 1/1000, which is 0.001, right?

Correct! The pattern holds—each decrease in exponent decreases the value by a factor of ten. Let’s summarize: exponents allow us to express both very large and very small numbers efficiently.
Negative Exponents and Their Use
Unlock Audio Lesson

Now, let's dive into negative exponents a bit deeper. When we see expressions like 2⁻², what does that represent?

It’s like the reciprocal of 2 squared!

Exactly! 2⁻² = 1/(2²), which equals 1/4. It’s essential to remember that negative means we move into the denominator. Let’s calculate a few examples: what is 3⁻¹?

It’s 1/3!

Great! Remember, as you apply these concepts, try to state what each exponent signifies—this understanding is key to mastering the topic.
Converting Between Standard and Expanded Form
Unlock Audio Lesson

Now, let's shift gears and discuss how we can express numbers in expanded form using exponents. For example, how do we write the number 1425 using exponents?

We can break it down, right? It’s 1 × 10³ + 4 × 10² + 2 × 10¹ + 5 × 10⁰.

Exactly! Excellent work. Now, let’s apply this to a decimal number: how do we express 1425.36?

It would be 1 × 10³ + 4 × 10² + 2 × 10¹ + 5 × 10⁰ + 3 × 10⁻¹ + 6 × 10⁻²!

Perfect! That’s understanding the expanded form. Always remember, when you see a decimal, those negative exponents indicate the decimal placement.
Wrap-Up and Key Takeaways
Unlock Audio Lesson

To wrap up, we learned that exponents allow us to handle large and small numbers efficiently. Who can recap what negative exponents do?

Negative exponents show division, representing numbers less than one!

Exactly! And what about expressing numbers in expanded form? How is that useful?

It helps break down larger numbers or decimals to understand their values better!

Fantastic! Remember these concepts as we move forward into the laws of exponents and their applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The introduction covers the importance of exponents in simplifying large numbers, such as the mass of the Earth, and illustrates the concept of negative exponents with examples. It discusses how negative exponents represent fractions, aiding in calculations involving numbers less than one.
Detailed
Introduction to Exponents
Exponents are mathematical notations that allow us to express large numbers efficiently. For instance, the mass of the Earth is expressed using exponents as 5.97 × 10²⁴ kg instead of writing it out in full. In this section, we will explore the meaning of exponents, focusing on positive and negative integers.
We begin by reviewing how a number raised to a power represents repeated multiplication (e.g., 2⁵ = 2 × 2 × 2 × 2 × 2). We then delve into negative exponents, illustrating that an exponent like 10⁻² can be rewritten as 1/(10²), or
1/100, which equals 0.01. Through a series of patterns and examples, we learn how to compute values involving negative exponents and express numbers in expanded form. Understanding exponents is crucial in higher mathematics and helps simplify complex numerical situations.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Exponents
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Do you know?
Mass of earth is 5,970,000,000,000, 000, 000, 000, 000 kg. We have already learnt in earlier class how to write such large numbers more conveniently using exponents, as, 5.97 × 10²⁴ kg.
We read 10²⁴ as 10 raised to the power 24.
Detailed Explanation
Exponents are used to express large numbers in a more manageable way. For example, instead of writing the mass of the Earth as '5,970,000,000,000,000,000,000,000 kg', we can express it as '5.97 × 10²⁴ kg'. In this notation, '10' is the base and '24' is the exponent, indicating that we multiply 5.97 by itself 24 times.
Examples & Analogies
Imagine you have a really large crowd of people, like at a concert. If you want to tell someone how many people are there without counting each one, you might say 'there are approximately 50,000 people'. This is similar to how we use exponents to simplify large numbers; we summarize it rather than listing every individual.
Basic Understanding of Exponents
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We know 2⁵ = 2 × 2 × 2 × 2 × 2 and 2ᵐ = 2 × 2 × 2 × 2 × ... (m times). Let us now find what is 2⁼ 2 equal to?
Detailed Explanation
The expression '2⁵' means that the number 2 is multiplied by itself a total of 5 times. This is the essence of exponents - they help simplify multiplication of the same number. For instance, if we visualize the process, it becomes clearer: 2 × 2 = 4, then 4 × 2 = 8, continuing until we have multiplied 2 five times gives us 32. Additionally, when the exponent is zero, 2⁰ equals 1, a fundamental property of exponents.
Examples & Analogies
Think of exponents like a recipe. If your recipe calls for 2 cups of flour, multiplying that by 5 (2⁵) means you’re making a batch that requires much more flour! Similarly, if you forget to add any, it reminds you how crucial that step is.
Negative Exponents
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us now find what is 2⁻² equal to? Continuing the above pattern we get, 10⁻¹ = 1/10. As the exponent decreases by 1, the value becomes one-tenth of the previous value.
Detailed Explanation
Negative exponents indicate the reciprocal of the base raised to the absolute value of the exponent. For example, 2⁻² is equal to 1/(2²), which is 1/4. This shows that negative exponents effectively help us understand division or the concept of 'splitting' a number.
Examples & Analogies
Imagine you have a pizza divided into 4 slices. If you eat 1 slice (2⁻²), you're left with 3 slices, which means the remaining portion is less than what you initially had. This analogy highlights how reducing the exponent adds to our understanding of fractions.
Multiplicative Inverse
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In general, we can say that for any non-zero integer a, a⁻ᵐ = 1/aᵐ, where m is a positive integer. a⁻ᵐ is the multiplicative inverse of aᵐ.
Detailed Explanation
The multiplicative inverse refers to flipping the fraction, meaning a negative exponent inverts the base. This means if we have a number raised to a negative power, we can express it as a fraction. For instance, 5⁻¹ becomes 1/5, demonstrating that they are inversely related.
Examples & Analogies
Think of this like reversing a direction. If one way leads to a particular destination, the inverse (like going back) leads you to your original starting point. Similarly, a negative exponent takes you back to the starting point by flipping the value.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Exponents simplify the expression of large and small numbers.
-
Negative exponents represent the reciprocal of the base raised to the absolute value of the exponent.
-
The expanded form expresses numbers as the sum of their parts using powers of ten.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Mass of the Earth: 5,970,000,000,000,000,000,000,000 kg = 5.97 × 10²⁴ kg.
-
0.000007 m = 7 × 10⁻⁶ m; this translates into a very small number using negative exponents.
-
Converting 1425 to expanded form: 1 × 10³ + 4 × 10² + 2 × 10¹ + 5 × 10⁰.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Exponents are neat, they can’t be beat, powers of ten are simple and sweet.
📖 Fascinating Stories
-
Imagine a tiny ant representing a negative exponent; when the ant follows the pattern, it climbs down into the denominator.
🧠 Other Memory Gems
-
Remember, Negative means Divide: Just think of it as taking a number down to the basement, below one.
🎯 Super Acronyms
E.N.D. for Exponents, Negative, Divide - shows how exponents change numbers.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
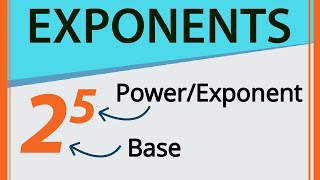
Term: Exponent
Definition:
A mathematical notation indicating the number of times a number (the base) is multiplied by itself.
-
Term: Negative Exponent
Definition:
An exponent indicating the reciprocal of the base raised to the absolute value of the exponent.
-
Term: Expanded Form
Definition:
A way of expressing a number as the sum of its individual digits multiplied by their place values.
-
Term: Base
Definition:
The number that is being raised to a power in an exponential expression.
-
Term: Multiplicative Inverse
Definition:
The reciprocal of a number; for example, the multiplicative inverse of 2 is 1/2.
