10 - HERON’S FORMULA

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Introduction to Heron's Formula

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Today, we are going to learn about Heron's Formula, a powerful tool for finding the area of triangles. Who can tell me what we normally need to calculate the area?

Student 1
Student 1

We usually need the base and the height.

Teacher
Teacher

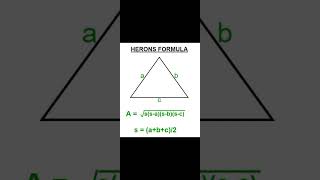
Exactly! But what if we don't know the height? That's where Heron's Formula comes in! It allows us to find the area using just the sides of the triangle. It’s stated as: Area = $$\sqrt{s(s-a)(s-b)(s-c)}$$, where s is the semi-perimeter.

Student 2
Student 2

How do we find the semi-perimeter?

Teacher
Teacher

Great question! The semi-perimeter s is calculated as $$s = \frac{a + b + c}{2}$$. Let's try calculating the semi-perimeter for a triangle with sides 40 m, 24 m, and 32 m.

Calculating Area Using Heron's Formula

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Now that we have s, how do we find the area?

Student 3
Student 3

We plug our values into the formula, right?

Teacher
Teacher

Yes! Remember, after calculating s, we also need to calculate $$s-a$$, $$s-b$$, and $$s-c$$. Can someone recall the lengths we were using?

Student 4
Student 4

The sides were 40 m, 24 m, and 32 m.

Teacher
Teacher

Perfect! Now, let's compute the area together step by step.

Real-World Applications of Heron's Formula

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Heron's formula is not just theoretical. It has several real-world applications! For instance, a triangular park will use this formula to calculate how much area there is for grass.

Student 1
Student 1

Can we see an example?

Teacher
Teacher

Sure! Let's take a triangular park with sides 120 m, 80 m, and 50 m. What do we do first?

Student 2
Student 2

Calculate the semi-perimeter!

Teacher
Teacher

Correct! Then we plug that into Heron's formula to calculate the area. It shows us how useful mathematics is in planning such parks!

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

Heron's formula provides a method to calculate the area of a triangle using the lengths of its sides.

Standard

Heron's formula allows us to calculate the area of a triangle when the height is unknown, using only the lengths of its sides. It involves calculating the semi-perimeter and subsequently applying the formula to find the area.

Detailed

In this section, we explore Heron's formula, which calculates the area of a triangle given the lengths of its three sides, denoted as 'a', 'b', and 'c'. The formula is expressed as:

$$
ext{Area} = \sqrt{s(s - a)(s - b)(s - c)
}
$$
where s is the semi-perimeter given by $$s = \frac{(a + b + c)}{2}$$. This formula is especially useful in cases where the height of the triangle is difficult to determine directly, making it a significant tool in geometrical calculations. We apply this formula through various examples and demonstrate its practicality in real-life scenarios.

Youtube Videos

Heron's Formula Class 9 in One Shot 🔥 | Class 9 Maths Chapter 10 Complete Lecture
Heron's Formula Class 9 in One Shot 🔥 | Class 9 Maths Chapter 10 Complete Lecture
Heron's Formula | Exercise 10.1 | Chapter 10 | SEED 2024-2025
Heron's Formula | Exercise 10.1 | Chapter 10 | SEED 2024-2025
Heron's Formula | Introduction | Chapter 10 | SEED 2024-2025
Heron's Formula | Introduction | Chapter 10 | SEED 2024-2025
Heron's Formula
Heron's Formula
Heron's Formula | One Shot | Class 9 Maths
Heron's Formula | One Shot | Class 9 Maths
Proof of Heron’s Formula | Class 9 Maths
Proof of Heron’s Formula | Class 9 Maths
Heron's Formula class 9
Heron's Formula class 9
Heron's Formula || class 9 || L-1🔥| By SUMAN SIR |🔥#SUMAN #SUMANSIR
Heron's Formula || class 9 || L-1🔥| By SUMAN SIR |🔥#SUMAN #SUMANSIR
Heron's Formula | Examples | Chapter 10 | SEED 2024-2025
Heron's Formula | Examples | Chapter 10 | SEED 2024-2025
Class - 9th, Maths Introduction Heron's Formula || maths ex 10 || maths class 9
Class - 9th, Maths Introduction Heron's Formula || maths ex 10 || maths class 9

Audio Book

Dive deep into the subject with an immersive audiobook experience.

Introduction to Heron's Formula

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

We know that the area of triangle when its height is given, is 1/2 × base × height. Now suppose that we know the lengths of the sides of a scalene triangle and not the height. Can you still find its area?

Detailed Explanation

This chunk introduces the concept of Heron's formula by discussing the traditional method of calculating the area of a triangle, which relies on knowing the height. However, in many cases, especially with scalene triangles where the heights are not easily calculable, knowing just the side lengths can still allow us to determine the area. Heron's formula offers a way to calculate the area using only the sides of the triangle.

Examples & Analogies

Imagine you're planning to build a triangular garden on your property. You have the lengths of all three sides but no idea how high the garden will be. Instead of trying to measure the height (which could be tricky), you can use Heron's formula to find out exactly how much space the garden will cover.

History of Heron

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Heron was born in about 10AD possibly in Alexandria in Egypt. He worked in applied mathematics. His works on mathematical and physical subjects are so numerous and varied that he is considered to be an encyclopedic writer in these fields. His geometrical works deal largely with problems on mensuration written in three books.

Detailed Explanation

This segment provides a brief biography of Heron, highlighting his contributions to mathematics and geometry. It illustrates that Heron was prolific in his writings and made significant developments in mensuration (the measurement of geometric figures). This background helps students appreciate the significance of Heron’s formula in the context of mathematical history.

Examples & Analogies

Think of Heron as an ancient mathematician who not only invented a formula but also laid the groundwork for many geometric principles we still use today. Just like how modern inventors create tools and technologies that change our ways of living, Heron's contributions have shaped our understanding of mathematics.

Definition and Application of Heron's Formula

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

The formula given by Heron about the area of a triangle is stated as: Area of a triangle = √(s(s-a)(s-b)(s-c)), where a, b and c are the sides of the triangle, and s = semi-perimeter, i.e., half the perimeter of the triangle = (a + b + c) / 2.

Detailed Explanation

Here we learn about the formula itself. The formula is expressed using constants derived from the triangle's dimensions. The 'semi-perimeter' (s) is crucial as it provides a way to relate the triangle's side lengths to its area. By knowing just the lengths of the sides, we can compute 's', 's-a', 's-b', and 's-c', and substitute these values into Heron's formula to find the area.

Examples & Analogies

Imagine having three sticks to make a triangle. You could rearrange these sticks but not know the height they form. Just like a complex recipe that requires specific ingredient combinations, the formula gives you a straightforward way to find the 'dish' — or the triangle's area — without needing all the details about the shape itself.

Example Calculation of Area

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Let us apply Heron's formula to calculate the area of the triangular park ABC, where a = 40 m, b = 24 m, c = 32 m. The semi-perimeter s is 48 m. Therefore, s – a = 8 m, s – b = 24 m, and s – c = 16 m. Area = √(48 × 8 × 24 × 16) m².

Detailed Explanation

This part provides a step-by-step calculation using an actual example of a park. We gather the lengths of the sides, calculate the semi-perimeter, and then substitute these values into Heron's formula. The result gives us the area of the triangle formed by the park, demonstrating practical usage of the formula.

Examples & Analogies

Consider this as a field project: you are asked to determine how much grass seed you need for the triangular area of your new park. Each stick represents a side you measure before using Heron's formula to easily compute the area without needing to visualize or calculate the height of that triangle.

Verification of Area by Different Methods

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

We check that the area calculated using Heron’s formula is the same as using the standard area formula for a right triangle, showing the consistency of mathematical principles.

Detailed Explanation

This section emphasizes the importance of verification. After calculating the area using Heron’s formula, we cross-check it against another method (in this case, the standard area formula for right triangles). Doing so shows that multiple methods can yield the same result, which strengthens our understanding of geometry.

Examples & Analogies

Think of this verification like double-checking your homework answers. Just as you would want to make sure your results are consistent across different math problems, validating that the area remains the same through various methods gives us confidence in our calculations.

Additional Examples

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Now using Heron’s formula, you verify this fact by finding the areas of other triangles, such as equilateral and isosceles triangles.

Detailed Explanation

This chunk encourages students to apply Heron's formula on different kinds of triangles, including equilateral and isosceles triangles. This practice illustrates that Heron’s formula is versatile and can be used broadly across various triangle types, reinforcing the student's understanding.

Examples & Analogies

Consider playing a game where you measure different triangular areas of different playground structures. By applying Heron's formula to each unique shape, you can uncover the hidden similarities and differences, just like discovering different patterns in nature.

Summary of Key Points

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

In this chapter, you have studied the following points: 1. Area of a triangle with its sides as a, b, and c is calculated by using Heron’s formula: Area of triangle = √(s(s-a)(s-b)(s-c)), where s = (a + b + c)/2.

Detailed Explanation

This final chunk provides a recap of the lessons learned in this section regarding Heron’s formula. Summarizing what they have covered allows students to consolidate their knowledge and facilitates review for exams or homework.

Examples & Analogies

Think of this summary like the key points at the end of a study session; it gives you a quick way to recall essential information about Heron’s formula, much like a cheat sheet that helps you prepare before a test.

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Heron's Formula: A method for calculating the area of a triangle given its side lengths.

  • Semi-Perimeter: The sum of the triangle's sides divided by two, needed for applying Heron's formula.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • {'example': 'Find the area of a triangle with sides 40 m, 32 m, and 24 m.', 'solution': 'Given $a=40$, $b=32$, $c=24$. The semi-perimeter $s = \frac{40 + 32 + 24}{2} = 48 m$. Then: \n$\text{Area} = \sqrt{48(48-40)(48-32)(48-24)} = \sqrt{48(8)(16)(24)} = \sqrt{24576} = 144 m^2.$'}

  • {'example': 'Find the area of an equilateral triangle with side 10 cm.', 'solution': 'Here, $a = b = c = 10$ cm. Calculate $s = \frac{10 + 10 + 10}{2} = 15$ cm. Then: \n$\text{Area} = \sqrt{15(15-10)(15-10)(15-10)} = \sqrt{15(5)(5)(5)} = \sqrt{375} = 5\sqrt{15} cm^2.$'}

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • To find the area, follow this way, / Semi-perimeter first, then area to display.

📖 Fascinating Stories

  • Imagine a park in the shape of a triangle. You want to plant flowers but need to know how much space you have. Using Heron's formula helps you calculate the area quickly!

🧠 Other Memory Gems

  • SAB: Semi-perimeter, Area, Base dimensions.

🎯 Super Acronyms

A = $$\sqrt{s(s-a)(s-b)(s-c)}$$, Remember

  • S: = Semi-perimeter.

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: Heron's Formula

    Definition:

    A mathematical formula that calculates the area of a triangle when the lengths of all three sides are known.

  • Term: SemiPerimeter

    Definition:

    Half the perimeter of a triangle, calculated as $$s = \frac{(a + b + c)}{2}$$.

  • Term: Area

    Definition:

    The measure of the space enclosed within a polygon.

  • Term: Scalene Triangle

    Definition:

    A triangle with all sides of different lengths.