10.2 - Summary

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Introduction to Heron's Formula

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Today, we are going to explore Heron's Formula, which allows us to calculate the area of a triangle when we only know the lengths of its sides. Can anyone tell me what those sides are typically called?

Student 1
Student 1

They are called side lengths, right?

Teacher
Teacher

Exactly! We denote the sides as a, b, and c. To compute the area, we also need a concept called the semi-perimeter, which is half the perimeter of the triangle.

Student 2
Student 2

How do we find the semi-perimeter?

Teacher
Teacher

Good question! We calculate it as $s = \frac{a + b + c}{2}$. Then we plug that into our formula for area.

Applying Heron's Formula

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Now that we have our semi-perimeter, let’s apply Heron's formula. Can anyone recall what the formula looks like?

Student 3
Student 3

Is it $\sqrt{s(s-a)(s-b)(s-c)}$?

Teacher
Teacher

Exactly right! We calculate the area by substituting our values for s, a, b, and c into that equation. Let's practice this with a triangle with sides 40 m, 32 m, and 24 m.

Student 4
Student 4

So, first, we find the semi-perimeter?

Teacher
Teacher

Yes, and then we apply them in the formula step-by-step!

Understanding the Importance of Heron's Formula

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Finally, why do you think knowing Heron's formula could be useful?

Student 1
Student 1

It helps in situations where measuring height might be hard, like in irregular land or parks!

Student 3
Student 3

And it helps in real-life applications like construction and landscaping.

Teacher
Teacher

Perfect! The formula is crucial for practical situations where conventional area calculations are not feasible.

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

This section introduces Heron's formula, providing a method to calculate the area of a triangle using its side lengths.

Standard

Heron's formula enables the calculation of the area of a triangle when only the lengths of its sides are known. It states that the area can be determined using the formula that incorporates the semi-perimeter of the triangle. This is particularly useful when the height is difficult or impossible to calculate.

Detailed

In this section, we delve into Heron's formula for calculating the area of a triangle given its three sides, denoted as a, b, and c. The formula is defined as:

$$ \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} $$

where $s$ is the semi-perimeter, calculated as $s = \frac{a+b+c}{2}$. This section highlights the applicability of Heron's formula in scenarios where determining the triangle's height is complex. Various examples, including triangles of different shapes and ratios, illustrate the formula's utility and how to apply it in practical situations.

Youtube Videos

Heron's Formula Class 9 in One Shot 🔥 | Class 9 Maths Chapter 10 Complete Lecture
Heron's Formula Class 9 in One Shot 🔥 | Class 9 Maths Chapter 10 Complete Lecture
Heron's Formula : Summary : Chapter 12 : Class 9
Heron's Formula : Summary : Chapter 12 : Class 9
Heron's Formula | One Shot | Class 9 Maths
Heron's Formula | One Shot | Class 9 Maths
Heron's Formula | Introduction | Chapter 10 | SEED 2024-2025
Heron's Formula | Introduction | Chapter 10 | SEED 2024-2025
CBSE Class 9 || Maths || Heron’s Formula || Animation || in English
CBSE Class 9 || Maths || Heron’s Formula || Animation || in English
Triangle area formula
Triangle area formula
Heron's Formula | Area of Triangle | Geometry | Math | LetsTute
Heron's Formula | Area of Triangle | Geometry | Math | LetsTute
Heron's Formula
Heron's Formula
Class 9 CBSE Mathematics - Heron’s Formula In 15 Minutes | Xylem Class 9 CBSE
Class 9 CBSE Mathematics - Heron’s Formula In 15 Minutes | Xylem Class 9 CBSE
Heron's Formula
Heron's Formula

Audio Book

Dive deep into the subject with an immersive audiobook experience.

Heron's Formula for Area of a Triangle

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

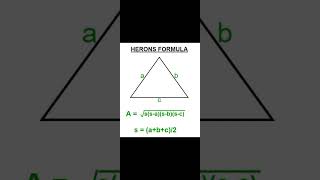
Area of a triangle with its sides as a, b and c is calculated by using Heron’ s formula, stated as

Area of triangle = ( ) ( ) ( )− − −s s a s b s c

where s = (a + b + c) / 2.

Detailed Explanation

Heron's Formula allows us to calculate the area of a triangle when we know the lengths of all three sides (denoted as a, b, and c). First, we calculate the semi-perimeter, denoted as s, which is half the sum of the lengths of the sides:

s = (a + b + c) / 2.

Once we have the semi-perimeter, we can use Heron's formula as follows:

Area = √[s × (s - a) × (s - b) × (s - c)].

This means you subtract each side length from the semi-perimeter, multiply these results together with s, and then take the square root to find the area of the triangle.

Examples & Analogies

Imagine you are trying to find the area of a plot of land shaped like a triangle. If you know the lengths of the three sides, you can use Heron's formula, kind of like a secret code that turns those side lengths into the area measurement you need, helping you understand how much grass to plant or how much space you have.

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Heron's Formula: A method for finding the area of a triangle based on its sides.

  • Semi-perimeter: Essential for calculating the area using Heron's formula.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • {'example': 'Calculate the area of a triangle with sides 40 m, 32 m, and 24 m.', 'solution': '$s = \frac{40 + 32 + 24}{2} = 48 \text{ m}, \text{then use } Area = \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{48(48-40)(48-32)(48-24)} = 384 \text{ m}^2.$'}

  • {'example': 'Find the area of an equilateral triangle with side length 10 cm.', 'solution': '$s = \frac{10 + 10 + 10}{2} = 15 \text{ cm, then } Area = \sqrt{15(15-10)(15-10)(15-10)} = \sqrt{15 \times 5 \times 5 \times 5} = \frac{25\sqrt{3}}{4} \text{ cm}^2.$'}

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • To find the area of a triangle, Heron's formula is a gem,

📖 Fascinating Stories

  • Imagine a triangle longing to be measured. One day, Heron gave it a special formula to reveal its area without needing height!

🧠 Other Memory Gems

  • Remember: SASS for Heron's Formula - S for Semi-perimeter, A for Area, S for Sides.

🎯 Super Acronyms

H.A.S. - Heron's Area through Sides.

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: Semiperimeter

    Definition:

    Half the perimeter of a triangle, calculated as $s = \frac{a + b + c}{2}$.

  • Term: Heron's Formula

    Definition:

    A formula used to calculate the area of a triangle when only the lengths of its sides are known.