7.5 - Equations of Motion

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Introduction to Equations of Motion

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Welcome class! Today, we're diving into the new section on equations of motion. Can anyone tell me why we need equations to describe motion?

Student 1
Student 1

To understand how objects move and predict their future positions!

Teacher
Teacher

Exactly! We define motion through parameters like distance, initial velocity, final velocity, acceleration, and time. Let's remember the acronym **DIVA** for Distance, Initial velocity, Velocity, and Acceleration. Now, who can explain what uniform acceleration means?

Student 2
Student 2

It means the object's speed is increasing or decreasing at a constant rate.

Teacher
Teacher

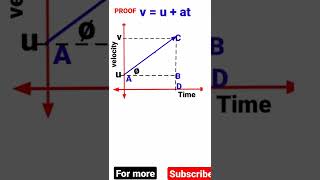
That's right! Now let's look at the first equation, v = u + at. Can anyone break down this formula?

Student 3
Student 3

It shows how our final velocity depends on initial velocity and acceleration over time!

Teacher
Teacher

Perfect! Remember, the final velocity equals the initial velocity plus the product of acceleration and time. Let's summarize today's discussion: the significance of motion, parameters involved, and the first equation.

Understanding the Second Equation of Motion

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Now let's discuss the second equation: s = ut + ½ at². What does this tell us?

Student 4
Student 4

It calculates the total distance traveled by considering initial velocity and the effect of acceleration!

Teacher
Teacher

Great observation! Here, s signifies the distance traveled. Remember the term **SAF** for Speed, Acceleration, and Final distance to recall its components. Can you think of a practical example where we might use this equation?

Student 2
Student 2

When calculating how far a car moves from a stop when it starts accelerating?

Teacher
Teacher

Exactly! It comes in handy in many real-life scenarios. Recap: we have discussed the second equation depicting how distance travelled involves initial speed and acceleration.

Exploring the Third Equation of Motion

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Let’s now analyze the third equation: v² = u² + 2as. How does this differ from the previous formulas?

Student 3
Student 3

It relates the velocities and distance directly without involving time!

Teacher
Teacher

Exactly! You can think of it as changing velocity based on acceleration and the distance covered. We can use the mnemonic **VUDAS** which stands for Velocity, Uniform acceleration, Distance, and Square. Why do you think this could be useful?

Student 1
Student 1

In situations where time isn't available, we can still understand motion!

Teacher
Teacher

Correct! And that flexibility makes this equation powerful. To summarize, v² = u² + 2as assists us in determining the relationship between distance and velocity when time isn't known.

Applications of Equations of Motion

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Now that we’ve covered all three equations, let’s ponder their applications. How can we apply these equations in engineering?

Student 4
Student 4

We can use them to design safer vehicles by calculating stopping distances and speeds.

Teacher
Teacher

Exactly! Engineers often use these equations to improve safety measures. Can anyone think of another application?

Student 2
Student 2

In sports, to analyze how fast an athlete should accelerate to reach a certain position?

Teacher
Teacher

Correct again! The applications are diverse and practical. To summarize, today's discussion revolved around real-life examples of using equations of motion.

Recap and Concept Reinforcement

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

To wrap up our unit on equations of motion, let’s briefly recap. We went through three central equations: v = u + at, s = ut + ½ at², and v² = u² + 2as. What does each signify?

Student 1
Student 1

The first shows how the velocity changes over time!

Student 2
Student 2

The second calculates the distance considering initial motion and acceleration.

Student 3
Student 3

And the third links distance and velocity without needing time.

Teacher
Teacher

Well done! Remember that understanding these equations is crucial because they apply to various real-world situations, especially in physics and engineering!

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

This section discusses the equations governing the motion of objects moving along a straight line under uniform acceleration.

Standard

The section introduces the three equations of motion, highlighting their significance in relating velocity, acceleration, and distance covered by an object. Examples and applications help elucidate how these equations are derived and used in practical scenarios.

Detailed

Detailed Summary of Equations of Motion

In this section, we explore the foundational principles of kinematics, focusing on objects in motion with uniform acceleration. Uniform acceleration means that the rate of change of velocity remains constant over time. The three critical equations that describe such motion are:
1. v = u + at
- This equation connects the final velocity (v) of an object to its initial velocity (u), acceleration (a), and the time (t) during which this acceleration occurs.
2. s = ut + ½ at²
- Here, s represents the distance moved by the object, incorporating both its initial velocity and the distance covered due to acceleration.
3. v² = u² + 2as
- This equation relates the squares of the velocities and the acceleration with the distance traveled, allowing for scenarios where time is not directly involved.

These equations are derived through graphical methods, showcasing their derivation and practical utility in real-world problems. Understanding these relationships allows for the prediction and analysis of various motion scenarios, essential for fields such as engineering and physics.

Youtube Videos

Equations of Motion (Physics)
Equations of Motion (Physics)
Motion Class 9 Physics
Motion Class 9 Physics
class 9 derivation of equation of motion |class 9 ch motion ncert acience | motion physics |
class 9 derivation of equation of motion |class 9 ch motion ncert acience | motion physics |
JEE Physics Equation of Motion Trick🤹❤️❤️#jee #iitjee #jeephysics #jeemains2024 #cbse #physicstricks
JEE Physics Equation of Motion Trick🤹❤️❤️#jee #iitjee #jeephysics #jeemains2024 #cbse #physicstricks
Equation of Motion (Non-Graphical Method) (Part I) - Chapter 7 - Motion - Science Class 9
Equation of Motion (Non-Graphical Method) (Part I) - Chapter 7 - Motion - Science Class 9
Motion Class 9
Motion Class 9
Motion Class 9 Science | NCERT Line by Line with Easy Explanation by Surya Sir
Motion Class 9 Science | NCERT Line by Line with Easy Explanation by Surya Sir
CBSE Class 9 Physics | Graphs of Motion One Shot in 90 Seconds | NCERT Class 9th Motion Chapter-8
CBSE Class 9 Physics | Graphs of Motion One Shot in 90 Seconds | NCERT Class 9th Motion Chapter-8
Equations of Motion by Graphical Method
Equations of Motion by Graphical Method
Equations of Motion Sums
Equations of Motion Sums

Audio Book

Dive deep into the subject with an immersive audiobook experience.

Introduction to Equations of Motion

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

When an object moves along a straight line with uniform acceleration, it is possible to relate its velocity, acceleration during motion and the distance covered by it in a certain time interval by a set of equations known as the equations of motion. For convenience, a set of three such equations are given below:

v = u + at (7.5)
s = ut + ½ at² (7.6)
2as = v² - u² (7.7)

Detailed Explanation

This chunk introduces the concept of motion with uniform acceleration. When an object moves straight with consistent acceleration, we can describe how its velocity changes over time and the distance it travels using specific formulas. The three equations listed are fundamental in physics, especially in mechanics. Here:
- 'v' stands for final velocity, 'u' is the initial velocity, 'a' represents acceleration, 't' is time, and 's' is the distance.
- Equation 7.5 shows how the final velocity is affected by the initial speed and acceleration over time.
- Equation 7.6 describes the relationship between distance, initial velocity, time, and acceleration.
- Equation 7.7 connects acceleration with the initial and final velocities.

Examples & Analogies

Imagine you're riding a bicycle. If you start from rest (u = 0), and pedal harder (accelerate), you will go faster and cover a distance. If you note how fast you're going at different times, you can use these equations to figure out how far you've traveled and how quickly you reached that speed.

Understanding the Equations

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

where u is the initial velocity of the object which moves with uniform acceleration a for time t, v is the final velocity, and s is the distance travelled by the object in time t. Eq. (7.5) describes the velocity-time relation and Eq. (7.6) represents the position-time relation. Eq. (7.7), which represents the relation between the position and the velocity, can be obtained from Eqs. (7.5) and (7.6) by eliminating t. These three equations can be derived by graphical method.

Detailed Explanation

In this chunk, each equation's role is clarified. Equation 7.5 focuses on how the speed of an object changes when it accelerates. Equation 7.6 shows how far the object moves over time considering its starting speed and how fast it's speeding up. Lastly, Equation 7.7 is useful because it connects speed and distance travelled without needing to consider time directly. The hint that these equations can be derived graphically suggests that visualizing motion on a graph helps understand their relationships.

Examples & Analogies

Think of a car on a road. If you press the accelerator steadily (a), the speed of the car (v) will increase from where you started (u) to a new speed. By knowing how long you've been accelerating (t), you can find out how far the car has travelled (s). If you graph these changes, it visually shows the relationship between speed and distance over time!

Examples Involving Equations of Motion

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Example 7.5: A train starting from rest attains a velocity of 72 km h–1 in 5 minutes. Assuming that the acceleration is uniform, find (i) the acceleration and (ii) the distance travelled by the train for attaining this velocity.

... Example 7.6: A car accelerates uniformly from 18 km h to 36 km h in 5 s. Calculate (i) the acceleration and (ii) the distance covered by the car in that time.

Detailed Explanation

These examples illustrate how to apply the equations of motion to real scenarios. For the train example, you start with initial speed of zero (since it's at rest) and calculate its acceleration and distance using the formulas provided. Similarly, for the car, you start with a specific speed and calculate how quickly it accelerates and how far it travels during that time. Solving these practical situations helps solidify the understanding of how the equations work in real life.

Examples & Analogies

Imagine you’re timing how fast you can run from a start line to a finish line after speeding up. You start from rest, and as you run faster, you can use the equations to compute how long it takes you to reach the end and how much ground you've covered. It's like timing a sprint and figuring out your pace!

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Equations of motion relate distance, velocity, acceleration, and time.

  • v = u + at connects final velocity to initial velocity and acceleration.

  • s = ut + ½ at² calculates distance considering both initial velocity and acceleration.

  • v² = u² + 2as links velocities and distance traveled without time.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • Example scenario: A car accelerates uniformly from rest at 2 m/s² for 5 seconds. Using the equations, we can calculate its final velocity and distance covered.

  • Practical application: Engineers use equations of motion to calculate stopping distances for vehicles based on given acceleration rates.

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • To find a car's final speed, v = u + at is all you need!

📖 Fascinating Stories

  • A bus starts its journey, accelerating from rest, measuring time, and distance, it travels on its quest.

🧠 Other Memory Gems

  • Use the acronym SVA for Speed, Velocity, and Acceleration to remember key terms in motion.

🎯 Super Acronyms

Remember 'SUVAT'

  • S: for Distance
  • U: for Initial Velocity
  • V: for Final Velocity
  • A: for Acceleration
  • T: for Time.

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: Uniform Acceleration

    Definition:

    Acceleration that remains constant over time.

  • Term: Initial Velocity (u)

    Definition:

    The velocity of an object at the start of the time interval.

  • Term: Final Velocity (v)

    Definition:

    The velocity of an object at the end of the time interval.

  • Term: Distance (s)

    Definition:

    The total path length covered by an object during its motion.

  • Term: Acceleration (a)

    Definition:

    The rate of change of velocity of an object, expressed in units such as m/s².