Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Work
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will delve into the concept of 'work' in physics. When we say someone is 'working hard,' it may not mean they are doing physical work in a scientific sense. Can anyone tell me what we mean by work in science?
Isn't work just anything that requires effort, like doing homework or cleaning?
That's a common understanding! However, in science, we specifically mean that work is done when a force causes displacement of an object. So, if you push a box and it moves, thatβs work. Can anyone think of a situation where you exert force but no work is done?
When I push against a wall and it doesn't move at all!
Exactly! No displacement means no work done. This is a crucial distinction. Let's remember it as 'Force x Displacement = Work' or W = F Γ d.
So if I lift a heavy box, Iβm doing work because it moves upwards?
Right! The force exerted while lifting the box multiplied by the height it moves gives us the work done. Remember, direction matters!
Exploring Power
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we understand work, let's talk about power. What is power?
Is it about doing work faster?
Correct! Power is defined as the rate at which work is done. Mathematically, it's given by the equation P = W/t, where P is power, W is work, and t is time. Can anyone give me an example?
How about climbing stairs? If two people climb the same height, but one is faster, they have more power!
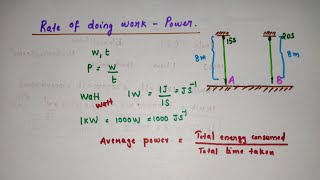
Great example! The faster climber does the same amount of work in less time, which means higher power. If Girl A climbs 8 m in 20 seconds and Girl B takes 50 seconds, we can calculate their power outputs to see who is more powerful.
So if I want more power when cycling, I just need to pedal faster?
Absolutely! But remember, itβs not just about speed; efficiency in doing work is part of it. Letβs summarize this as 'Power = Work/Time'.
Practical Application of Power
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
To further our understanding, let's calculate some examples! First, if Girl A lifts a 400 N load 8 m in 20 seconds, how do we find her power?
Weβd find the work done using W = F Γ d, so W = 400 N Γ 8 m!
Exactly! Whatβs that equal?
3200 J! Then we divide by the time, which is 20 s.
Good job! So, how much power does she exert?
I think itβs 160 W.
Correct! Now, how about Girl B, who takes 50 seconds? Letβs see how her output compares.
So she'd have the same work done, but divided by 50 seconds.
Correct! This allows us to see how efficiency can differ even when the same work is accomplished. Remember, it's critical to compute both work and power to understand performance!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the scientific definition of work, highlighting how it differs from everyday language. The importance of displacement in defining work is emphasized. Additionally, we discuss power as the rate of doing work, illustrated through examples and calculations, and examine how different agents may perform work at varying rates.
Detailed
In physics, 'work' is defined as the energy transferred when a force displaces an object. The relationship between work and energy is critical for understanding physical processes. This section also introduces the concept of power, which is defined as the rate at which work is done. Power can vary widely between different agents doing the same task, highlighting the efficiency and effectiveness of energy transfer. Key examples included involve calculating work done by students performing physical activities and engines operating at different efficiencies. Understanding these concepts is crucial as they lay the foundational principles of mechanics and energy.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Variation in Work Rate
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This means that the agent may be doing work at different rates at different intervals of time.
Detailed Explanation
Not all individuals or machines exert energy at the same rate when performing work. The rate of work done can vary depending on factors like the efficiency of the individual or the power of the machine. This variability is important to understand how work and power are related.
Examples & Analogies
Imagine two runners in a race. One is fast and finishes the race quickly, while the other takes longer. Both have completed the race, but the first runner did it at a higher rate of work. This difference showcases how the time taken to complete a task affects the rate of doing work.
Activity Illustration with Two Girls
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example 10.7 Two girls, each of weight 400 N climb up a rope through a height of 8 m. We name one of the girls A and the other B. Girl A takes 20 s while B takes 50 s to accomplish this task. What is the work done by each?
Detailed Explanation
In this scenario, both girls perform the same amount of work because they lift the same weight to the same height. The work done can be calculated using the formula Work = Weight Γ Height. However, the power exerted by each girl differs because power is defined as work done per unit of time. Therefore, even though they do the same work, girl A, who takes less time, will have a higher power output than girl B.
Examples & Analogies
Think of two people filling a bucket with water from a well. One person scoops quickly and fills the bucket in a minute, while the other takes five minutes to do the same. Both fill the same bucket with the same amount of water, but the first person did it at a higher rate, demonstrating a greater power output.
Calculating Power Output
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Power is calculated using the formula: P = Work done / Time taken.
Detailed Explanation
When we want to understand how quickly work is done, we use the concept of power. Power quantifies the rate of doing work and is expressed in watts (W). For instance, if one girl expends the same amount of work in a shorter time, her power output will be greater. Knowing how to calculate power gives us a better understanding of efficiency in various activities.
Examples & Analogies
Consider a blender. If it processes ingredients quickly, it's efficient and you can prepare meals faster. The speed at which your blender operates reflects its power output: a faster blender has a higher power rating than a slower one.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Work: Defined as force applied over a distance causing displacement.
-
Power: Defined as the rate of doing work; measured in watts (1 W = 1 J/s).
-
Displacement: Essential for work to be done; must occur in the direction of the force.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Lifting a box vertically from the ground constitutes work due to force and displacement.
-
Two girls doing the same work (lifting weight) in different times can have different power outputs.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
When force and distance come to play, work gets done in a measurable way.
π Fascinating Stories
-
Once, in a big field, two workers named A and B tried to lift the same heavy rock. A took longer to do it but was tired, while B did it faster and got to eat first. This taught them that work is important, but power shows who is faster!
π§ Other Memory Gems
-
F-D-W: Force times Distance equals Work done.
π― Super Acronyms
P = W/T, Power equals Work divided by Time.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Work
Definition:
The energy transferred when a force causes displacement of an object.
-
Term: Power
Definition:
The rate at which work is done or energy is transferred, measured in watts.
-
Term: Displacement
Definition:
The distance and direction an object has moved from its initial position.