Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Matrix Representation of Points
Unlock Audio Lesson
Today we're going to discuss how we represent points in both 2D and 3D using matrices. What do you think a point in 2D looks like?
I think it could be some coordinates like x and y?
Exactly! We represent a point in 2D as a column vector, like [x, y]. Now, how do you think we represent a point in 3D?
Maybe we add a z-coordinate?
Yes, in 3D, it's represented as [x, y, z]. Remember this as 'XYZ for 3D, XY for 2D'. It’s crucial for our transformations!
Can we use these vectors for manipulating shapes?
Absolutely! We can transform these points using matrices, which is critical in computer-aided design. Let's summarize the key idea: Points are represented as vectors in both dimensions.
Lines in 2D and 3D
Unlock Audio Lesson
Moving on to lines, in 2D we can represent a line with an equation, like ax + by + c = 0. How might we write that as a vector?
Wouldn't it look similar to the point representation?
Yes, you're right! It's related but used differently. In 3D, we describe a line parametrically with two points or a point along with a direction vector. Can someone explain what a direction vector would be like?
It should tell us which way the line is going?
Exactly! A direction vector gives us that direction. Remember, for lines we can think of 'LEFT or RIGHT for direction'.
What about the plane representation?
Good question! Let's bring that up in our next session.
Planes in 3D
Unlock Audio Lesson
Now, let’s talk about planes. In 3D, a plane can be represented with an equation like ax + by + cz + d = 0. How do we visualize this?
Is it like how we visualize a flat surface?
Exactly! The coefficients a, b, c describe the plane’s orientation. Can anyone think of how we might represent this with a matrix?
Maybe as a vector, similar to lines?
Yes! It allows us to perform transformations, very essential in CAD. Let's summarize that planes give us a flat surface in 3D represented by equations.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
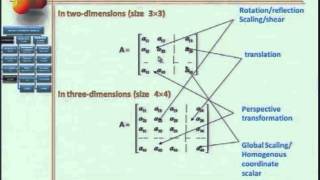
The section covers how points are represented in column vectors, the equations of lines in both dimensions, and the representation of planes in 3D. It emphasizes the importance of understanding these representations for effective transformations in computer-aided design.
Detailed
Matrix Representation of Points, Lines, and Planes
This section provides a comprehensive overview of how points, lines, and planes can be represented mathematically using matrices, which are essential for transformations in computer graphics and CAD applications.
Points
In 2D, a point can be represented as a column vector
[x, y], while in 3D, it extends to
[x, y, z]. The use of column vectors facilitates the application of transformations through matrix multiplication.
Lines
A line in 2D can be described by the equation ax + by + c = 0, and its corresponding vector representation can be used to facilitate geometric transformations. For 3D, a line can be defined parametrically utilizing two points or a point with a direction vector.
Planes
In three-dimensional space, planes are represented either by the equation ax + by + cz + d = 0 or through vector representation, which aids in understanding how to manipulate planar geometry in CAD applications.
Each of these representations is foundational for conducting 2D and 3D transformations, which are critical in computer-aided design, animation, and a variety of graphics applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Matrix Representation of Points
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A point in 2D can be represented as a column vector:
In 3D:
Detailed Explanation
In computer graphics and CAD, a point in 2D space can be represented using a column vector, typically as follows:
- A 2D point (x, y) is represented as a vector:
\[ \begin{bmatrix} x \ y \end{bmatrix} \]
Given the context, in 3D space, we can extend this by adding a z-coordinate, leading to:
- A 3D point (x, y, z) is represented as:
\[ \begin{bmatrix} x \ y \ z \end{bmatrix} \]
Examples & Analogies
Imagine you are giving directions in a city. You can specify your location using coordinates.
In a flat, 2D map, you'd say something like 'I am at (3, 5)', which indicates the point on the map. In a 3D space, think of a video game where your character moves, and each coordinate represents a position in space, such as 'I am at (3, 5, 7)', representing your location in a room.
Matrix Representation of Lines
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In 2D, a line with equation $ ax + by + c = 0 $ can be represented as the vector.
In 3D, a line may be defined parametrically using two points or a point and a direction vector.
Detailed Explanation
In 2D, lines can be expressed with a standard equation such as $ ax + by + c = 0 $. This can be transformed into a vector representation.
- The coefficients (a, b, c) can create a vector that represents the direction of the line.
For a line in 3D, we can use two points (P1 and P2) or a point and a direction vector. The direction vector indicates how the line extends through space.
Examples & Analogies
Visualize two friends standing on a straight path. You can connect their positions with a line—their locations are points on this line. Similarly, if these friends decide to go in a specific direction, you can represent their movement by a direction vector showing which way they are headed.
Matrix Representation of Planes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In 3D, a plane is represented as $ ax + by + cz + d = 0 $ or as the vector.
Detailed Explanation
In 3D graphics, a plane can be represented mathematically by an equation known as the plane equation, written as:
- $ ax + by + cz + d = 0 $. Here, (a, b, c) represent the normal vector of the plane, determining its orientation in space, and d is a constant that affects the position of the plane.
Alternatively, we can also use a vector to describe the plane’s parameters, relating to how we represent geometric data in CAD applications.
Examples & Analogies
Think of a sheet of paper placed in a room. The paper takes up a flat surface, which can be defined using the plane equation. The normal vector is like an arrow sticking straight out from the center of the paper — it tells you which direction is 'up' relative to the paper, helping to understand its orientation in 3D space.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Matrix Representation: Points can be represented as column vectors; lines and planes are defined parametrically or through equations.
-
Affine Transformations: Understanding points, lines, and planes helps in using transformations in CAD.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A point in 2D: [3, 4], represents the coordinates on a graph.
-
A line in 3D can be represented parametrically as: L(t) = P + tD where P is a point on the line and D is the direction vector.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In two dimensions, a point stands tall, with x and y at the core of it all.
📖 Fascinating Stories
-
Imagine a sailor at sea, using a compass to find their way; the direction vector is like the compass needle, guiding the line on its journey.
🧠 Other Memory Gems
-
To remember points, lines, and planes, think: "Points are Vectors, Lines are Ranges, Planes are Equations!"
🎯 Super Acronyms
PLP
- Points
- Lines
- Planes – the essential geometric trio.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Point
Definition:
A specific location in 2D or 3D represented as a vector.
-
Term: Line
Definition:
A straight path that extends infinitely in both directions, represented by an equation in 2D or parametrically in 3D.
-
Term: Plane
Definition:
A flat, two-dimensional surface that extends infinitely in 3D space, represented by a linear equation.
-
Term: Matrix
Definition:
A rectangular array of numbers used to represent points, lines, and transformations.